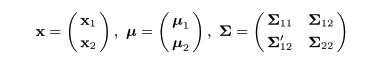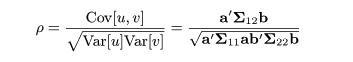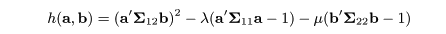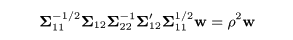非計量的MDSによる4次元までのスコアの組み合わせと
主成分分析による第3主成分までのスコアの組み合わせの最大の相関を求める
正順相関分析を適応した.
第1正順相関の値が0.9287という高い値が得られた.第1正順変量の係数と
主成分の固有ベクトルに対する正順変量の係数で重みづけを行ったSD法評価尺度
係数が左の表である.これをみると,非計量的MDSの第1,第2,第4軸を合成した成分
は,第2主成分をメインに第1主成分を半分程度加えた成分に対応している.
この合成主成分をSD法評価尺度でみると,「4:退屈」,「7:整然」,「8:緑少ない」,
「9:広々」が正で,「5:複雑」が負の
寄与が大きくなっている.この合成
得点が高い景観は,「単純で緑少なく,広々と整然
としているが退屈」といった印象を与える.また,このような評価軸は,類似性の
基準の中に埋め込まれていることが示された.
評価軸間相関行列
gardenuse.dfr <- read.csv("gardenuse.csv")
ord <- order(gardenuse.dfr$usage,gardenuse.dfr$gardenNo)
g.mds.mat <- gmet.iso.mat[ord,][39:78,]
cor(cbind(g.mds.mat, gq.corresp$rscore, gjpm.prin.out$x[,1:3]))
非計量的MDSによる4次元庭景観写真座標行列(gmet.iso.mat)から40景観を抜き出したものを
g.mds.mat とし,数量化3類による4次元写真座標行列 gq.corresp\$rscore と
主成分分析による3次元写真座標行列 gjpm.prin.out\$x[,1:3] との相関の計算.
非計量的MDS解と主成分分析解との正順相関分析(cancor())
library(mva)
canmp.out <- cancor(scale(g.mds.mat), scale(gjpm.prin.out$x[,1:3]))
第1正順変量の係数と評価尺度に対する係数
mds.coef <- sqrt(39)*canmp.out$xcoef[,1]
pc.coef <- sqrt(39)*canmp.out$ycoef[,1]
sd.coef <- gjpm.prin.out$rotation[,1:3] %*% pc.coef