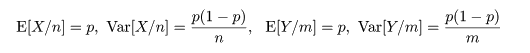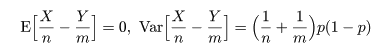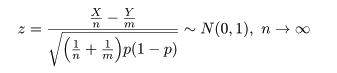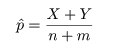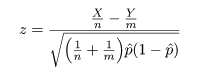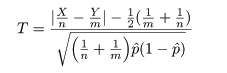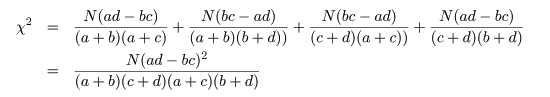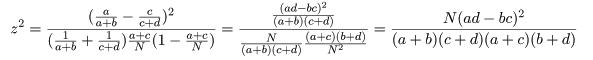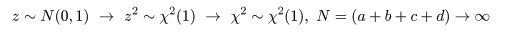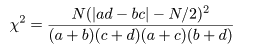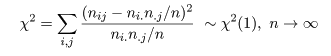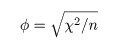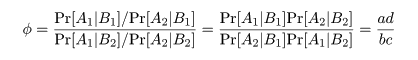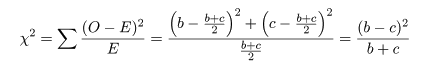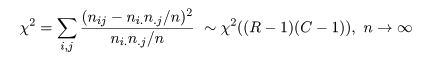統計特論２

東京大学大学院農学生命科学研究科　大森宏

この講義の目的

　統計解析ソフトＲを用いて，多変量解析手法の理論と解釈を学ぶ

０．前期レポート

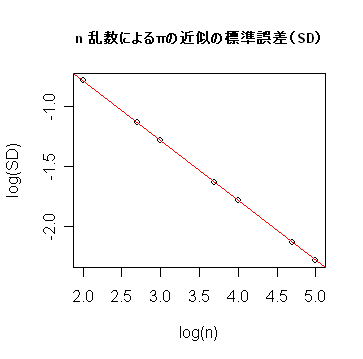
レポート１：乱数点の個数 n を大きくしたとき，πの近似誤差の大きさの減少の程度を n のオーダーで表せ．

**# レポート１の R スクリプト**
pi.f <- function(n){	# 乱数点の個数 n のとき，πの近似の標準誤差を出力する関数
N <- 10000	# 点セット列の長さ
#n <- 1000	# 乱数点の個数
pi <- NULL	# pi の定義
for(i in 1:N){	# N 回の繰り返し
x <- runif(n, -1, 1)	# (-1, 1) の範囲の一様乱数 n 個生成
y <- runif(n, -1, 1)	#
r <- x^2 + y^2	# 原点からの距離の２乗
pi <- c(pi, 4*length(r[r<1])/n)	# πの近似値ベクトル
}	#
m = mean(pi)	# 近似値の平均
s = sd(pi)	# 近似値の標準偏差
m	# 平均の表示
return(s)	# 標準偏差の表示
}	#
#	#
nn <- c(100,500,1000,5000,10000)	# n の値のベクトル(50000, 100000をカット)
y <- NULL	# 標準誤差を格納するベクトル
for(i in 1:length(nn))	#
y <- c(y, pi.f(nn[i]))	#
#	#
plot(nn,y, xlab="乱数の個数 n",ylab="標準誤差 SD")	# 普通にプロット
plot(log10(nn),log10(y), xlab="log(n)",ylab="log(SD)")	# 両対数でのプロット
z <- lm(log10(y) ~ log10(nn))	# 直線回帰
abline(z, col="red")	# 回帰直線の表示
title(main="n 乱数によるπの近似の標準誤差（SD）", cex.main=0.8)
summary(z)	# 回帰分析結果

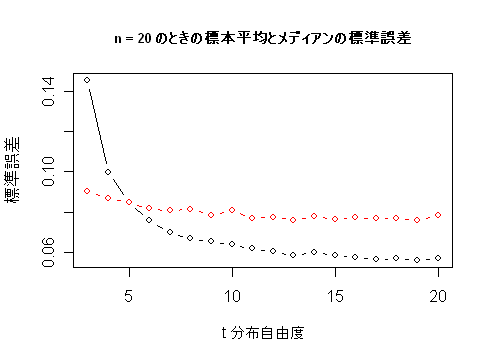
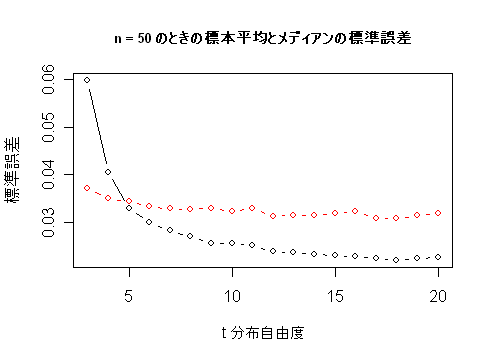
レポート２：メディアンと標本平均の分散が同程度になる t 分布の自由度を求めよ．

**# レポート２の R スクリプト**
med.f <- function(n, m){	# サンプルサイズ n，t 分布自由度 m，
N <- 10000	# シミュレーション回数
#m <- 2	# t 分布自由度
#n <- 20	# サンプルサイズ
y1 <- NULL	#
y2 <- NULL	#
for(i in 1:N){	#
x <- rt(n, df=m)	# t 分布乱数 n 個
y1 <- c(y1, mean(x))	# 標本平均列
y2 <- c(y2, median(x))	# メディアン列
}	#
m1 <- mean(y1); m2 <- mean(y2)	# 標本平均とメディアンの平均
s1 <- var(y1); s2 <- var(y2)	# 標本平均とメディアンの分散
s2/s1	# 分散比
sqrt(s1)	# 標本平均の標準誤差
sqrt(s2)	# メディアンの標準誤差
ss <- c(s1,s2)	# 標準誤差ベクトル
return(ss)	#
}	#
res20 <- NULL	# 標準誤差行列
for(i in 1:20)	#
res20<- rbind(res20,med.f(20, i))	# n = 20
x <- 3:20	#
plot(x, res20[3:20,1], type="b", xlab="t 分布自由度", ylab="標準誤差")
points(x,res20[3:20,2], type="b", col="red")	#
title(main="n = 20 のときの標本平均とメディアンの標準誤差", cex.main=0.8)
res50 <- NULL	#
for(i in 1:20)	#
res50<- rbind(res50,med.f(50, i))	# n = 50

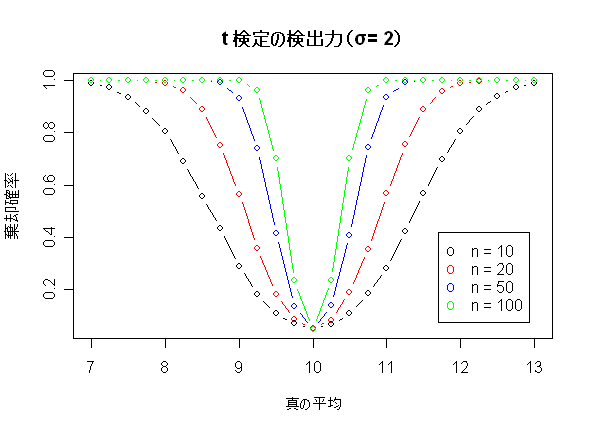
レポート３： t 検定の検出力関数（帰無仮説の母平均 μ₀ = 10 ）．

**# レポート３の R スクリプト**
power.f <- function(n,m){	#サンプルサイズ n，t 分布自由度 m
N <- 10000	# シミュレーション回数
#n <- 10	# サンプルサイズ
n1 <- rnorm(N*n, mean=m, sd=2)	# N(10, 4) から大きさ n の標本を N 回シミュレーション
n1.mat <- matrix(data=n1, ncol=n)	# データ行列
n1.mean <- apply(n1.mat, 1, mean)	# 各サンプルの平均
n1.var <- apply(n1.mat, 1, var)	# 各サンプルの分散
n1.var3 <- n1.var/n	# 各標本平均の分散
n1.td <- (n1.mean - 10)/sqrt(n1.var3)	# 各サンプルの t 値
mean(n1.td)	# t 値の平均
sd(n1.td)	# t 値の標準偏差
mt <- ceiling(max(abs(n1.td)))	# t 値の絶対値の最大値
xq1 <- qt(0.025, df = (n-1))	# t(9) の 2.5% 点
xq2 <- qt(0.975, df = (n-1))	# t(9) の 97.5% 点
ns <- length( n1.td[abs(n1.td) > xq2])	# 5% 検定で有意となった個数
return(ns/N)	# 棄却確率
}	#
x <- seq(8.5,11.5,by=0.25)	# 真の平均（区間を短くした）
n <- 10	# サンプルサイズ 10
y <- NULL	#
for(i in 1:length(x))	#
y <- c(y, power.f(n,x[i]))	# 棄却確率ベクトル
n <- 20	# サンプルサイズ 20
y2 <- NULL	#
for(i in 1:length(x))	#
y2 <- c(y2, power.f(n,x[i]))	#
n <- 50	# サンプルサイズ 50
y3 <- NULL	#
for(i in 1:length(x))	#
y3 <- c(y3, power.f(n,x[i]))	#
n <- 100	# サンプルサイズ 100
y4 <- NULL	#
for(i in 1:length(x))	#
y4 <- c(y4, power.f(n,x[i]))	#
plot(x,y, type="b", xlab="真の平均", ylab="棄却確率", ylim=c(0,1))
points(x,y2, type="b",col="red")	#
points(x,y3, type="b",col="blue")	#
points(x,y4, type="b",col="green")	#
title(main="t 検定の検出力（σ= 2）")	#
legend(11.7,0.42, c("n = 10","n = 20","n = 50","n = 100"),pch="o",col=c("black","red","blue","green"))

１．分割表の解析

　対象をいくつかの質的変数でカテゴリーに分けることはよく行われる．たとえば，社会科学データでは，人間集団を性別，年齢，職業，趣味などで分類する．ここで興味がもたれるのは，たとえば，被験者の社会的属性（性別，年齢，学歴など）により，ある問題に対する意見や趣味嗜好が異なっているかどうか，である．これを統計学的に書き直すと，属性ごとで意見分布が同じかどうかを検定することに帰着する．
　この問題は，統計特論３で考えた，成功確率（比率）の検定からの拡張と捉えることができる．

成功確率（比率）の同等性の近似検定

　成功確率 p_x のベルヌイ試行を n 回行ったときの成功回数を X，成功確率 p_y のベルヌイ試行を m 回行ったときの成功回数を Y とする．このとき，２つの成功確率が等しいかどうか，すなわち，

帰無仮説，H₀： p_x ＝ p_y，対立仮説，H₁： p_x ≠ p_y，

の検定を考える．帰無仮説のもとでは，p_x = p_y = p とおけるので， p_x の推定量である X/n と p_y の推定量である Y/m の平均と分散は，それぞれ，

となる．これより，X/n - Y/m の帰無仮説のもとで平均と分散は，

となるので，これをその平均を引いて標準偏差で割って標準化した z は，

のように漸近的に標準正規分布に従う．
　ところで，帰無仮説のもとでの成功確率 p は，X と Y をこみにして，

と推定されるので，これを z に代入すれば，

となり，T = |z| を検定統計量にして，たとえば，T ＞ 1.96 のとき帰無仮説を棄却すれば，近似的な有意水準 5％の検定が行える．
　なお，連続性の補正を入れた検定統計量は，

となる．

勝率の同等性の検定
　前節では，A と B で将棋を 10 試合行い，A が 7 勝 3 敗の成績だったときに，A と B で将棋の強さに違いがあると言えるかの検定を行った．続いて， A と B で囲碁を 10 試合行い，A が 4 勝 6 敗の成績であったとする．このとき， A の B に対する将棋の強さと囲碁の強さとで違いがあるかの検定を行う．帰無仮説は，

H₀：A の B に対する将棋の勝率＝ A の B に対する囲碁の勝率

である．

# 勝率同等性検定の R スクリプト
r <- c(7, 4) # A の将棋の勝数と囲碁の勝数　
n <- c(10, 10) # 将棋の試合回数と囲碁の試合回数　
prop.test(r, n, correct=F) # 比率の同等性検定（連続性の補正なし）　
prop.test(r, n) # 比率の同等性検定（連続性補正）　

**# 勝率同等性検定の R スクリプト**
r <- c(7, 4)	# A の将棋の勝数と囲碁の勝数
n <- c(10, 10)	# 将棋の試合回数と囲碁の試合回数
prop.test(r, n, correct=F)	# 比率の同等性検定（連続性の補正なし）
prop.test(r, n)	# 比率の同等性検定（連続性補正）

課題：勝敗の比率はそのままで，試行回数を増やして（n = 30）同様な検定を行え．

２×２分割表

　上で述べた比率の同等性の検定は，別の表現ができる．すなわち，成功確率 p_x の試行 X では a 回成功し， b 回失敗したが，別の成功確率 p_y 試行 Y では c 回成功，d 回失敗であったとする．このとき，試行 X と試行 Y で成功確率が等しいという，

帰無仮説，H₀： p_x ＝ p_y，対立仮説，H₁： p_x ≠ p_y，

の検定を考える．
　このようなデータは，

2 × 2 分割表データ
　　成　功　　失　敗　　計　

　試行 X　 a b 　a + b　

　試行 Y　 c d 　c + d

　計　 a + c b + d N

**2 × 2 分割表データ**
	成　功	失　敗	計
試行 X	a	b	a + b
試行 Y	c	d	c + d
計	a + c	b + d	N

とまとめられる．ただし，N = a + b + c + d，である．これを２×２分割表という．各試行の成功回数と失敗回数を記録した部分をセル，その外側の「計」に対応する部分を周辺度数という．
　周辺度数を固定したときに，帰無仮説のもとでの各セル期待度数は，

帰無仮説のもとでの期待度数
　　成　功　　失　敗　

　試行 X　　(a + b)(a + c)/N　　(a + b)(b + d)/N　

　試行 Y　　(c + d)(a + c)/N 　(c + d)(b + d)/N

**帰無仮説のもとでの期待度数**
	成　功	失　敗
試行 X	(a + b)(a + c)/N	(a + b)(b + d)/N
試行 Y	(c + d)(a + c)/N	(c + d)(b + d)/N

となる．ここで，ピアソン（Pearson）のχ² 値，

を計算する．連続性の補正を入れると，

である．このとき，

Na - (a + b)(a + c) = (a + b + c + d)a - (a² + ab + ac + bc) = ad - bc

という関係を利用すると，２×２分割表の χ² 値は，

と計算される．
　ところで，比率の同等性検定の z において，X = a，Y = c，n = a + b，m = c + d， m + n = N，とおきかえると，

となり，z² 値が χ² 値と同じであることがわかる．これより，

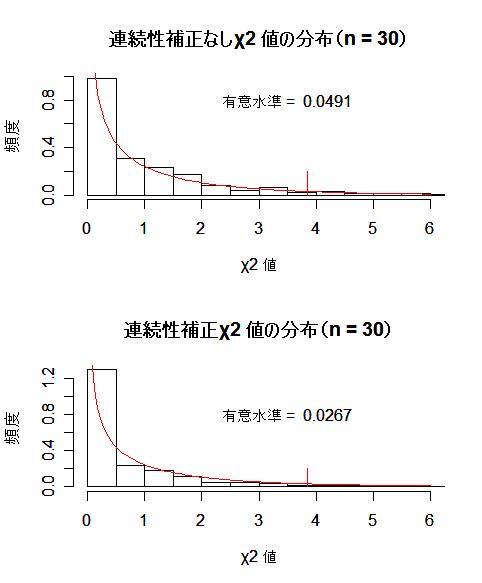
と分布するので，自由度 1 の χ² 分布を利用して，成功確率の同等性の検定を行うことができる．　また，χ² 値に連続性の補正を行うときは，

とする．

勝率同等性の χ² 検定

# 勝率同等性ピアソン χ² 検定の R スクリプト
x <- matrix(c(7, 3, 4, 6), nc=2, byrow=T) # A の将棋の勝ち負け数と囲碁の勝ち負け数の行列　
shogi <- c(7, 3) # A の将棋の勝ち負け数　
igo <- c(4, 6) # A の囲碁の勝ち負け数　
x <- rbind(shogi, igo) # 行連結による行列化　
chisq.test(x, correct=F) # 勝率同等性 χ² 検定（連続性の補正なし）　
chisq.test(x) # 勝率同等性 χ² 検定（連続性の補正）　

**# 勝率同等性ピアソン χ² 検定の R スクリプト**
x <- matrix(c(7, 3, 4, 6), nc=2, byrow=T)	# A の将棋の勝ち負け数と囲碁の勝ち負け数の行列
shogi <- c(7, 3)	# A の将棋の勝ち負け数
igo <- c(4, 6)	# A の囲碁の勝ち負け数
x <- rbind(shogi, igo)	# 行連結による行列化
chisq.test(x, correct=F)	# 勝率同等性 χ² 検定（連続性の補正なし）
chisq.test(x)	# 勝率同等性 χ² 検定（連続性の補正）

課題：勝敗の比率はそのままで，試行回数を増やして（n = 30）同様な検定を行え．

課題：ビデオリサーチ社のデータによると，関西地区において，NHK 大河ドラマ07年の「風林火山」の初回視聴率は16.2％であったが，08年の「篤姫」の初回視聴率は19.8％であった．調査対象者がどちらも600名であったとすると，関西地区で大河ドラマの人気に変化があったかどうか，検定せよ．
　なお，関東地区では「風林火山」の初回視聴率は21.3％で，「篤姫」の初回視聴率は20.3％であった．

イエーツ（Yates）の連続性の補正の効果
　χ² 検定ではイエーツの連続性補正を行った方が χ² 分布への近似がよいとされている．R でもデフォルトでは連続性の補正を行うことになっていて，連続性の補正をはずすには，そのように指定しなければならない．
　補正の効果をシミュレーションでみてみよう．成功確率がどちらも p = 0.4 として，n = 30 の二項分布乱数を２回発生させると 2 × 2 分割表ができ，χ² 値が計算される．これを N = 10000 回繰り返してその分布をみればよい．
　特に問題となるのは，帰無仮説が棄却される（第１種の過誤）確率である．これが名目の 5％より大きな検定は危険（有意になりやすい）であり，推奨されない．また，5％よりかなり小さい検定は保守的（conservative）であり，検出力が悪くなると考えられる．よって，5％を超えず，かなり近い検定が望ましい．
　なお，1％検定の近似のよさをみるためには N をもう一桁増やし，N = 100000 とした方がよい．
　結果をみると，このケース（成功確率が真ん中辺でサンプルサイズも比較的大きい）では，連続性の補正は必要ないと思われる．

# 連続性補正の効果の R スクリプト
N <- 10000 # シミュレーション回数　
m <- 30 # n = 30　
y <- NULL # 　
for(i in 1:N){ # 　
x <- rbinom(2, m, p=0.4) # n = 30，p = 0.4 の二項乱数を２回発生　
if(sum(x)==0 || sum(x)==2*m) # 成功回数が両方とも 0 のとき　
xx <- matrix(c(x[1]+0.5,m-x[1]+0.5,x[2]+0.5,m-x[2]+0.5), nc=2, byrow=T) # セルすべてに 0.5 を加える　
else # 　
xx <- matrix(c(x[1],m-x[1],x[2],m-x[2]), nc=2, byrow=T) # 行列化　
y1 <-chisq.test(xx, correct=F)$statistic # 連続性補正なし χ² 値　
y2 <- chisq.test(xx)$statistic # 連続性補正 χ² 値　
y <- rbind(y, c(y1, y2)) # 　
} # シミュレーション終わり　
my <- ceiling(max(y)) # χ² 値の最大値を超えない最小の整数
op <- par(mfrow = c(2, 1)) # 縦２つのグラフ　
y0 <- y[,1] # 　
hist(y0, breaks=seq(0,my,by=0.5),freq=FALSE,xlim=c(0,6),xlab="χ2 値",ylab="頻度",main="")
x <- seq(0,6, by=0.1) # 　
curve(dchisq(x, 1), 0, 6, add=T, col=2) # 自由度 1 の χ² 分布　
title(main="連続性補正なしχ2 値の分布（n = 30）") # 　
q0 <- qchisq(0.95,df=1) # 自由度 1 の χ² 分布 95％点　
pv <- length(y0[y0>q0])/N # q0 を超えた頻度（第１種の過誤）　
s <- paste("有意水準 = ", pv) # 　
text(3.5,0.8, s) # 　
segments(q0,0, q0,0.2, col="red") # 　
y0 <- y[,2] # 　
hist(y0, breaks=seq(0,my,by=0.5),freq=FALSE,xlim=c(0,6),xlab="χ2 値",ylab="頻度",main="")
x <- seq(0,6, by=0.1) # 　
curve(dchisq(x, 1), 0, 6, add=T, col=2) # 　
title(main="連続性補正χ2 値の分布（n = 30）") # 　
q0 <- qchisq(0.95,df=1) # 　
pv <- length(y0[y0>q0])/N # 　
s <- paste("有意水準 = ", pv) # 　
text(3.5,0.8, s) # 　
segments(q0,0, q0,0.2, col="red") # 　
par(op) # 　

**# 連続性補正の効果の R スクリプト**
N <- 10000	# シミュレーション回数
m <- 30	# n = 30
y <- NULL	#
for(i in 1:N){	#
x <- rbinom(2, m, p=0.4)	# n = 30，p = 0.4 の二項乱数を２回発生
if(sum(x)==0 \|\| sum(x)==2*m)	# 成功回数が両方とも 0 のとき
xx <- matrix(c(x[1]+0.5,m-x[1]+0.5,x[2]+0.5,m-x[2]+0.5), nc=2, byrow=T)	# セルすべてに 0.5 を加える
else	#
xx <- matrix(c(x[1],m-x[1],x[2],m-x[2]), nc=2, byrow=T)	# 行列化
y1 <-chisq.test(xx, correct=F)$statistic	# 連続性補正なし χ² 値
y2 <- chisq.test(xx)$statistic	# 連続性補正 χ² 値
y <- rbind(y, c(y1, y2))	#
}	# シミュレーション終わり
my <- ceiling(max(y))	# χ² 値の最大値を超えない最小の整数
op <- par(mfrow = c(2, 1))	# 縦２つのグラフ
y0 <- y[,1]	#
hist(y0, breaks=seq(0,my,by=0.5),freq=FALSE,xlim=c(0,6),xlab="χ2 値",ylab="頻度",main="")
x <- seq(0,6, by=0.1)	#
curve(dchisq(x, 1), 0, 6, add=T, col=2)	# 自由度 1 の χ² 分布
title(main="連続性補正なしχ2 値の分布（n = 30）")	#
q0 <- qchisq(0.95,df=1)	# 自由度 1 の χ² 分布 95％点
pv <- length(y0[y0>q0])/N	# q0 を超えた頻度（第１種の過誤）
s <- paste("有意水準 = ", pv)	#
text(3.5,0.8, s)	#
segments(q0,0, q0,0.2, col="red")	#
y0 <- y[,2]	#
hist(y0, breaks=seq(0,my,by=0.5),freq=FALSE,xlim=c(0,6),xlab="χ2 値",ylab="頻度",main="")
x <- seq(0,6, by=0.1)	#
curve(dchisq(x, 1), 0, 6, add=T, col=2)	#
title(main="連続性補正χ2 値の分布（n = 30）")	#
q0 <- qchisq(0.95,df=1)	#
pv <- length(y0[y0>q0])/N	#
s <- paste("有意水準 = ", pv)	#
text(3.5,0.8, s)	#
segments(q0,0, q0,0.2, col="red")	#
par(op)	#

課題： n = 10 回の試行のときの連続性補正の効果を調べよ．また，成功確率が比較的小さい，たとえば，p = 0.1，のときの連続性補正の効果を調べよ．このような時は，n = 50 ぐらいは必要だろう．

Fisher の直接確率法

　試行回数が少ないときは，各セルの期待度数が小さくなるので，近似の精度はよくない．2×2 分割表では，一般に期待度数が 5 以下のセルがあると χ² 検定は適当でないと言われている．このようなときは，周辺度数を固定して，データの表が得られる確率より小さな場合をすべて足し合わせて有意確率（p 値）を計算する．
　前節の囲碁と将棋の例で説明する．データを 2 × 2 分割表でまとめると以下のようになる．

将棋と囲碁 2 × 2 分割表
　　勝　ち　　負　け　　計　場合の数

　将　棋　 7 3 　10　 ₁₀C₇

　囲　碁　 4 6 　10 ₁₀C₄

　計　 11 9 　20　 ₂₀C₁₁

**将棋と囲碁 2 × 2 分割表**
	勝　ち	負　け	計	場合の数
将　棋	7	3	10	₁₀C₇
囲　碁	4	6	10	₁₀C₄
計	11	9	20	₂₀C₁₁

上の表で，勝ち負けがまったくランダムに起こったとすると，この表ができる確率は，

p = ₁₀C₇×₁₀C₄ /₂₀C₁₁ = 0.15004

となる．　次に，周辺度数を固定した場合できる可能性のある表をすべて数えあげ，勝敗がランダムなときの表が生成する確率を計算すると以下のようになる．

パターン１勝ち負け計場合の数

将　棋 8 2 10 ₁₀C₈

囲　碁 3 7 10 ₁₀C₃

計 11 9 20 ₂₀C₁₁

確　率 ₁₀C₈×₁₀C₃ /₂₀C₁₁ = 0.03215



パターン２勝ち負け計場合の数

将　棋 9 1 10 ₁₀C₉

囲　碁 2 8 10 ₁₀C₂

計 11 9 20 ₂₀C₁₁

確　率 ₁₀C₉×₁₀C₂ /₂₀C₁₁ = 0.00268



パターン３勝ち負け計場合の数

将　棋 10 0 10 ₁₀C₁₀

囲　碁 1 9 10 ₁₀C₁

計 11 9 20 ₂₀C₁₁

確　率 ₁₀C₁₀×₁₀C₁ /₂₀C₁₁ = 0.00006

パターン４勝ち負け計場合の数

将　棋 6 4 10 ₁₀C₆

囲　碁 5 5 10 ₁₀C₅

計 11 9 20 ₂₀C₁₁

確　率 ₁₀C₆×₁₀C₅ /₂₀C₁₁ = 0.315075



パターン５勝ち負け計場合の数

将　棋 5 5 10 ₁₀C₅

囲　碁 6 4 10 ₁₀C₆

計 11 9 20 ₂₀C₁₁

確　率 ₁₀C₅×₁₀C₆ /₂₀C₁₁ = 0.315075



パターン６勝ち負け計場合の数

将　棋 4 6 10 ₁₀C₄

囲　碁 7 3 10 ₁₀C₇

計 11 9 20 ₂₀C₁₁

確　率 ₁₀C₄×₁₀C₇ /₂₀C₁₁ = 0.15004

パターン７勝ち負け計場合の数

将　棋 3 7 10 ₁₀C₃

囲　碁 8 2 10 ₁₀C₈

計 11 9 20 ₂₀C₁₁

確　率 ₁₀C₃×₁₀C₈ /₂₀C₁₁ = 0.03215



パターン８勝ち負け計場合の数

将　棋 2 8 10 ₁₀C₂

囲　碁 9 1 10 ₁₀C₉

計 11 9 20 ₂₀C₁₁

確　率 ₁₀C₂×₁₀C₉ /₂₀C₁₁ = 0.00268



パターン９勝ち負け計場合の数

将　棋 1 9 10 ₁₀C₁

囲　碁 10 0 10 ₁₀C₁₀

計 11 9 20 ₂₀C₁₁

確　率 ₁₀C₁×₁₀C₁₀ /₂₀C₁₁ = 0.00006

　この中でデータのような表が得られる確率と同じかそれより小さな確率をすべて加え合わせたものが，有意確率である．すなわち，パターン１，パターン２，パターン３，パターン６，パターン７，パターン８，パターン９，の確率を加え合わせる．　特に，上側確率が，データとパターン１，パターン２，パターン３，を加えたもので，

上側確率：P_upper = 0.15004 + 0.03215 + 0.00268 + 0.00006 = 0.1849

であり，下側確率が残りのパターンの確率を加え，

下側確率：P_lower = 0.15004 + 0.03215 + 0.00268 + 0.00006 = 0.1849

となる．有意確率（p 値）は，これを加え，

p 値：P_upper + P_lower = 0.1849 + 0.1849 = 0.3698

となる．
　ところで，上の表の確率は，白石（将棋） m = 10，黒石（囲碁）n = 10 から勝ち k = 11 を取り出したときの将棋の勝ち数 x の分布で，これは超幾何分布である．これより，有意確率は超幾何分布から出すことができる．

勝率同等性の Fisher 直接確率法検定

# 勝率同等性　Fisher 直接法の R スクリプト
shogi <- c(7, 3) # A の将棋の勝ち負け数　
igo <- c(4, 6) # A の囲碁の勝ち負け数　
x <- rbind(shogi, igo) # 行連結による行列化　
fisher.test(x) # 勝率同等性 Fisher 直接確率　
m <- 10; n <- 10; k <- 11 # 超幾何分布のパラメータ　
phyper(4, m, n, k) # 下側確率　
1- phyper(6, m, n, k) # 上側確率　

**# 勝率同等性　Fisher 直接法の R スクリプト**
shogi <- c(7, 3)	# A の将棋の勝ち負け数
igo <- c(4, 6)	# A の囲碁の勝ち負け数
x <- rbind(shogi, igo)	# 行連結による行列化
fisher.test(x)	# 勝率同等性 Fisher 直接確率
m <- 10; n <- 10; k <- 11	# 超幾何分布のパラメータ
phyper(4, m, n, k)	# 下側確率
1- phyper(6, m, n, k)	# 上側確率

課題：勝敗の比率はそのままで，試行回数を増やして（n = 30）同様な検定を行え．

Fisher の直接確率法の有意水準
　2 × 2 分割表で比率の同等性の検定を行いたいとき，試行数が少ないときは χ² 近似が良くないので，Fisher の直接確率を使うべきだ，とされている．ところで，Fisher の直接確率法（exact test）がどれだけ正確かをシミュレーションで調べてみる．
　成功確率がどちらも p = 0.4 として，試行回数を少なめにして n = 10 の二項分布乱数を２回発生させると 2 × 2 分割表ができ，Fisher の直接確率法で p 値が計算される．いま，帰無仮説の有意水準を 5 ％とすると，p 値が 0.05 以下であれば帰無仮説は棄却される．よって，Fisher の直接確率法の p 値が 5 ％以下になった個数を調べれば，帰無仮説が正しいときの棄却確率（有意水準）がわかる．比較のため，χ² 検定を行ったときの棄却確率も調べる．
　結果をみると，Fisher の直接確率法は帰無仮説の棄却確率が小さく，保守的であると考えられる．理由は不明だが，Fisher の p 値は周辺度数で条件付けたものなので，これが影響しているかも知れない．また，このシミュレーションからみる限り，試行回数が多くないときでも補正なし χ² 検定を用いてもよいような気がする．

# Fisher 直接法の有意水準の R スクリプト
N <- 10000 # シミュレーション回数　
m <- 10 # 試行回数　
y1 <- NULL; y2 <- NULL; y3 <- NULL # 　
for(i in 1:N){ # 　
x <- rbinom(2, m, p=0.4) # n = m，p = 0.4 の二項乱数を２回発生　
xx <- matrix(c(x[1],m-x[1],x[2],m-x[2]), nc=2, byrow=T) # 行列化　
y1 <- c(y1, fisher.test(xx)$p.value) # fisher 直接確率法の p 値を格納　
if(sum(x)==0 || sum(x)==2*m) # 成功回数が両方とも 0 のとき　　
xx <- matrix(c(x[1]+0.5,m-x[1]+0.5,x[2]+0.5,m-x[2]+0.5), nc=2, byrow=T) # セルすべてに 0.5 を加える　　
y2 <- c(y2, chisq.test(xx)$statistic) # 補正つき χ² 値を格納　
y3 <- c(y3, chisq.test(xx, correct=F)$statistic) # 補正なし χ² 値を格納　
} # 　
length(y1[y1<0.05])/N # fisher の p 値が 0.05 未満（有意となった）割合　
q0 <- qchisq(0.95,df=1) # 自由度 1 の χ² 分布 95％点　
length(y2[y2>q0])/N # 補正つき χ² 値の棄却確率　
length(y3[y3>q0])/N # 補正なし χ² 値の棄却確率　

**# Fisher 直接法の有意水準の R スクリプト**
N <- 10000	# シミュレーション回数
m <- 10	# 試行回数
y1 <- NULL; y2 <- NULL; y3 <- NULL	#
for(i in 1:N){	#
x <- rbinom(2, m, p=0.4)	# n = m，p = 0.4 の二項乱数を２回発生
xx <- matrix(c(x[1],m-x[1],x[2],m-x[2]), nc=2, byrow=T)	# 行列化
y1 <- c(y1, fisher.test(xx)$p.value)	# fisher 直接確率法の p 値を格納
if(sum(x)==0 \|\| sum(x)==2*m)	# 成功回数が両方とも 0 のとき
xx <- matrix(c(x[1]+0.5,m-x[1]+0.5,x[2]+0.5,m-x[2]+0.5), nc=2, byrow=T)	# セルすべてに 0.5 を加える
y2 <- c(y2, chisq.test(xx)$statistic)	# 補正つき χ² 値を格納
y3 <- c(y3, chisq.test(xx, correct=F)$statistic)	# 補正なし χ² 値を格納
}	#
length(y1[y1<0.05])/N	# fisher の p 値が 0.05 未満（有意となった）割合
q0 <- qchisq(0.95,df=1)	# 自由度 1 の χ² 分布 95％点
length(y2[y2>q0])/N	# 補正つき χ² 値の棄却確率
length(y3[y3>q0])/N	# 補正なし χ² 値の棄却確率

課題：有意水準 1％の検定を行ったときの棄却確率を求めよ．

クロス集計と独立性の検定

　n 標本を２つの変数 A，B で分類したとき，２つの変数に関連があるかを調べたい．変数 A を集団属性（集団１，集団２），変数 B を反応パターン（反応１，反応２）としたとき，データは以下のようにまとめられる．これをクロス集計と呼ぶ．

2 × 2 分割表データ
　　反応１　　反応２　　計　　

　集団１　 n₁₁ n₁₂ n_1・

　集団２　 n₂₁ n₂₂ n_2・

　計　 n_・1 n_・2 n

**2 × 2 分割表データ**
	反応１	反応２	計
集団１	n₁₁	n₁₂	n_1・
集団２	n₂₁	n₂₂	n_2・
計	n_・1	n_・2	n

　ここで，n_ij は，集団 i の標本の中で，反応 j を取った人数（度数）である．また，n_i・は集団 i の標本の大きさで， n_・j は標本全体（大きさ n）の中で反応 j を取った人数を表し，それぞれ周辺度数という．
　このような表において，集団で反応パターンに違いがなければ，集団 i で反応 j を取る確率は，集団 i である確率 n_i・/n に集団 j である確率 n_・j/n をかけた n_i・n_・j/ n² となることが期待される．これより，集団 i で反応 j を取る人数（度数）は， n_i・n_・j/n となることが期待される．これを独立性の仮定という．
　いま，集団 i の標本の中で，反応 j を取る確率を p_ij とし，集団 i の周辺確率を p_i.，反応 j の周辺確率を p_.j とすると，独立性の仮説は，

帰無仮説，H₀： p_ij ＝ p_i.p_.j，対立仮説，H₁： p_ij ≠ p_i.p_.j，

の検定になる．帰無仮説のもとで，表現は違うが前節とまったく同じ χ² 値が，

と分布するので，独立性の検定を行うことができる．連続性の補正も前節とまったく同じようにして行う．
　すなわち，比率の同等性の検定と独立性の検定は，意味が違うが検定のやり方はまったく同じである．

φ（ファイ）係数

　2 × 2 分割表において，変数 A と変数 B の間の関連の強さを表す指標．四分点相関係数（four-fold point correlation coefficient）とも言う．
　前節の将棋の例でみると，「将棋」という変数と「勝ち」という変数を考える．「将棋」は将棋を行ったとき 1 を取り，「将棋」を行わなかったとき 0 を取る．「勝ち」は勝ったとき 1 を取り，負けたとき 0 を取るものとする．すると，全部で 20 回の対戦結果は，

「将棋」	11111111110000000000
「勝ち」	11111110001111000000

のようにまとめられる．φ 係数は，この 2 つの変数間のピアソン相関係数である．すなわち，「将棋」と「勝ち」の相関である．
　多少の計算により，ピアソン χ² 値との関係は，

であることがわかる．

# φ 係数の R スクリプト

a <- c(rep(1, 10), rep(0, 10)) # 「将棋」の値 b <- c(rep(1, 7), rep(0, 3), rep(1, 4), rep(0, 6)) #「勝ち」の値 cor(a, b) # φ 係数（a，b 間の相関係数） n <- length(a) shogi <- c(7, 3) # A の将棋の勝ち負け数 igo <- c(4, 6) # A の囲碁の勝ち負け数　 x <- rbind(shogi, igo) c2 <- chisq.test(x, correct=F)$statistic # ピアソン χ² 値（連続性補正なし） sqrt(c2/n) # φ 係数

**# φ 係数の R スクリプト**
a <- c(rep(1, 10), rep(0, 10)) # 「将棋」の値 b <- c(rep(1, 7), rep(0, 3), rep(1, 4), rep(0, 6)) #「勝ち」の値 cor(a, b) # φ 係数（a，b 間の相関係数） n <- length(a) shogi <- c(7, 3) # A の将棋の勝ち負け数 igo <- c(4, 6) # A の囲碁の勝ち負け数　 x <- rbind(shogi, igo) c2 <- chisq.test(x, correct=F)$statistic # ピアソン χ² 値（連続性補正なし） sqrt(c2/n) # φ 係数

オッズ比（odds ratio）

　変数 A，B 間の関連の強さを測る指標としてオッズ比がある．たとえば，食中毒事件が起きたとき，食中毒症状が出たか出なかったか（変数 A）を出された食材を食べた人と食べなかった人（変数 B）で分類する．このとき，ある食材に対しての分類は以下のようであったとする．

	発症あり（A₁）	発症なし（A₂）
食べた（B₁）	a	b
食べなかった（B₂）	c	d

　食材を食べたときに発症する確率 Pr[A₁| B₁] の推定値は a/(a + b)，発症しない確率 Pr[A₂| B₁] の推定値は b/(a + b) である．これより，その食材を食べたとき食中毒を発症する危険率（オッズ）は，

Pr[A₁| B₁]/P[A₂| B₁] = a/b

であり，同様に食べなかったときの発症オッズは，

Pr[A₁| B₂]/P[A₂| B₂] = c/d

である．この両者の比，

をオッズ比といい，ある食材を食べたことが食中毒症状発症にどれだけ危険であるかの尺度になる．危険が同等のときは，オッズ比は 1 となる．なお，どこかのセルデータが 0 であったときは，セルのすべての値に 0.5 を加えて補正する．
　ところで，R の fisher.test() では，超幾何分布に基づいてオッズ比の最尤推定を行っているらしいので，上の式の単純な推定値とは値が多少異なっているが，ソースの解読をしていないので詳細は不明である．
　ピアソン χ² 検定は，

帰無仮説　H₀：オッズ比 φ = 1

の検定と同等である．

食中毒原因食材の χ² 独立性検定とオッズ比
　1940 年のNew York 州Oswego の協会の夕食会における胃腸炎異常発生の喫食調査データによる．ケーキと食中毒症状とで以下の関係があった．これより，ケーキが食中毒の原因食材と考えられるか検討できる．

	発症あり	発症なし
食べた	27	13
食べなかった	19	16

# 食材と中毒症状 χ² 検定の R スクリプト
x <- matrix(c(27, 13, 19, 16), nc=2, byrow=T) # ケーキと中毒症状の関係データ　

x[1,1]*x[2,2]/(x[2,1]*x[1,2]) # オッズ比の単純な推定値　

chisq.test(x) # 独立性 χ² 検定　

fisher.test(x) # 独立性 Fisher 直接確率法　

**# 食材と中毒症状 χ² 検定の R スクリプト**
x <- matrix(c(27, 13, 19, 16), nc=2, byrow=T)	# ケーキと中毒症状の関係データ
x[1,1]x[2,2]/(x[2,1]x[1,2])	# オッズ比の単純な推定値
chisq.test(x)	# 独立性 χ² 検定
fisher.test(x)	# 独立性 Fisher 直接確率法

課題：ケーキの他の食材ののデータの一部は以下の表のようであった．このデータから，食中毒の原因食材を推定せよ．

食品名発症あり発症なし

　食べた　食べない　食べた　食べない

ハムステーキ 29 17 17 12

バニラアイス 43 3 11 18

チョコアイス 25 20 22 7

フルーツサラダ 4 42 2 27

食品名	発症あり	発症なし
食べた	食べない	食べた	食べない
ハムステーキ	29	17	17	12
バニラアイス	43	3	11	18
チョコアイス	25	20	22	7
フルーツサラダ	4	42	2	27

シンプソンのパラドックス

　2 元分割表に層構造があるとき，層ごとで解析しないと誤った結論を導くことがある．たとえば，ある政策に対する賛否を 400 名に尋ね，性別，年齢層べつに集計したところ以下のようになった．

賛成反対計

男 132 67 199

女 93 108 201

計 225 175 400

賛成反対計

35 未満 131 67 198

35 以上 94 108 202

計 225 175 400

　これをみると，男性は約 2/3 が賛成してあり，年齢別では 35 未満の賛成も約 2/3 であった．この結果をみると，若い男性がこの政策に賛成していると考えがちである．しかし，性別，年齢別に細かく集計してみると，

賛成反対計

男 35 未満 41 58 99

男 35 以上 91 9 100

計 132 67 199

賛成反対計

女 35 未満 90 9 99

女 35 以上 3 99 102

計 93 108 201

となり，35 歳未満の男性の反対がけっこう多く，予想とは異なる結果となった．このようになった理由は，35 歳以上の男女で賛否がまったく異なっていて，さらに女性でも 35 歳未満と以上で賛否がまったく異なっていたからである．このような状況を無視して，年齢層でひとくくりにしたり，性別でひとくくりしたことが誤った推論を引き起こす原因となったと考えられる．
　このように，まったく異なった性格を持つ集団をまとめてしまってデータの解釈を行うことは危険である．したがって，2 元分割表に基づいて分析をするときは，集団の中に層構造が隠れていないかよく調べる必要がある．

マンテル・ヘンツェル（Mantel-Haenszel）検定

　分割表に層構造があるかを調べる検定

# マンテル・ヘンツェル検定の R スクリプト

Data <- array(c(41, 91, 58, 9, 90, 3, 9, 99), dim = c(2, 2, 2), dimnames = list( 年齢 = c("35 未満", "35 以上"), 賛否 = c("賛成", "反対"), 性別 = c("男性", "女性"))) Data mantelhaen.test(Data)

**# マンテル・ヘンツェル検定の R スクリプト**
Data <- array(c(41, 91, 58, 9, 90, 3, 9, 99), dim = c(2, 2, 2), dimnames = list( 年齢 = c("35 未満", "35 以上"), 賛否 = c("賛成", "反対"), 性別 = c("男性", "女性"))) Data mantelhaen.test(Data)

マクネマー（McNemar）検定

　分割表において，非対角成分である i，j 成分と j，i 成分が等しい（i≠j）を帰無仮説とする検定．この検定は，同一の被験者集団に時期をおいて，首相や政党などへの支持を尋ねたとき，支持が変化したかをみたいときに用いられる．たとえば，ある政策に対する賛否を時期を開けて尋ねたところ，以下の表になったとしよう．

	賛成（2 回目）	反対（2 回目）
賛成（1 回目）	a	b
反対（1 回目）	c	d

1 回目と 2 回目で意見が変わらなかった人数は a と d であり，意見が変わったのが b と c である．帰無仮説は，

H₀：1 回目と 2 回目で賛否の比率が変わらない．

である．帰無仮説のもとでは，反対 → 賛成と賛成 → 反対と変化した人数が等しく (b + c)/2 であることが期待される．すると，ピアソンの χ² 値は，

となるので，これが検定統計量になる．

大統領支持率変化のマクネマー検定
　R のサンプルデータで紹介されている Agresti (1990) のデータによる．選挙権のある年齢のアメリカ人のランダムサンプル 1,600 名の 1 か月での大統領の支持率の変化が以下の表になった．大統領の支持率に変化があったかを調べてみよう．

	支持（2 回目）	不支持（2 回目）
支持（1 回目）	794	150
不支持（1 回目）	86	570

# マクネマー検定の R スクリプト

Performance <- matrix(c(794, 86, 150, 570), nrow = 2, dimnames = list("1 回目調査" = c("支持", "不支持"), "2 回目調査" = c("支持", "不支持"))) Performance mcnemar.test(Performance) # 適切な検定 chisq.test(Performance) # 適切でない検定

**# マクネマー検定の R スクリプト**
Performance <- matrix(c(794, 86, 150, 570), nrow = 2, dimnames = list("1 回目調査" = c("支持", "不支持"), "2 回目調査" = c("支持", "不支持"))) Performance mcnemar.test(Performance) # 適切な検定 chisq.test(Performance) # 適切でない検定

R × C 表

　大きさ n の標本を２つの変数 A，B で分類したとき，２つの変数に関連があるかを調べたい．変数 A が R 個のカテゴリー A₁， A₂，…，A_R，に分かれ，変数 B が C 個のカテゴリー B₁， B₂，…，B_C，に分かれているとすると，標本のうち，カテゴリー A_i，B_j に落ちた個数を n_ij とすると，以下のようび R × C 表にクロス集計される．

R × C 分割表データ
　　B₁　　B₂　　…　　B_C　　計　　

　A₁　 n₁₁ n₁₂ 　…　 n_1C n_1・

　A₂　 n₂₁ n₂₂ 　…　 n_2C n_2・

：：： … ：：

　A_R　 n_R1 n_R2 　…　 n_RC n_R・

　計　 n_・1 n_・2 　…　 n_.C n

**R × C 分割表データ**
	B₁	B₂	…	B_C	計
A₁	n₁₁	n₁₂	…	n_1C	n_1・
A₂	n₂₁	n₂₂	…	n_2C	n_2・
：	：	：	…	：	：
A_R	n_R1	n_R2	…	n_RC	n_R・
計	n_・1	n_・2	…	n_.C	n

すると，2 × 2 分割表のときと同様に，集団 i の標本の中で，反応 j を取る確率を p_ij とし，集団 i の周辺確率を p_i.，反応 j の周辺確率を p_.j とすると，独立性の仮説は，

帰無仮説，H₀： p_ij ＝ p_i.p_.j，対立仮説，H₁： p_ij ≠ p_i.p_.j，

の検定になる．帰無仮説のもとで χ² 値が，

と分布するので，独立性の検定や頻度分布の同等性の検定を行うことができる．

カップヌードルの好みと年代との関連の χ² 検定
　カップヌードルの好みは年代によって違いがあるかどうかを調べた．10 代，20 代，30 代，40 代の被験者をそれぞれ 100 名ずつ選び，好みを聞いたところ以下の表がえられたとしよう（仮想データ）．

帰無仮説 H₀：ヌードルの好みは年代により異ならない

の検定を行ってみる．

年代による好みの違い
　　10 代　　20 代　　30 代　　40 代　計

　カップヌードル　 41 50 　57 　56 　204

　シーフードヌードル　 59 50 　43 　44 　196

　計　 100 100 100 100 400

年代による好みの違い
	10 代	20 代	30 代	40 代	計
カップヌードル	41	50	57	56	204
シーフードヌードル	59	50	43	44	196
計	100	100	100	100	400

グラフに図示すると以下のようになった．若い人（10 代）はシーフードヌードルを好み，比較的年配の人（30 代，40 代）はカップヌードルを好む傾向にありそうに見える．

# カップヌードルの好みの R スクリプト

cup <- c(41, 50, 57, 56) # カップヌードルが好き，年代別データ sea <- c(59, 50, 43, 44) # シーフードヌードルが好き，年代別データ x <- rbind(cup, sea); x chisq.test(x) # χ² 検定

**# カップヌードルの好みの R スクリプト**
cup <- c(41, 50, 57, 56) # カップヌードルが好き，年代別データ sea <- c(59, 50, 43, 44) # シーフードヌードルが好き，年代別データ x <- rbind(cup, sea); x chisq.test(x) # χ² 検定

課題： 30 代と 40 代では，好みに違いがなさそうなので，検定の自由度を減らすため，30 代と 40 代でまとめて， 10 代，20 代，30・40 代の 3 つのカテゴリーにまとめて検定を行なえ．

参考文献（古い順）

Introduction to the Theory of Statistics, Mood, A. M., Graubill, F. A. & Boes, D. C., 1974, McGRAW-HILL
工学のためのデータサイエンス入門－フリーな統計環境Rを用いたデータ解析－，間瀬茂ら，2004，数理工学社
実践生物統計学－分子から生態まで－（第 1 章，第 2 章），東京大学生物測定学研究室編（大森宏ら）， 2004，朝倉書店
The R Tips データ解析環境 R の基本技・グラフィックス活用集，船尾暢男，2005，九天社
R で学ぶデータマインニング I －データ解析の視点から－，熊谷悦生・船尾暢男，2007，九天社
R で学ぶデータマインニング II －シミュレーションの視点から－，熊谷悦生・船尾暢男，2007，九天社

r <- c(7, 4)	# A の将棋の勝数と囲碁の勝数
n <- c(10, 10)	# 将棋の試合回数と囲碁の試合回数
prop.test(r, n, correct=F)	# 比率の同等性検定（連続性の補正なし）
prop.test(r, n)	# 比率の同等性検定（連続性補正）

	成　功	失　敗	計
試行 X	a	b	a + b
試行 Y	c	d	c + d
計	a + c	b + d	N

	成　功	失　敗
試行 X	(a + b)(a + c)/N	(a + b)(b + d)/N
試行 Y	(c + d)(a + c)/N	(c + d)(b + d)/N

x <- matrix(c(7, 3, 4, 6), nc=2, byrow=T)	# A の将棋の勝ち負け数と囲碁の勝ち負け数の行列
shogi <- c(7, 3)	# A の将棋の勝ち負け数
igo <- c(4, 6)	# A の囲碁の勝ち負け数
x <- rbind(shogi, igo)	# 行連結による行列化
chisq.test(x, correct=F)	# 勝率同等性 χ² 検定（連続性の補正なし）
chisq.test(x)	# 勝率同等性 χ² 検定（連続性の補正）

	勝　ち	負　け	計	場合の数
将　棋	7	3	10	₁₀C₇
囲　碁	4	6	10	₁₀C₄
計	11	9	20	₂₀C₁₁

	反応１	反応２	計
集団１	n₁₁	n₁₂	n_1・
集団２	n₂₁	n₂₂	n_2・
計	n_・1	n_・2	n

x <- matrix(c(27, 13, 19, 16), nc=2, byrow=T)	# ケーキと中毒症状の関係データ
x[1,1]x[2,2]/(x[2,1]x[1,2])	# オッズ比の単純な推定値
chisq.test(x)	# 独立性 χ² 検定
fisher.test(x)	# 独立性 Fisher 直接確率法

食品名	発症あり		発症なし
食品名	食べた	食べない	食べた	食べない
ハムステーキ	29	17	17	12
バニラアイス	43	3	11	18
チョコアイス	25	20	22	7
フルーツサラダ	4	42	2	27

	B₁	B₂	…	B_C	計
A₁	n₁₁	n₁₂	…	n_1C	n_1・
A₂	n₂₁	n₂₂	…	n_2C	n_2・
：	：	：	…	：	：
A_R	n_R1	n_R2	…	n_RC	n_R・
計	n_・1	n_・2	…	n_.C	n

	10 代	20 代	30 代	40 代	計
カップヌードル	41	50	57	56	204
シーフードヌードル	59	50	43	44	196
計	100	100	100	100	400

統計特論２

東京大学大学院農学生命科学研究科 大森宏

この講義の目的

０．前期レポート

１．分割表の解析

成功確率（比率）の同等性の近似検定

２×２分割表

Fisher の直接確率法

クロス集計と独立性の検定

φ（ファイ）係数

オッズ比（odds ratio）

シンプソンのパラドックス

マンテル・ヘンツェル（Mantel-Haenszel）検定

マクネマー（McNemar）検定

R × C 表

参考文献（古い順）

東京大学大学院農学生命科学研究科　大森宏