5.正規母集団からの標本に基づく推論
独立な正規分布の合成分布
平均 μ1,分散 σ12,の正規分布からの標本 X ~ N( μ1,σ12 ) と,平均 μ2,分散 σ22,の正規分布からの標本 Y ~ N( μ2,σ22 ) があり,両者が互いに独立であるとする.(Y の値は X の値の影響を受けない.)
-
和の分布
X + Y は平均 μ1 + μ2,分散 σ12 + σ22,の正規分布に従う.
X + Y ~ N( μ1 + μ2, σ12 + σ22 )
-
差の分布
X - Y は平均 μ1 - μ2,分散 σ12 + σ22,の正規分布に従う.
X - Y ~ N( μ1 - μ2, σ12 + σ22 )
-
一般の線形結合の分布
a と b を任意の実数(スカラー)とすると,X と Y の線形結合 aX + bY は,
aX + bY ~ N( aμ1 + bμ2, a2 σ12 + b2 σ22 )
-
標本平均の分布
特に,X1,X2,…,Xn を平均 μ,分散 σ2 の正規分布からの無作為標本であるとすると,標本平均 X- の平均と分散は,それぞれ,
となる.よって,
となり,標本平均 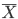 は,平均 μ,分散 σ2/n の正規分布に従う.この分散の平方根
は,平均 μ,分散 σ2/n の正規分布に従う.この分散の平方根 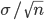 を標本平均
を標本平均 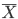 の標準誤差(Standard Error, SE)と呼ぶこともある.
の標準誤差(Standard Error, SE)と呼ぶこともある.
- Thurstone の嗜好モデル
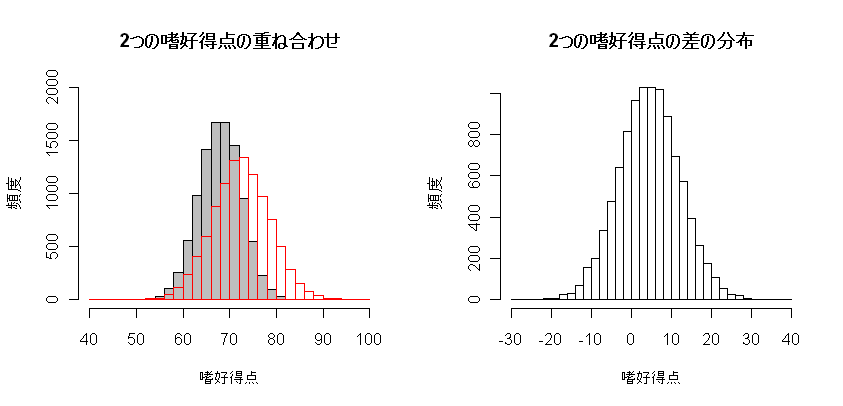
いま、類似した嗜好属性を持つ集団(個人でもよい)を考える.ある商品に対する嗜好は気分などによりぶれるので、
それを正規分布で表現する.ある商品 A に対する嗜好得点が平均 72.5点,標準偏差 6 点の正規分布に従い,商品 B に
対する嗜好得点が平均 68点,標準偏差 4.5点の正規分布に従っていたとする.商品 A と B を棚に並べて販売したときに,
商品 A が売れる確率を考えてみる.
買い物に来たときの商品 A に対する嗜好得点を x,商品 B に対する嗜好得点を y とする.
x が y より大きければ A を買い,x が y より小さければ B を買うと考える.
x ~ N(72.5,36),y ~ N(68,20.25)なので,
u = x - y ~ N(4.5,56.25)に従う.
つまり,
商品 A に対する嗜好得点と商品 B に対する嗜好得点の差は,平均 4.5点,標準偏差 √56.25=7.5点 の
正規分布に従う.この正規分布が 0 より大きくなる確率を求めればよい.
# 2つの商品に対する嗜好得点の差の R スクリプト
|
N <- 10000
| # 標本抽出の回数 |
|
m1 <- 72.5; s1 <- 6
| # 商品 A の平均と標準偏差 |
|
m2 <- 68; s2 <- 4.5
| # 商品 B の平均と標準偏差 |
|
a <- rnorm(N, m1, s1)
| # 商品 A に対する嗜好得点 |
|
b <- rnorm(N, m2, s2)
| # 商品 B に対する嗜好得点 |
|
op <- par(mfrow = c(1, 2))
| # |
|
hist(b, breaks=seq(40,100, by=2), ylim=c(0, 2000), col="gray",ylab="頻度", xlab="嗜好得点", main="")
|
|
title(main="2つの嗜好得点の重ね合わせ")
| # |
|
par(new=T)
| # グラフの重ね合わせ |
|
hist(a, breaks=seq(40,100, by=2), ylim=c(0,2000),density=0.1, ylab="", xlab="",main="", col="red")
|
|
d <- a - b
| # 2つの嗜好得点の差 |
|
hist(d, breaks=seq(-30,40,by=2), ylab="頻度", xlab="嗜好得点",main="")
| # |
|
title(main="2つの嗜好得点の差の分布")
| # |
|
par(op)
| # |
|
length(d[d>0])/length(d)
| # シミュレーションによる確率 |
|
dm <- m1-m2; dv <- s1^2 + s2^2
| # 差の分布の平均と分散 |
|
1 - pnorm(0, mean=dm, sd=sqrt(dv))
| # 差が0以上の確率 |
正規分布に基づく母数の区間推定
正規分布は,平均 μ と分散 σ2 の2つの母数を持つ.2つの母数とも未知であるのが普通であるが,片方が既知であるときは母数に関する推論は簡単に行える.このため,多少非現実的な設定であるが,まず,既知の場合を考え,その後,より一般的である2つの母数とも未知である場合を扱う.
分散既知の場合の母平均 μ の区間推定
正規分布する母集団で母分散 σ
2 がわかっている場合は,未知の母平均 μ に関する区間推定は以下のように行える.
いま,正規分布
N(
μ,σ
2 ) において,大きさ
n の標本
x1,
x2,…,
xn を抽出したとき,母平均は標本平均で推定される.標本平均
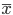
の分布は,
となる.標準正規分布の 97.5%分位点を z0.975(= 1.96)とすると,標準正規分布する確率変数 z が -z0.975 から z0.975 に入る確率は 0.95 となる.つまり,
![{\rm Pr}[-z_{0.975}<\frac{\bar{x}-\mu}{\sigma/\sqrt{n}}<z_{0.975}] = 0.95](images/EXTERN_0007.png)
![{\rm Pr}[\bar{x}-z_{0.975}\cdot \frac{\sigma}{\sqrt{n}}<\mu<\bar{x}+z_{0.975}\cdot \frac{\sigma}{\sqrt{n}}]=0.95](images/EXTERN_0008.png)
![{\rm Pr}[\bar{x}-d<\mu<\bar{x}+d]=0.95, \ d=z_{0.975}\cdot \frac{\sigma}{\sqrt{n}}](images/EXTERN_0009.png)
となる.最後の式を母集団平均 μ の 95% 信頼区間(confidence interval)と言う.
このように,母数の信頼区間を標本から推定することを区間推定という.区間推定においては,信頼区間の幅 2d が小さい程よい.すなわち,母分散が小さい母集団で,標本の大きさ(サンプルサイズ)が大きい程,精度の高い推定が行える.
- 95% の意味
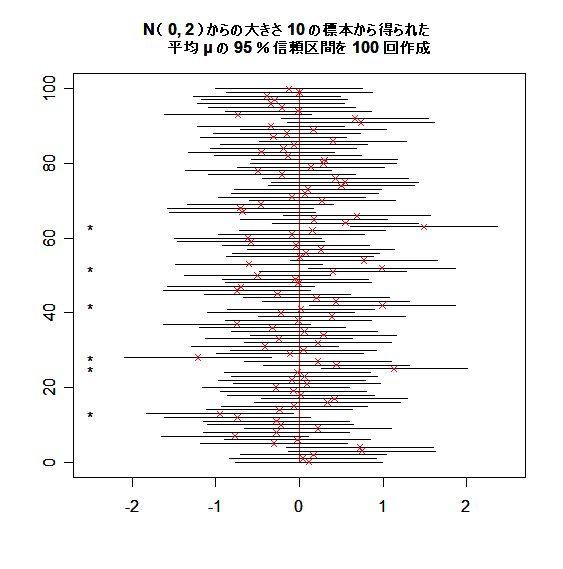
同じ正規母集団から標本抽出を繰り返すと,毎回標本平均として異なる値がえられ,それに
対応して信頼区間も異なる.この信頼区間の 95% が真の平均 μ を含む,という意味である.
つまり,100回の標本抽出により,100 個の信頼区間を作ったら平均的にみて,95 個の信頼区間が
真の平均 μ を含むことが期待できる.
下の図は,平均 0 分散 2 の正規分布 N( 0, 2 ) から大きさ 10 の標本を取りだし,分散が既知であるとして,
母平均に対する信頼区間を 100 個生成したものである."×" が標本平均を示す.左の "*" は,信頼区間
が母平均の真値 0 を含まなかった場合である.
# 平均 μ の 95 %信頼区間 100 回生成の R スクリプト
|
v <- 2; n <- 10
| # 母分散と標本の大きさ |
|
d <- qnorm(0.975)*sqrt(v/n)
| # 95%信頼区間の幅 |
|
x <- c(-2.5, -2.5, 2.5, 2.5)
| # グラフの x の範囲 |
|
y <- c(0, 100, 100, 0)
| # グラフの y の範囲 |
|
plot(x, y, type="n", xlab="", ylab="")
| # グラフ領域確保 |
|
segments(0, 0, 0, 100, col="red")
| # 母平均のライン |
|
for(i in 0:100){
| # 100回の繰り返し |
|
r <- rnorm(n, mean=0, sd=sqrt(v))
| # N(0, v)からの大きさ n の標本平均 |
|
m <- mean(r)
| # 標本平均 |
|
segments(m-d, i, m+d, i)
| # 信頼区間の表示 |
|
points(m, i, pch=4, col="red", cex=0.8)
| # 標本平均の赤×表示 |
|
if(m-d>0 || m+d<0) text(-2.5, i, "*")
| # 信頼区間が母平均を含まない(失敗)した場合 |
|
}
| # |
|
title(main="N( 0, 2 )からの大きさ 10 の標本から得られた
| |
|
平均 μ の 95 %信頼区間を 100 回作成", cex.main=1.0)
| # |
平均既知の場合の母分散 σ2 の区間推定
正規母集団で母平均 μ がわかっているとき,大きさ n の標本 x1,x2,…,xn を抽出したとき,母分散は,
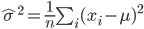
で推定される.ところで,標本は
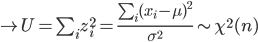
と分布するので,自由度 n の χ2 の 2.5%分位点と 97.5%分位点をそれぞれ, χ2(n)0.025,χ2(n)0.975 とすると,
![{\rm Pr}\bigl[ \chi^2(n)_{0.025}<\frac{\sum(x_i-\mu)^2}{\sigma^2}<\chi^2(n)_{0.975}\bigr]=0.95](images/EXTERN_0013.png)
![{\rm Pr} \Bigl[ \frac{\sum(x_i-\mu)^2}{\chi^2(n)_{0.975}} <\sigma^2 < \frac{\sum(x_i-\mu)^2}{\chi^2(n)_{0.025}} \Bigr]=0.95](images/EXTERN_0014.png)
が成り立つ.下の式の区間を母分散 σ2 の 95%信頼区間と言う.
平均未知の場合の母分散 σ2 の区間推定
正規母集団では,母数が未知であるのが普通であろう.このとき,大きさ
n の標本
x1,
x2,…,
xn を抽出したとき,母平均
μ と母分散 σ
2 は,そえぞれ標本平均
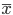
と標本分散
s2,
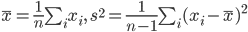
で推定される.母平均 μ の信頼区間を述べる前に母分散 σ2 の信頼区間の構成法を述べる.
ところで,標本や標本平均は,
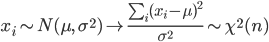
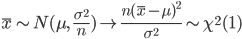
と分布する.一方,
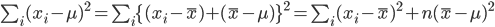
と計算されるので,(n - 1)s2/σ2 という量は,
と,自由度 n - 1 の χ2 分布に従うことがわかる.
自由度 n - 1 の χ2 分布の 2.5%分位点と 97.5%分位点をそれぞれ, χ2(n - 1)0.025,χ2(n - 1)0.975 とすると,
が成り立つ.下の式の区間を母分散 σ2 の 95%信頼区間と言う.
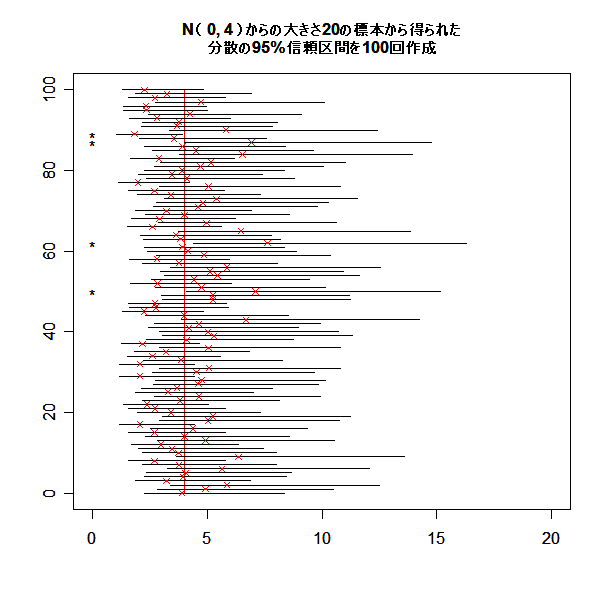
- 母分散 σ2 の 95%信頼区間
母平均が未知のときの母分散 σ2 の 95%信頼区間を,
母平均に対する信頼区間と同様に100回作ってみる.
# 母分散 σ2
の 95 %信頼区間 100 回生成の R スクリプト
|
m <- 20; v <- 4
| # 正規母集団の平均と分散 |
|
n <- 20
| # 標本の大きさ |
|
x <- c(0, 0, 20, 20)
| # グラフの x の範囲 |
|
y <- c(0, 100, 100, 0)
| # グラフの y の範囲 |
|
plot(x, y, type="n", xlab="", ylab="")
| # グラフ領域確保 |
|
segments(v, 0, v, 100, col="red")
| # 母分散のライン |
|
for(i in 0:100){
| # 100回の繰り返し |
|
r <- rnorm(n, m, sqrt(v))
| # 母集団からの無作為標本 |
|
s <- (n-1)*var(r)
| # 標本の偏差平方和 |
|
s1 <- s/qchisq(0.975, df=n-1)
| # 95 %信頼区間の下限 |
|
s2 <- s/qchisq(0.025, df=n-1)
| # 95 %信頼区間の上限 |
|
segments(s1, i, s2, i)
| # 信頼区間の表示 |
|
points(var(r), i, pch=4, col="red", cex=0.8)
| # 標本分散の赤×表示 |
|
if(s1 > v || s2 < v) text(0, i, "*")
| # 信頼区間が母分散を含まない(失敗)した場合 |
|
}
| # |
|
title(main="N( 20, 4 )からの大きさ20の標本から得られた
|
|
分散の95%信頼区間を100回作成", cex.main=1.0)
| # |
分散未知の場合の母平均 μ の区間推定
前節で考えたように,正規母集団の母数が未知ときは,大きさ
n の標本
x1,
x2,…,
xn から,母平均
μ と母分散 σ
2 は,そえぞれ標本平均
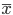
と標本分散
s2 で推定される.
標本平均
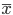
の分布は標準化すると,
のように標準正規分布となり,標本分散に関係する量は,
のように自由度 n - 1 の χ2 分布する.これより,z と U をその自由度 n - 1 で割った量の平方根との比は,
のように自由度 n - 1 の t 分布に従う.
自由度 n - 1 の t 分布の 97.5%分位点を t(n - 1)0.975 とすると, t 分布する確率変数 t 値が -t(n - 1)0.975 から t(n - 1)0.975 に入る確率は 0.95 となる.つまり,
となる.最後の式を母分散未知のときの母集団平均 μ の 95% 信頼区間と言う.
- 課題:
母分散既知のときの母集団平均 μ の 95% 信頼区間100回生成の R スクリプトを参考にして,
母分散未知のときの母集団平均 μ の 95% 信頼区間を100回生成し,母分散が未知と既知で
信頼区間にどのような違いがあるか考えよ.
6.確率変数の関数の分布
6-1.確率変数の和の分布
確率変数 X1,…,Xn に対し,
![{\rm E} \bigl[ \sum_i X_i \bigr] = \sum_i {\rm E}[X_i]](images/EXTERN_0028.png)
,
![{\rm Var} \bigl[ \sum_i X_i \bigr] =\sum_i {\rm Var}[X_i] + 2\sum \sum_{i<j} {\rm cov} [X_i, X_j]](images/EXTERN_0029.png)
が成り立つ.
5-2.変数変換
X を密度関数 fX(x) をもつ連続型確率変数としたとき,y = g(x) が 1 対 1 の変換であり,x = g-1(y) の導関数が連続で 0 にならないとすると,Y の確率密度関数は,
となる.
5-3.デルタ(Delta method)法
確率変数
X の平均と分散が
![\mu_X ={\rm E}[X], \ \sigma^2_X = {\rm Var}[X],](images/EXTERN_0035.png)
であるとする.このとき,
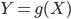
,という変数変換を行ったとする.デルタ法とは
g(
X) を
X の平均のまわりでテイラー展開することにより,
Y の平均や分散を
X の平均や分散で近似的に表す方法である.1 次の項までのテイラー展開は,
なので,これの分散をとると,
となる.このように Y の分散は X の平均と分散の値から近似的に求めることができる.
平均に関しては 2 次の項までテイラー展開し,
これの期待値をとり,
として近似の精度をより上げることができる.
5-4.積の分布
確率変数 X,Y の平均が μX,μY であるとき,
![{\rm E}[XY]=\mu_X \mu_Y + {\rm cov}[X,Y]](images/EXTERN_0041.png)
![{\rm Var}[XY]=\mu_Y^2 {\rm Var}[X] + \mu_X^2 {\rm Var}[Y] + 2\mu_X \mu_Y {\rm cov}[X,Y]-({\rm cov}[X,Y])^2](images/EXTERN_0042.png)
![+{\rm E}[(X-\mu_X)^2 (Y-\mu_Y)^2 ]+2\mu_Y {\rm E}[(X-\mu_X)^2 (Y-\mu_Y)]+2\mu_Y {\rm E}[(X-\mu_X)(Y-\mu_Y)^2]](images/EXTERN_0043.png)
が成り立つ.
5-5.比の分布
確率変数 X,Y の平均が μX,μY であるとき,2 変数関数のデルタ法(省略)を用いると,
![{\rm E} \Bigl[ \frac{X}{Y} \Bigr] \approx \frac{\mu_X}{\mu_Y} - \frac{1}{\mu_Y^2} {\rm cov}[X, Y] + \frac{\mu_X}{\mu_Y^3} {\rm Var}[Y]](images/EXTERN_0044.png)
![{\rm Var} \Bigl[ \frac{X}{Y} \Bigr] \approx \Bigl( \frac{\mu_X}{\mu_Y} \Bigr)^2 \Bigl( \frac{ {\rm Var}[X]}{\mu_X^2} + \frac{ {\rm Var}[Y]}{\mu_Y^2} - \frac{2{\rm cov}[X,Y]}{\mu_X \mu_Y} \Bigr)](images/EXTERN_0045.png)
の近似が成り立つ.
5-6.最大値,最小値の分布
n 個の互いに独立で同一の分布をもつ確率変数 X1,…,Xn に対し,Y1 = min(X1,…,Xn),Yn = max(X1,…,Xn),とする.最大値 Yn の累積分布関数と確率密度関数はそれぞれ,
![F_{Y_n}(y) = {\rm Pr}[Y_n \leq y]={\rm Pr}[X_1 \leq y, \ \cdots \ , X_n \leq y]](images/EXTERN_0046.png)
![=\prod_i {\rm Pr}[X_i \leq y] =\prod_i F_{X_i}(y)=[F_X(y)]^n](images/EXTERN_0047.png)
![f_{Y_n} (y) =\frac{d}{dy} F_{Y_n}(y) = n[F_X(y)]^{n-1}f_X(y)](images/EXTERN_0048.png)
となる.また,最小値 Y1 の分布は,
![F_{Y_1}(y) = {\rm Pr}[Y_1 \leq y] =1-{\rm Pr}[Y_1 >y ] = 1- {\rm Pr}[X_1>y, \ \cdots \ , X_n>y]](images/EXTERN_0049.png)
![=1-\prod_i {\rm Pr}[X_i>y]=1- \prod_i[1 - F_{X_i}(y)]=1-[1-F_X(y)]^n](images/EXTERN_0050.png)
![f_{Y_1}(y) = \frac{d}{dy} F_{Y_1}(y) = n[1-F_X(y)]^{n-1}f_X(y)](images/EXTERN_0051.png)
となる.
-
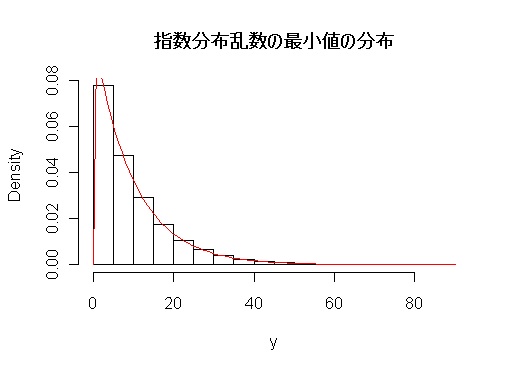
指数分布の最小値の分布
ある電球の寿命が平均 100 日の指数分布に従っているとする.このような電球を 10 個同時につけたとすると,最初に切れる電球の寿命分布とその平均はどうなるか.
個々の電球 Xi の確率密度関数と累積分布関数はパラメータ λ = 1/100 の指数分布なので,
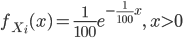
![F_{X_i}(x) = \int_0^x f_{X_i}(t)dt = \int_0^x \frac{1}{100}e^{-\frac{1}{100}t} dt=\Bigl[-e^{-\frac{1}{100}t}\Bigr]_0^x=1-e^{-\frac{1}{100}x}](images/EXTERN_0053.png)
である.最初に切れる電球の寿命分布は最小値の分布,Y1 = min(X1,…,X10),であるので,
![f_{Y_1}(y)=10 \Bigl[1- \bigl(1-e^{-\frac{1}{100}y} \bigr) \Bigr]^{10-1} \Bigl(\frac{1}{100} e^{-\frac{1}{100}y } \Bigr)=\frac{10}{100}e^{-\frac{10}{100}y}=\frac{1}{10}e^{-\frac{1}{10}y}](images/EXTERN_0054.png)
となる.これは, パラメータ λ = 1/10 の指数分布なので,その平均は 10 である.
# 指数分布の最小値分布の R スクリプト
N <- 10000
n <- 10
x <- matrix(rexp(n*N, 1/100), ncol=n)
y <- apply(x, 1,min)
hist(y,freq=F, main="")
curve(dexp(x, 1/10), add=T, col=2)
title(main="指数分布乱数の最小値の分布")
|
- 課題:正規分布の最大値の分布はどうなるか.
![{\rm E}[\bar{X}]={\rm E}[\frac{1}{n}\sum_iX_i]=\frac{1}{n}{\rm E}[X_i]=\frac{1}{n}n\mu=\mu](images/EXTERN_0000.png)
![{\rm Var}[\bar{X}]={\rm Var}[\frac{1}{n}\sum_i X_i]=\frac{1}{n^2}\sum_i{\rm Var}[X_i]=\frac{1}{n^2}n\sigma^2=\frac{\sigma^2}{n}](images/EXTERN_0001.png)
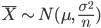
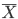 は,平均 μ,分散 σ2/n の正規分布に従う.この分散の平方根
は,平均 μ,分散 σ2/n の正規分布に従う.この分散の平方根 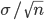 を標本平均
を標本平均 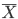 の標準誤差(Standard Error, SE)と呼ぶこともある.
の標準誤差(Standard Error, SE)と呼ぶこともある.
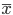 の分布は,
の分布は,
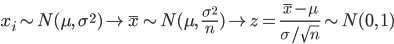
![{\rm Pr}[-z_{0.975}<\frac{\bar{x}-\mu}{\sigma/\sqrt{n}}<z_{0.975}] = 0.95](images/EXTERN_0007.png)
![{\rm Pr}[\bar{x}-z_{0.975}\cdot \frac{\sigma}{\sqrt{n}}<\mu<\bar{x}+z_{0.975}\cdot \frac{\sigma}{\sqrt{n}}]=0.95](images/EXTERN_0008.png)
![{\rm Pr}[\bar{x}-d<\mu<\bar{x}+d]=0.95, \ d=z_{0.975}\cdot \frac{\sigma}{\sqrt{n}}](images/EXTERN_0009.png)
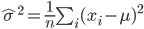
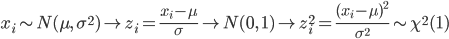
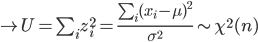
![{\rm Pr}\bigl[ \chi^2(n)_{0.025}<\frac{\sum(x_i-\mu)^2}{\sigma^2}<\chi^2(n)_{0.975}\bigr]=0.95](images/EXTERN_0013.png)
![{\rm Pr} \Bigl[ \frac{\sum(x_i-\mu)^2}{\chi^2(n)_{0.975}} <\sigma^2 < \frac{\sum(x_i-\mu)^2}{\chi^2(n)_{0.025}} \Bigr]=0.95](images/EXTERN_0014.png)
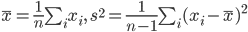
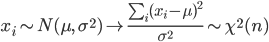
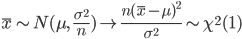
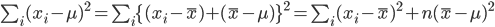
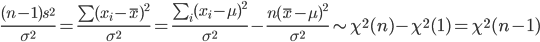
![{\rm Pr}\bigl[ \chi^2(n-1)_{0.025}<\frac{(n-1)s^2}{\sigma^2}<\chi^2(n-1)_{0.975}\bigr]=0.95](images/EXTERN_0020.png)
![{\rm Pr} \Bigl[ \frac{\sum(x_i-\mu)^2}{\chi^2(n-1)_{0.975}} <\sigma^2 < \frac{\sum(x_i-\mu)^2}{\chi^2(n-1)_{0.025}} \Bigr]=0.95](images/EXTERN_0021.png)
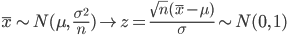
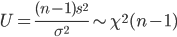
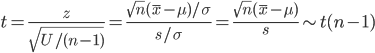
![{\rm Pr}[-t(n-1)_{0.975}<\frac{\sqrt{n}(\bar{x}-\mu)}{\sigma}<t(n-1)_{0.975}] = 0.95](images/EXTERN_0025.png)
![{\rm Pr}[\bar{x}-t(n-1)_{0.975}\cdot \frac{s}{\sqrt{n}}<\mu<\bar{x}+t(n-1)_{0.975}\cdot \frac{s}{\sqrt{n}}]=0.95](images/EXTERN_0026.png)
![{\rm Pr}[\bar{x}-d<\mu<\bar{x}+d]=0.95, \ d=t(n-1)_{0.975}\cdot \frac{s}{\sqrt{n}}](images/EXTERN_0027.png)
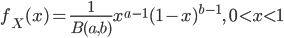
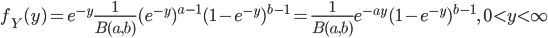
![B(a,1)=\int_0^1x^{a-1}dx =\frac{1}{a}[x^a]_0^1=\frac{1}{a}](images/EXTERN_0033.png)
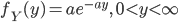
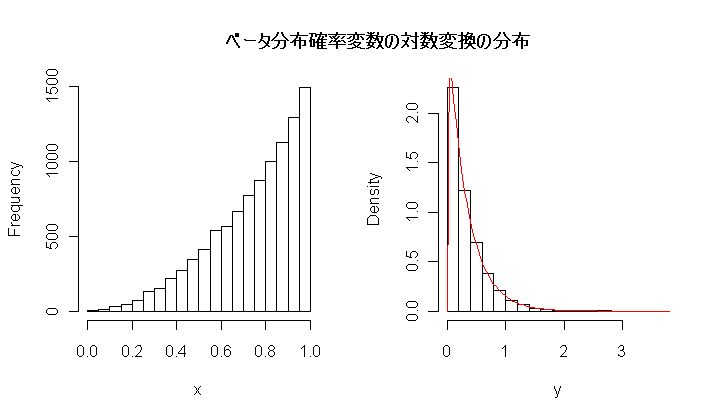
![\mu_X ={\rm E}[X], \ \sigma^2_X = {\rm Var}[X],](images/EXTERN_0035.png) であるとする.このとき,
であるとする.このとき,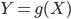 ,という変数変換を行ったとする.デルタ法とは g(X) を X の平均のまわりでテイラー展開することにより, Y の平均や分散を X の平均や分散で近似的に表す方法である.1 次の項までのテイラー展開は,
,という変数変換を行ったとする.デルタ法とは g(X) を X の平均のまわりでテイラー展開することにより, Y の平均や分散を X の平均や分散で近似的に表す方法である.1 次の項までのテイラー展開は,
![F_{Y_1}(y) = {\rm Pr}[Y_1 \leq y] =1-{\rm Pr}[Y_1 >y ] = 1- {\rm Pr}[X_1>y, \ \cdots \ , X_n>y]](images/EXTERN_0049.png)
![=1-\prod_i {\rm Pr}[X_i>y]=1- \prod_i[1 - F_{X_i}(y)]=1-[1-F_X(y)]^n](images/EXTERN_0050.png)
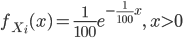
![F_{X_i}(x) = \int_0^x f_{X_i}(t)dt = \int_0^x \frac{1}{100}e^{-\frac{1}{100}t} dt=\Bigl[-e^{-\frac{1}{100}t}\Bigr]_0^x=1-e^{-\frac{1}{100}x}](images/EXTERN_0053.png)
![f_{Y_1}(y)=10 \Bigl[1- \bigl(1-e^{-\frac{1}{100}y} \bigr) \Bigr]^{10-1} \Bigl(\frac{1}{100} e^{-\frac{1}{100}y } \Bigr)=\frac{10}{100}e^{-\frac{10}{100}y}=\frac{1}{10}e^{-\frac{1}{10}y}](images/EXTERN_0054.png)