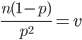7.分布パラメータの推定
7-1.尤度(likelihood)
パラメータの関数としての尤度
パラメータ θ をもった分布 f(x;θ) からの無作為標本(random sample) X1,…,Xn が得られたとする.このとき,標本の同時分布の確率密度は,
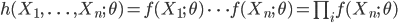
と表せる.これを,標本が与えられたときのパラメータ θ の関数とみなし,
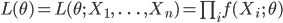
と表記する.これを,標本 X1,…,Xn の尤度(関数)という.尤度は確率モデル f(x;θ) のもとで,標本 X1,…,Xn が得られる確率に比例した量である.
対数尤度(log likelihood)
尤度は積の形で少し扱いにくいので,尤度の対数を取り和の形にした対数尤度
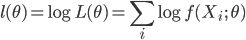
を用いることも多い.
なお,対数尤度を
θ で微分でした関数をスコア関数 (score function)
S(
θ) と呼ぶこともある.すなわち,
である.
Fisher 情報量 (Fisher Information)
対数尤度の 2 階偏導関数は

の近傍で負となる(
L(
θ) が上に凸)となるので,この関数を
と定義したとき,これの期待値,
を Fisher 情報量 (expected Fisher Information) と言う.また,最尤推定量

のもとでのこの関数の値
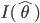
を Fisher 情報量 (observed Fisher Information) ということもある.一般に,
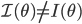
であるが,正規分布やポアソン分布などの指数分布族では
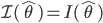
である.
一般に,
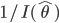
が

の分散の近似推定値になる.すなわち,
である.なお,se(

) は

の標準誤差 (standrad error) である.
以下,正規分布の場合
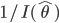
が

の分散に一致することを示す.
7-2.統計的推定
母集団(population)分布の形がパラメータ(母数)θ をもった f(x;θ) であると想定できる場合,母集団から大きさ n の無作為標本(random sample), X1,…,Xn,を抽出し,その標本から母集団分布のパラメータ θ を推定する.たとえば,母集団が正規分布すると想定される場合,母集団母数は平均 μ,分散 σ2 になる.すなわち, θ = (μ,σ2)である.
統計量(statistic)
母集団からの無作為標本の任意の関数で未知のパラメータを含まないものを統計量という.これは,
T = t(X1,…,Xn)
と表される.たとえば,標本平均,最大値,などである.標本の実現値であるデータや観測値(observation)が与えられると,統計量の具体的な値が定まる.
点推定(point estimation)
分布パラメータ θ の値そのもの,もしくは,その関数 τ(θ) の値を推定することである. θ を推定した量を  と表記し,これを推定量(estimator)と呼ぶ.推定量は確率変数の関数(推定関数)で,統計量で構成される.標本の観測値が得られたときの推定量の実現値を推定値(estimate)と呼んで区別することもある.
と表記し,これを推定量(estimator)と呼ぶ.推定量は確率変数の関数(推定関数)で,統計量で構成される.標本の観測値が得られたときの推定量の実現値を推定値(estimate)と呼んで区別することもある.
区間推定(interval estimation)
分布パラメータ θ が含まれる範囲を確率的に
のように推定すること.
推定量には何でもなれる
分布の未知パラメータ(母数) θ の推定量としてはどのようなものもなりうる.極端な例では,どのような標本が得られたかにかかわらず,母集団平均は 1 である,という推定方式や,最初に得られた標本の値を母集団平均とする,という方式も考えられる.このような推定方式では,母集団に対して有益な情報を与えることはほとんどないが,たまたま母集団パラメータを正確に推定することもある.つまり,競馬の単勝馬券(1 着となる馬番号を当てる)で何も考えずに 3 番の馬券を買い続ければ,たまには的中することもあるのと同じである.
このため,推定量の良さを測る尺度が必要になる.
一致推定量(consistent estimator)
母集団から大きさ
n の標本
X1,…,
Xn を抽出して分布パラメータ
θ の推定量
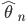
を構成したとする.このとき,標本の大きさ
n を大きくしていけば母集団母数
θ を正しく推定できることが必要であろう.つまり,任意の
ε > 0 に対して,
が成り立つ.これは,データをたくさん集めればそれだけ母集団に対して正しい知識を与える推定方法を行っていることを保証するものである.
大数の法則により,標本平均
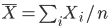
は母集団平均の一致推定量であることがわかる.
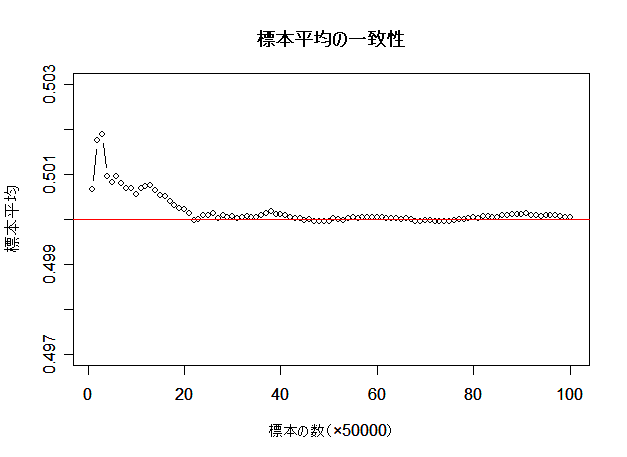
- 一様分布の標本平均の一致性
(0,1)一様分布から毎回 n = 500 の標本を抽出して追加し,標本平均を求める.回数を重ねるごとに
標本の大きさが n だけ増えていくので,標本平均が母集団平均 μ = 0.5 に近づく様子が観察されるはずである.
# 標本平均の一致性の R スクリプト
|
N <- 100
| # シミュレーション回数 |
|
n <- 50000
| # 1回のサンプルサイズ |
|
s <- 0
| # 乱数の和 |
|
q <- numeric(0)
| # 毎回の標本平均 |
|
for(i in 1:N){
| # |
|
s <- s + sum(runif(n))
| # 乱数の和をたす |
|
q <- c(q, s/(n*i))
| # 今回までの標本平均 |
|
}
| # |
|
plot(q, type="b", xlab="標本の数(×50000)", ylab="標本平均", ylim=c(0.497,0.503))
|
|
abline(h=0.5, col=2)
| # 真値のライン |
|
title(main="標本平均の一致性")
| # |
平均2乗誤差(Mean Squared Error : MSE)
推定量の良さを測る最も一般的な尺度である.分布パラメータ θ を統計量 T で推定したとき,平均 2 乗誤差は,T と θ との偏差の 2 乗の期待値で表される.すなわち,
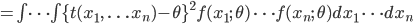
と定義される.MSE は θ の関数であるが,どのような θ に対しても MSE が小さいような推定量 T があればよいが一般には存在しない.
一方,MSE は,
![{\rm MSE}(\theta) = {\rm E}[(T-\theta)^2 ] = {\rm E}[ \{(T-{\rm E}[T])-({\rm E}[T]-\theta) \}^2 ]](images/EXTERN_0028.png)
![={\rm E}[(T-{\rm E}[T])^2] + {\rm E}[ ({\rm E}[T]-\theta)^2 ]={\rm Var}[T]+(\theta-{\rm E}[T])^2](images/EXTERN_0029.png)
と変形される.ここで,θ - E[T] は推定量 T の偏り(バイアス(bias))と呼ばれる量である.つまり,平均 2 乗誤差は,推定量の分散とバイアスの 2 乗の大きさに分解できる.
なお,推定量 T の分散 Var[T] の平方根を標準誤差(Standard Error : SE)と呼ぶ.
不偏推定量(unbiased estimator)
分布パラメータ θ の推定量 T の中で,
となるものを不偏推定量という.
-
標本平均の不偏性
平均 μ,分散 σ2 である母集団(正規分布でなくてもよい)から大きさ n の無作為標本 X1,…,Xn を抽出した.
標本平均は不偏推定量である.なぜなら,
だからである.一方,標本平均の分散は,
となり,標本平均の分散は標本の大きさ(サンプルサイズ)に反比例して,サンプルサイズが大きくなるほど母集団平均のまわりに集中して分布する.
-
標本分散の不偏性
平均 μ,分散 σ2 である母集団から大きさ n の無作為標本 X1,…,Xn を抽出した.標本平均を 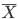 としたとき,
としたとき,
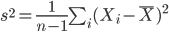
を標本(不偏)分散という.標本分散は,
![{\rm E}[s^2] = {\rm E} \Bigl[ \frac{1}{n-1} \sum_i(X_i-\bar{X})^2 \Bigr]=\frac{1}{n-1} {\rm E}[
\sum(X_i-\mu)^2-n(\bar{X}-\mu)^2]](images/EXTERN_0035.png)
![=\frac{1}{n-1} \bigl{ \sum {\rm E}[(X_i-\mu)^2]-n{\rm E}[(\bar{X}-\mu)^2] \bigr} = \frac{1}{n-1} \bigl{\sum {\rm Var}[X_i]-n{\rm Var}[\bar{X}] \bigr}](images/EXTERN_0036.png)
であるので,母集団分散 σ2 の不偏推定量であることがわかる.一方,サンプルサイズ n で割る分散推定量
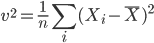
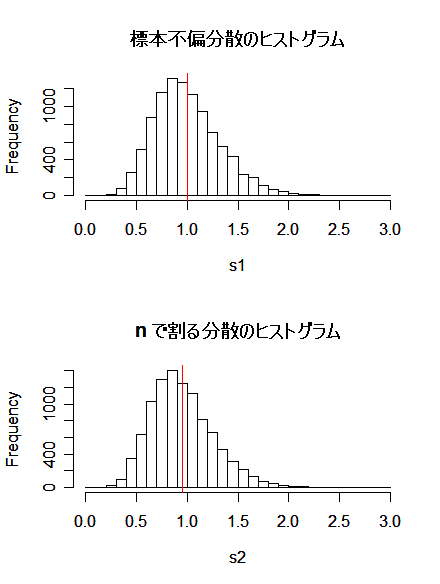
は不偏ではない.これをシミュレーションで確認してみよう,
すなわち,標準正規分布から大きさ n = 20 の標本を取り出して,標本分散 s2 と分散推定量 v2 をそれぞれ N = 10000 個生成し,それらの平均値を計算することで不偏かどうかがわかる.標本分散 s2 の平均は 1.00 で不偏であったが, n で割る分散推定量 v2 の平均は 0.95 で分散推定が小さい方へのバイアスがあることがわかった.
# 標本分散の不偏性の R スクリプト
|
N <- 10000
| # シミュレーション回数 |
|
n <- 20
| # サンプルサイズ |
|
s1 <- NULL
| # |
|
s2 <- NULL
| # |
|
for(i in 1:N){
| # |
|
x <- rnorm(n)
| # 標準正規乱数 n 個 |
|
s <- var(x)
| # 標本分散 |
|
s1 <- c(s1, s)
| # 標本分散列 |
|
s2 <- c(s2, s*(n-1)/n)
| # n で割る分散列 |
|
}
| # |
|
m1 <- mean(s1)
| # 標本分散の平均 |
|
m2 <- mean(s2)
| # n で割る分散の平均 |
|
op <- par(mfrow = c(2, 1))
| # |
|
hist(s1, breaks=seq(0,3, by=0.1), main="")
| |
abline(v = m1, col=2)
| # 平均の赤線表示 |
|
title(main="標本不偏分散のヒストグラム")
|
|
hist(s2, breaks=seq(0,3, by=0.1), main="")
| |
abline(v = m2, col=2)
| # 平均の赤線表示 |
|
title(main="n で割る分散のヒストグラム")
|
|
par(op)
| # |
|
m1
| # 標本分散の平均 |
|
m2
| # n で割る分散の平均 |
|
 |
不偏推定量のクラスの中では,平均 2 乗誤差は推定量の分散 Var[T] と等しくなるので,分散最小の推定量が望ましいことになる.
Cramer - Rao の下限(Cramer - Rao lower bound)
不偏推定量のクラスで到達可能な分散の下限は,Cramer - Rao により与えられている.
いま,分布パラメータ θ のある関数 τ(θ) の不偏推定量 T の分散の下限は, Fisher 情報量を用いて,
![{\rm Var}[T] \geq \frac{[\tau'(\theta)]^2}{ \calI (\theta)}](images/EXTERN_0039.png)
となることが知られている.Cramer - Rao の下限に一致する分散をもつ不偏推定量を有効(efficient)と言う.
-
分散既知の正規分布母集団に対する標本平均の有効性
分散が σ
02 と既知の正規母集団 N(μ,σ
02) から大きさ
n の無作為標本
x1,…,
xn を抽出した.標本平均
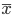
の分布は,
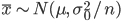
であり,もちろん,
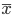
は不偏である.分散既知の正規分布では,大きさ n の無作為標本の Fisher 情報量は,前節の結果より,
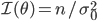
であり,
τ'(
θ) =
μ' = 1,に注意すると, Cramer - Rao の分散の下限は,
となる.これは,標本平均
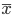
の分散に一致する.よって,標本平均は分散既知の正規母集団の平均に対する有効な推定量,すなわち,最良であることがわかる.
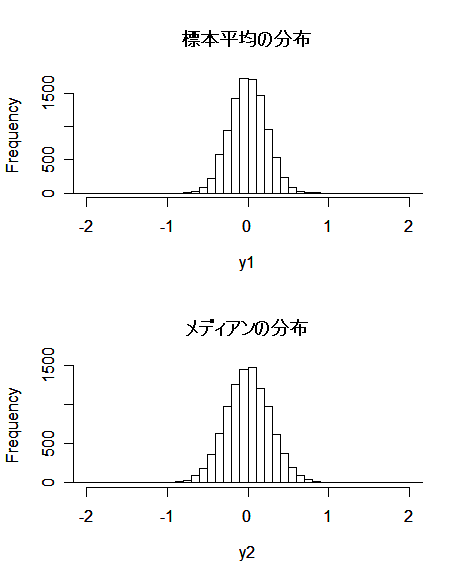
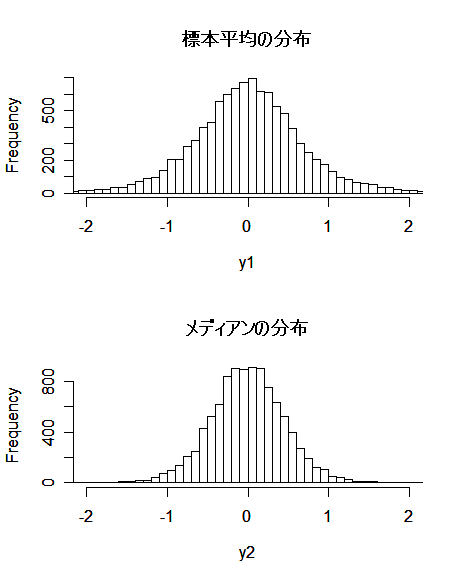
- 分散既知の正規母集団に対するメディアンの分散
分散が σ02 と既知の正規母集団 N(μ,σ02) から
大きさ n の無作為標本 X1,…,Xn を抽出した.
メディアン(中央値) M は漸近的(標本の大きさ n が大きくなるにつれて)に
M ~ N(μ,πσ02/(2n))
の正規分布に従うことが知られている.すなわち,メディアン M は,標本平均の分散
より π/2 ≒ 1.57 倍分散が大きい.推定量の標準偏差である標準誤差(SE)でいうと,
メディアンの標準誤差は標本平均の標準誤差の √π/2 ≒ 1.25 倍である.
このため,標本平均と同程度の標準誤差(精度)を得るには 1.57倍の標本が
必要になる.この値の逆数 2/π ≒ 0.637 を相対漸近効率と言う.正規母集団における
メディアンの(Cramer - Rao の下限に対する)有効性は 63.7%であるといえる.
# メディアンの分散の R スクリプト
|
N <- 10000
| # シミュレーション回数 |
|
n <- 20
| # サンプルサイズ |
|
y1 <- NULL
| # |
|
y2 <- NULL
| # |
|
for(i in 1:N){
| # |
|
x <- rnorm(n)
| # 標準正規乱数 n 個 |
|
y1 <- c(y1, mean(x))
| # 標本平均列 |
|
y2 <- c(y2, median(x))
| # メディアン列 |
|
}
| # |
|
m1 <- mean(y1); m2 <- mean(y2)
| # 標本平均とメディアンの平均 |
|
s1 <- var(y1); s2 <- var(y2)
| # 標本平均とメディアンの分散 |
|
s2/s1
| # 分散比 |
|
sqrt(s1) | # 標本平均の標準誤差 |
|
sqrt(s2) | # メディアンの標準誤差 |
|
op <- par(mfrow = c(2, 1))
| # |
|
hist(y1, breaks=seq(-4,4, by=0.1), xlim=c(-2, 2), main="")
|
|
title(main="標本平均の分布")
| # |
|
hist(y2, breaks=seq(-4,4, by=0.1), xlim=c(-2, 2), main="")
|
|
title(main="メディアンの分布")
| # |
|
par(op)
| # |
|
 |
頑健(ロバスト)性(robustness)
データ(標本の実現値)が正規分布から由来するのであれば,母平均の推定量として標本平均が最小分散をもつ
不偏推定量なので,最良である.しかしながら,実際のデータが正規分布から由来するとは限らない場合もある.
このようなときや外れ値(outlier)があるときでもそれなりの推定が行える推定量をロバストである,という.
メディアンは,標本平均よりロバストであることが知られている.
いま,正規分布より裾の重い t 分布を考えてみる.母集団分布が t 分布であるときの標本平均とメディアンの
分布を比較すればロバスト性が評価できる.自由度 2 の t 分布では極端な値が出やすいので,標本平均の
分散はとても大きくなっている.
8.最尤法
分布パラメータの推定法として,最もよく用いられるのが最尤法である.
最尤推定量(Maximum Likelihood Estimator : MLE)
標本の尤度は,標本が生成する確率モデル f(x;θ) のもとでの標本の同時確率密度なので,想定した確率モデル f(x;θ) のもとで標本が生起する(データのような標本が実現する)確率に比例した量になる.この標本の "生起確率" を最大にするような分布パラメータ θ を求めることを最尤法という.最尤法により得られたパラメータの推定量を最尤推定量という.
多くの場合,最尤推定量は尤度をパラメータ θ で微分して 0 とおいた,
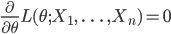
の解,もしくは,対数尤度を θ で微分して 0 とおいた,
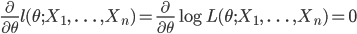
の解として得られる. (対数)尤度関数の微分が解析的に得られないときは,コンピュータで数値的に(対数)尤度関数の最大化を行う.
-
二項分布の成功確率の最尤推定
成功確率が p であるベルヌイ試行を n 回繰り返したところ成功回数が x であったとすると,その尤度と対数尤度は,
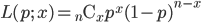
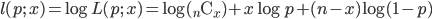
となる.これを最大にする p を求めるため,p で微分して 0 とおくと,
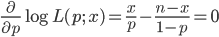
となる.その解を
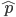
とおくと,
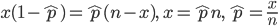
となり,最尤推定量が求まる.二項分布の場合の最尤推定量は解析的に簡単に求まるが,R では数値的に最尤推定値を求めることができる.
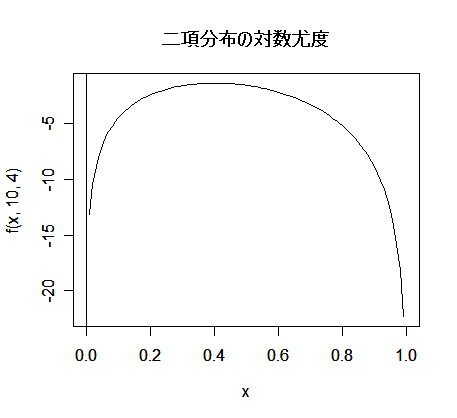
n = 10 回の試行で
x = 4 回成功したとすると,成功確率
p の最尤推定値は,
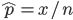
= 4/10 = 0.4 である.
# 二項分布の最尤推定値の R スクリプト
|
f <- function(x, n, y) y*log(x) + (n-y)*log(1-x)
| # 対数尤度を自分で定義 |
|
f <- function(x, n, y) dbinom(y, size=n, prob=x, log=T)
| # 二項分布確率関数の利用 |
|
curve(f(x, 10, 4), 0,1)
| # 対数尤度関数の表示 |
|
abline(h=0, v=0)
| # |
|
title(main="二項分布の対数尤度")
| # |
|
optimize(f, c(0.1, 0.9), maximum = T, n=10, y=4)
| # 対数尤度の最大値を取る点の探索 |
-
正規分布パラメータの最尤推定
平均 μ,分散 σ2 である正規分布 N(μ,σ2) からの無作為標本の実現値 x1,…,xn が得られたとすると,その尤度と対数尤度は
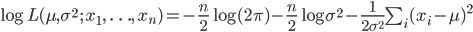
となる.これを最大にする μ と σ2 を求めるため,μ,σ2 で偏微分して 0 とおくと,
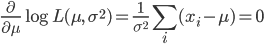
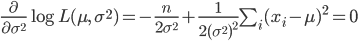
となる.その解を
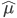
と
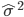
とおくと,
となり,最尤推定量が求まる.
正規分布の分散の最尤推定量は,標本不偏分散 s2,
ではない.
さてこのように,正規分布の場合の最尤推定量は解析的に簡単に求まるが,R では数値的に最尤推定値を求めることができる.
# 正規分布の最尤推定値の R スクリプト
|
n <- 10
| # サンプルサイズ |
|
y <- rnorm(n)
| # サンプルとして正規乱数を使用 |
|
f <- function(x){
| # 正規分布対数尤度関数の定義 |
|
m <- x[1]; s2 <- x[2]
| # 平均と分散 |
|
sum(dnorm(y, mean=m, sd=sqrt(s2), log=T))
| # 正規分布密度関数の対数(log=T) |
|
}
| # |
|
a <- optim(c(0.1,0.9), f, control=list(fnscale=-1, ndeps=1e-5))
| # 平均と分散の初期値で f を最大化(fnscale=-1) |
|
a$par
| # 最尤推定値(近似解)の表示 |
|
mean(y)
| # 平均の最尤推定値(真値) |
|
var(y)*(n-1)/n
| # 分散の最尤推定値(真値) |
|
m <- seq(-1, 1, length=50)
| # 平均の範囲指定 |
|
s2 <- seq(0.5, 2, length=50)
| # 分散の範囲指定 |
|
z <- matrix(0, nrow=length(m), ncol=length(s2))
| # (平均,分散)の行列 |
|
for(i in 1:length(m)){
| # |
|
for(j in 1:length(s2)) z[i,j] <- f(c(m[i],s2[j]))
| # 対数尤度値を z に格納 |
|
}
| # |
|
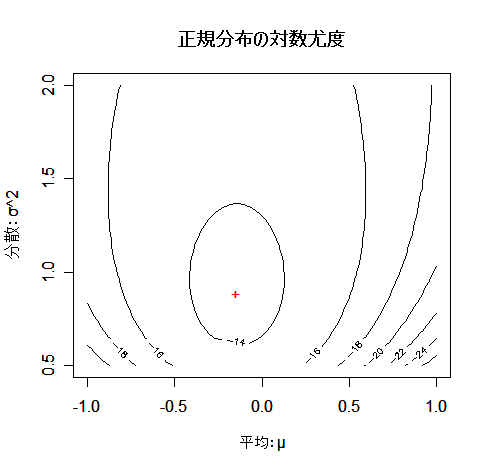
contour(m, s2, z, xlab="平均:μ", ylab="分散:σ^2")
| # 対数尤度の等高線表示 |
|
points(a$par[1], a$par[2], pch="+", col=2)
| # 最尤推定値の数値解の表示 |
|
title(main="正規分布の対数尤度")
| # |
-
カウント数データの尤度
カウント数データを生成する離散確率分布がパラメータを θ として,f(x ; θ) で表されるとする.カウント数 x = 0,1,2,…,r,に対して以下の表のようなデータが得られたとする.ただし,x = r + 1 に対しては, r + 1 以上のカウント数が得られた場合を集計している.このようなデータを打ち切り(censored)データという.すなわち,r + 1 以上のカウント数は出現頻度が低いので,一括してまとめられたものである.
打ち切りデータは,生存期間など,対象となる生物個体すべてが死亡するまで観測しないで,ある程度の期間観測した後,それ以降は,観測終了時の生存個体数を記録して観測を打ち切るような場合に生じる.
カウント数データ
| カウント数 x |
0 |
1 |
2 |
… |
r |
r + 1 以上 |
| 観測度数 y |
n0 |
n1 |
n2 |
… |
nr |
nr+1 |
上の表の尤度は,
![L(\theta \ ; \ y)=f(0; \theta)^{n_0} \cdot f(1;\theta)^{n_1} \cdots f(r; \theta)^{n_r} \cdot \Bigl[ \sum_{i=r+1}^{\infty} f(i;\theta) \Bigr]^{n_{r+1}}](images/EXTERN_0061.png)
と表せる.ここで,最後の項は n ≧ r + 1 以上のカウントが得られる確率を足し合わせた確率が nr+1 回生起したと考えて計算される尤度である.これより対数尤度は,
と表せる.これを最大にする θ を求めればよい.
-
負の二項分布パラメータの最尤推定
負の二項分布の紹介時に,
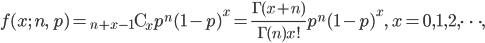
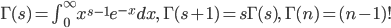
において,虫歯数データ
小学生1人あたりの虫歯数(再掲だが少し違う)
| 虫歯の数 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8以上 |
| 児童の数 |
4 | 9 |
16 | 13 |
9 | 7 |
5 | 4 |
3 |
に,モーメント法でパラメータを推定して負の二項分布をあてはめた.虫歯 8 以上を 8 とみなしてデータの平均を m = 3.3286,分散を v = 4.3063 と計算した.負の二項分布の平均と分散がデータの平均と分散と等しいと考え,
平均:
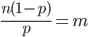
,分散:
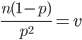
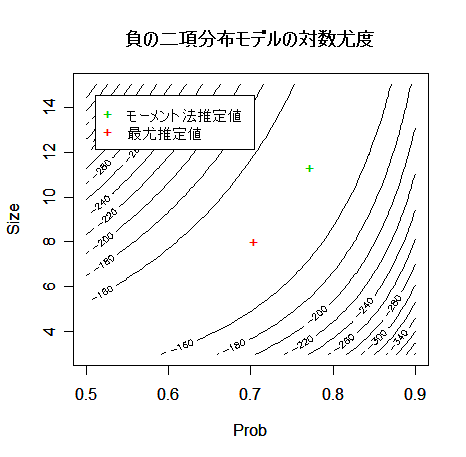
とおいた.これより,p = m/v = 0.7729,n = mp/(1 - p) = 11.3315,と推定された.ここでは,モーメント法による推定値を初期値として,パラメータの最尤推定を数値的に行ってみる.
# 負の二項分布の最尤推定値の R スクリプト
|
y <- c(4,9,16,13,9,7,5,4,3)
| # 虫歯データ |
|
xx <- 0 : (length(y) - 1)
| # 虫歯数 |
|
s <- sum(y)
| # |
|
m <- sum(xx*y/s)
| # 虫歯数平均 |
|
v <- sum((xx-m)^2*y/s)
| # 虫歯数分散 |
|
p0 <- m/v
| # 確率パラメータ(モーメント法) |
|
n0 <- m*p0/(1-p0)
| # サイズパラメータ(モーメント法) |
|
f <- function(x){
| # |
|
n <- x[1]; p <- x[2]
| # |
|
if(p<0) p <- 0.01
| # p が負のとき |
|
if(p>1) p <- 0.99
| # p が1を超えたとき |
|
r <- length(y)-2
| # |
|
q <- dnbinom(0:r, size=n, prob=p, log=T)
| # 負の二項分布の確率の対数 |
|
q[r+2] <- pnbinom(r, size=n, prob=p, lower.tail=F, log.p=T)
| # 負の二項分布 r 以上の確率の対数 |
|
sum(q*y)
| # カウント数の負の二項分布の対数尤度 |
|
}
| # |
|
a <- optim(c(n0, p0), f, control=list(fnscale=-1))
| # 対数尤度の最大値探索 |
|
a$par
| # 最尤推定値 |
|
p <- seq(0.5, 0.9, length=51)
| # 確率パラメータの離散値範囲 |
|
n <- seq(3, 15, length=51)
| # サイズパラメータの離散値範囲 |
|
z <- matrix(0, nrow=length(p), ncol=length(n))
| # 対数尤度値の格納行列 |
|
for(i in 1:length(p)){
| # |
|
for(j in 1:length(n)) z[i, j] <- f(c(n[j], p[i]))
| # 対数尤度値の格子点での計算 |
|
}
| # |
|
contour(p, n, z, xlab="Prob", ylab="Size")
| # 等高線表示 |
|
points(a$par[2], a$par[1], pch="+", col=2)
| # 最尤推定値の表示 |
|
points(p0, n0, pch="+", col=3)
| # モーメント推定値の表示(初期値) |
|
legend(0.51, 14.5, c("モーメント法推定値","最尤推定値"), bg="white", pch="+", col=3:2)
|
|
title(main="負の二項分布モデルの対数尤度")
| # |
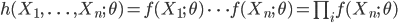
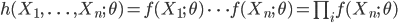
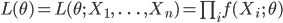
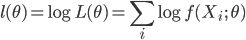
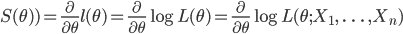
 の近傍で負となる( L(θ) が上に凸)となるので,この関数を
の近傍で負となる( L(θ) が上に凸)となるので,この関数を
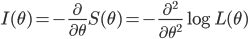
![{\cal I}(\theta) = {\rm E}_\theta[I(\theta)]=-{\rm E}_\theta \Bigl[\frac{\partial^2}{\partial \theta^2} \log L(\theta) \Bigr]](images/EXTERN_0006.png)
![= \mathrm{E}_\theta \Bigl[ \{ \frac{\partial}{\partial \theta} \log L(\theta) \}^2 \Bigr]](images/EXTERN_0007.png)
 のもとでのこの関数の値
のもとでのこの関数の値 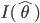 を Fisher 情報量 (observed Fisher Information) ということもある.一般に,
を Fisher 情報量 (observed Fisher Information) ということもある.一般に,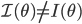 であるが,正規分布やポアソン分布などの指数分布族では
であるが,正規分布やポアソン分布などの指数分布族では 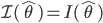 である.
である.
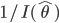 が
が  の分散の近似推定値になる.すなわち,
の分散の近似推定値になる.すなわち,
![{\rm Var} [\hat{\theta}] \approx \frac{1}{I(\hat{\theta})}, \quad \ {\rm se}(\hat{\theta}) \approx I(\hat{\theta})^{-1/2](images/EXTERN_0013.png)
 ) は
) は  の標準誤差 (standrad error) である.
の標準誤差 (standrad error) である.
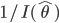 が
が  の分散に一致することを示す.
の分散に一致することを示す.
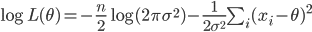
![S(\theta) =\frac{\partial}{\partial \theta} \log L(\theta) = -\frac{\partial}{\partial \theta} \Bigl[-\frac{n}{2}\log(2\pi \sigma^2)-\frac{1}{2\sigma^2}\sum_i(x_i-\theta)^2 \Bigr]](images/EXTERN_0015.png)
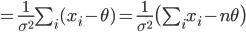
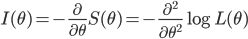
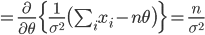
![{\cal I}(\theta) = {\rm E}_\theta[I(\theta)]= {\rm E}_\theta \bigl[ \frac{n}{\sigma^2} \bigr] = \frac{n}{\sigma^2}](images/EXTERN_0019.png)
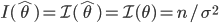 となる.一方,標本平均の分散は σ2/n なので,
となる.一方,標本平均の分散は σ2/n なので,
![{\rm Var}[\hat{\theta}] = {\rm Var}[\bar{x}] = \frac{\sigma^2}{n} =\frac{1}{I(\hat{\theta})](images/EXTERN_0021.png)
 と表記し,これを推定量(estimator)と呼ぶ.推定量は確率変数の関数(推定関数)で,統計量で構成される.標本の観測値が得られたときの推定量の実現値を推定値(estimate)と呼んで区別することもある.
と表記し,これを推定量(estimator)と呼ぶ.推定量は確率変数の関数(推定関数)で,統計量で構成される.標本の観測値が得られたときの推定量の実現値を推定値(estimate)と呼んで区別することもある.
![{\rm Pr}[ \hat{\theta}_1 < \theta < \hat{\theta}_2] = p, \ 0<p<1](images/EXTERN_0022.png)
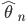 を構成したとする.このとき,標本の大きさ n を大きくしていけば母集団母数 θ を正しく推定できることが必要であろう.つまり,任意の ε > 0 に対して,
を構成したとする.このとき,標本の大きさ n を大きくしていけば母集団母数 θ を正しく推定できることが必要であろう.つまり,任意の ε > 0 に対して,
![\lim_{n \to \infty} {\rm Pr[ \ |\hat{\theta}_n - \theta | < \varepsilon \ ] =1](images/EXTERN_0024.png)
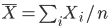 は母集団平均の一致推定量であることがわかる.
は母集団平均の一致推定量であることがわかる.
![{\rm MSE}(\theta)={\rm E}[ (T-\theta})^2 ] = {\rm E}[ ( t(X_1, \ \ldots \, X_n)-\theta)^2 ]](images/EXTERN_0026.png)
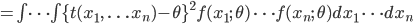
![{\rm MSE}(\theta) = {\rm E}[(T-\theta)^2 ] = {\rm E}[ \{(T-{\rm E}[T])-({\rm E}[T]-\theta) \}^2 ]](images/EXTERN_0028.png)
![={\rm E}[(T-{\rm E}[T])^2] + {\rm E}[ ({\rm E}[T]-\theta)^2 ]={\rm Var}[T]+(\theta-{\rm E}[T])^2](images/EXTERN_0029.png)
![{\rm E}[T]=\theta](images/EXTERN_0030.png)
![{\rm E}[\bar{X}] = {\rm E} \bigl[ \frac{1}{n} \sum_i X_i \bigr] = \frac{1}{n} \sum_i {\rm E}[X_i]=\frac{1}{n}n \mu=\mu](images/EXTERN_0031.png)
![{\rm Var}[\bar{X}] ={\rm Var} \bigl[ \frac{1}{n} \sum_i X_i \bigr] = \frac{1}{n^2}\sum_i {\rm Var}[X_i]=\frac{1}{n^2} n\sigma^2=\frac{\sigma^2}{n}](images/EXTERN_0032.png)
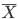 としたとき,
としたとき,
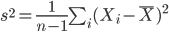
![{\rm E}[s^2] = {\rm E} \Bigl[ \frac{1}{n-1} \sum_i(X_i-\bar{X})^2 \Bigr]=\frac{1}{n-1} {\rm E}[
\sum(X_i-\mu)^2-n(\bar{X}-\mu)^2]](images/EXTERN_0035.png)
![=\frac{1}{n-1} \bigl{ \sum {\rm E}[(X_i-\mu)^2]-n{\rm E}[(\bar{X}-\mu)^2] \bigr} = \frac{1}{n-1} \bigl{\sum {\rm Var}[X_i]-n{\rm Var}[\bar{X}] \bigr}](images/EXTERN_0036.png)
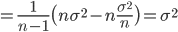
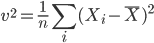

![{\rm Var}[T] \geq \frac{[\tau'(\theta)]^2}{ \calI (\theta)}](images/EXTERN_0039.png)
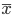 の分布は,
の分布は,
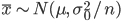
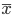 は不偏である.分散既知の正規分布では,大きさ n の無作為標本の Fisher 情報量は,前節の結果より,
は不偏である.分散既知の正規分布では,大きさ n の無作為標本の Fisher 情報量は,前節の結果より,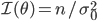 であり,
であり,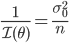
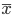 の分散に一致する.よって,標本平均は分散既知の正規母集団の平均に対する有効な推定量,すなわち,最良であることがわかる.
の分散に一致する.よって,標本平均は分散既知の正規母集団の平均に対する有効な推定量,すなわち,最良であることがわかる.
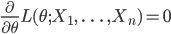
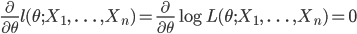
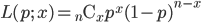
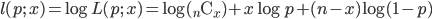
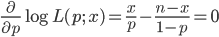
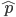 とおくと,
とおくと,
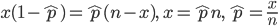
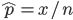 = 4/10 = 0.4 である.
= 4/10 = 0.4 である.
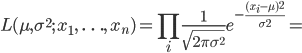
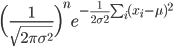
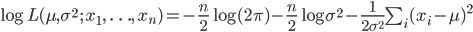
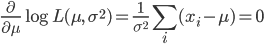
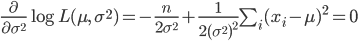
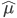 と
と 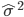 とおくと,
とおくと,
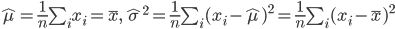
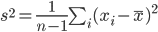
![L(\theta \ ; \ y)=f(0; \theta)^{n_0} \cdot f(1;\theta)^{n_1} \cdots f(r; \theta)^{n_r} \cdot \Bigl[ \sum_{i=r+1}^{\infty} f(i;\theta) \Bigr]^{n_{r+1}}](images/EXTERN_0061.png)
![\log L(\theta; y)=n_0 \log f(0; \theta) + n_1 \log f(1; \theta) + \ \cdots \ + n_r \log f(r; \theta) +n_{r+1} \log \Bigl[ \sum_{i=r+1}^{\infty} f(i; \theta) \Bigr]](images/EXTERN_0062.png)
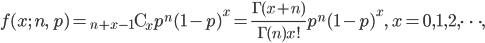
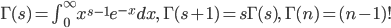
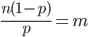 ,分散:
,分散: