![{\rm Pr} \Bigl[ -1.96 < \frac{\sqrt{n}(\bar{x}-\mu)}{\sigma} < 1.96 \Bigr] = 0.95](images/EXTERN_0005.png)
統計学で扱う仮説(hypothesis)とは,母集団に対する断定や推測.たとえば,
統計的仮説検定で用いられる仮説は,まず,帰無仮説(null hypothesis)という形式で与えられる.
帰無仮説は棄却(reject)されることに意味がある仮説である.
帰無仮説と反対の仮説を対立仮説(altanative hypothesis)という.
上の3番目の例でみると,
母集団 A と母集団 B は異なる処理(薬の投与など)をしているので,実験の目的 は,母集団 A と母集団 B の平均は異なる(処理効果がある)ことを言いたい (対立仮説が正しいことを望む)のだが,まずは 「等しい(処理効果無し)」と仮定してみようという考え方で, 数学の背理法と似た論理である.
背理法:√2 が無理数であることを証明するため,まず√2 が有理数であると仮定し,矛盾があることを 示す.つまり,有理数であることは絶対ありえない(確率 0 である!)ことを示す. この矛盾は,そもそも√2 を有理数とした仮定が誤っていたからであると考え,有理数という仮定を 棄却して,無理数であることを証明する.
統計的仮説検定では,たとえば2つの母集団平均が等しいという帰無仮説を考えると,
この帰無仮説のもとで,検定統計量(標本平均の差に基づく t 値など)以上
(もしくは未満)の値が得られる確率を求める.R ではこの値が p 値で表示される.
p 値は
くだけた言い方をすれば,帰無仮説が正しいとしたときに,標本のようなデータが得られる確率
である.
これが十分小さい(ほとんどありえない)ときは,平均が等しいと仮定したことが誤りであったと判断して
帰無仮説を棄却し,2つの母集団平均には差があると結論づける.
この確率がそれほど小さく
ない場合は,このような統計量が得られることもありえると考え,帰無仮説を採択し,平均が等しいと考え
てもよいとする.
棄却か採択かの判断の基準となる確率を有意水準といい,
5 % や 1 % がよく用いられる.
統計のソフトが発達していなかった頃は,検定統計量である t 値や F 値を電卓等で算出し,その値を
t 分布や F 分布の 5 %や 1 %の有意水準に対応する数表と照らし合わせて検定を行い,5 %有意とかを
記述していた.
現在では,ソフトが検定統計量に対する p 値を直接計算してくれるので数表はいらなくなった.この結果,
検定に重要な数字であった t 値や F 値より,より直接的な p 値が重要な指標になってきた.p 値を
みれば,何%有意かが一目でわかるので,結果にわざわざ 5 %有意とかを記述する必要がなくなってきており,
論文の書き方も変わってきている.
実験状況によっては,薬投与などの処理を行った集団(処理群)平均 μA が,薬を投与しない 集団(対照群)の平均 μB より小さくなることはないことが事前に わかっているような場合が ある.このようなとき,
母集団平均に対する両側検定は,母集団平均に対する信頼区間と大きな関係がある. いま,帰無仮説(H0)と対立仮説(H1)が,
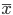 であったとすると,母平均μに対する
95%信頼区間は,
であったとすると,母平均μに対する
95%信頼区間は,
![{\rm Pr} \Bigl[ -1.96 < \frac{\sqrt{n}(\bar{x}-\mu)}{\sigma} < 1.96 \Bigr] = 0.95](images/EXTERN_0005.png)
![{\rm Pr} \bigl[ \bar{x} - 1.96 \cdot\frac{\sigma}{\sqrt{n}} < \mu < \bar{x} + 1.96 \cdot\frac{\sigma}{\sqrt{n}} \Bigr]](images/EXTERN_0006.png)
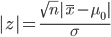
| 帰無仮説を受諾 ⇔ |
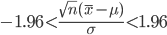
|
検定は,仮説を棄却するか採択するかのいずれかであるが,
統計量は分布をもつので,この判定には間違いが起こることがある.
以下のように,この過誤には
2 種類がある.
| 仮説の棄却(reject) | 仮説の採択(accept) | |
|---|---|---|
| 仮説が真(true)のとき | 第1種の過誤(Type 1 error) | 正解 |
| 仮説が偽(false)のとき | 正解 | 第2種の過誤(Type 2 error) |
第1種の過誤が有意水準である.また,第2種の過誤の確率を β としたとき, 仮説が偽のとき正しく仮説を棄却する確率,1 - β,を検出力,もしくは検定力(power)という. よい検定は,第1種の過誤を固定したもとで検出力の高い検定方式である.
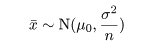
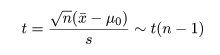
なお,この検定は,対のある標本に適用できる.対のある標本とは,n 組のペアー標本(paired smple),
文献
| engei <- read.csv("engei.csv") | # csv データ読み込み |
| engei | # データの表示 |
| x <- engei[,3] | # 園芸療法前の MSE 得点を x に格納(列数で指定) |
| x <- engei$療法前 | # 園芸療法前の MSE 得点を x に格納(変数名で指定) |
| y <- engei$療法後 | # 園芸療法後の MSE 得点を x に格納(変数名で指定) |
| t.test(y, x, paired=TRUE) | # 1母集団 t 検定,paired = TRUE で対標本を指定 |
| d <- y - x | # 療法後 − 療法前で療法の効果をみる |
| d | # 療法の効果の表示 |
| t.test(d) | # 1母集団 t 検定,先ほどと同じ検定 |
| n <- length(d) | # 標本の大きさ(サンプルサイズ) |
| mean(d) | # 標本平均 |
| sd(d) | # 標本標準偏差 |
| dv <- n - 1 | # 標本の自由度 |
| t <- sqrt(n)*mean(d)/sd(d) | # 効果がないとの帰無仮説のもとでの t 値 |
| t | # 検定統計量 t 値の表示 |
| 2*(1 - pt(t, df=dv)) | # 両側検定の p 値 |
| t0 <- qt(0.975, df=dv) | # 両側 5 %検定の閾値 |
| dw <- t0*sd(d)/sqrt(n) | # 95%信頼区間の幅 |
| mean(d)-dw | # 95%信頼区間の下限 |
| mean(d)+dw | # 95%信頼区間の上限 |
| t.test(d, alternative="greater") | # 片側検定 |
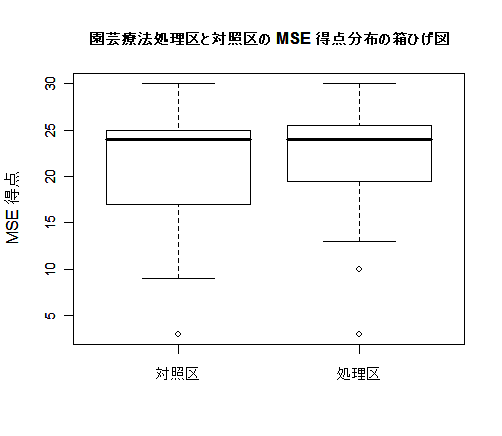
このデータでは,クライアント全体では園芸療法の効果は認められなかった.また,MSE の満点が30点なので, 元々心理機能に問題がなく満点近い得点のクライアントでは,効果が認められないのも当然といえる. その上,園芸療法処方の前後で半年 程度のタイムラグがあるので,何もしなくても認知症の症状が進行する場合もあり,効果が検出しずらい こともある程度予測できる.
課題: クライアントのうち若年層( 85 歳以下)を取り出し,園芸療法の効果を検定せよ.
| N <- 10000 | # シミュレーション回数 |
| n <- 10 | # サンプルサイズ |
| n1 <- rnorm(N*n, mean=10, sd=2) | # N(10, 4) から大きさ n の標本を N 回シミュレーション |
| n1.mat <- matrix(data=n1, ncol=n) | # データ行列 |
| n1.mean <- apply(n1.mat, 1, mean) | # 各サンプルの平均 |
| n1.var <- apply(n1.mat, 1, var) | # 各サンプルの分散 |
| n1.var3 <- n1.var/n | # 各標本平均の分散 |
| n1.td <- (n1.mean - 10)/sqrt(n1.var3) | # 各サンプルの t 値 |
| mean(n1.td) | # t 値の平均 |
| sd(n1.td) | # t 値の標準偏差 |
| mt <- ceiling(max(abs(n1.td))) | # t 値の絶対値の最大値 |
| xq1 <- qt(0.025, df = (n-1)) | # t(9) の 2.5% 点 |
| xq2 <- qt(0.975, df = (n-1)) | # t(9) の 97.5% 点 |
| length( n1.td[abs(n1.td) > xq2]) | # 5% 検定で有意となった個数 |
| hist(n1.td, breaks=seq(-mt, mt, by=0.2), probability=TRUE, xlab="t 値", ylab="密度", main="") | |
| abline(v=xq1, col="red") | # 採択域の下限 |
| abline(v=xq2, col="red") | # 採択域の上限 |
| #curve(dt(x, df=(n-1)), -6, 6, add=T, col="red") | # t(9) の表示 |
| title(main="t 値のヒストグラムと有意となった個数") | # タイトル |
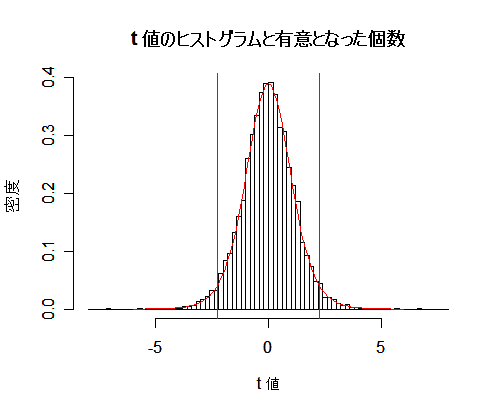
n <- 10 # サンプルサイズ m0 <- 10 # 帰無仮説の平均 s <- 2 # 標準偏差 m <- 11 # 真の平均 delta <- sqrt(n)*(m-m0)/s # 非心度 curve(dt(x, df=(n-1)), -4,7) curve(dt(x, df=(n-1), ncp=delta), -4,7, col="red", add=T) title(main="non-central t distribution") |
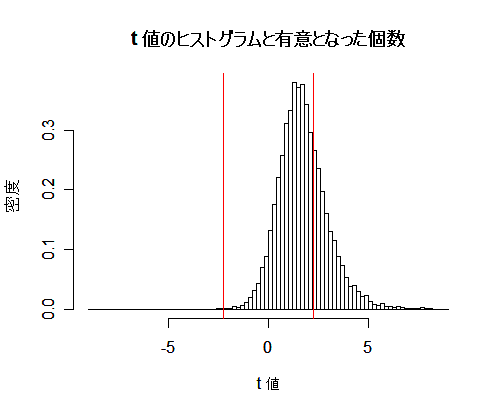
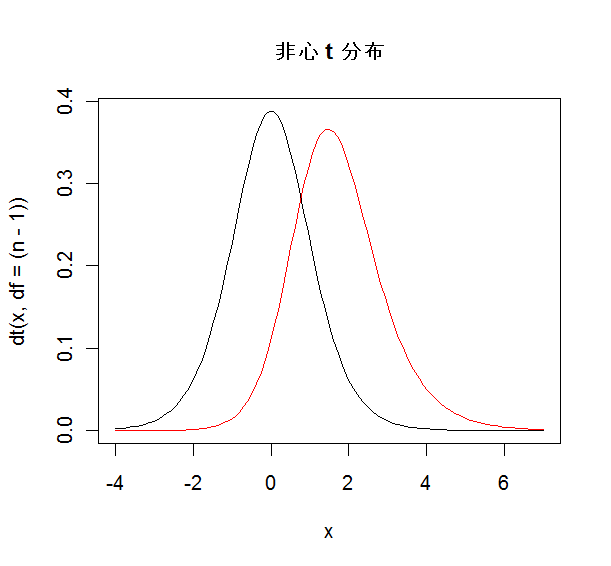
| m <- 11 | # 母集団平均(帰無仮説が偽の場合) |
| n1 <- rnorm(N*n, mean=m, sd=2) | # N(m, 4) から大きさ n の標本を N 回シミュレーション |
課題1::母集団平均を m = 12 としたときの検出力を求めよ.
課題2::真の母集団平均が μ = 11 であるとき,検出力を 90%程度にするために 必要なサンプルサイズを求めよ.
2つの母集団 A,B があり,それぞれが平均を μA,μB, 分散を σA2,σB2 の正規分布に従って いるが,その値は未知であるとする.いま,両集団の分散の値が等しく, σA2=σB2=σ2,と仮定 できるとしよう.このとき,2つの母平均に対する
母集団 A から大きさ nA,母集団 B から大きさ nB の標本を抽出した. 母集団 A からの標本の標本平均が x-A, 標本分散が sA2 であり,母集団 B の 標本平均が x-B, 標本分散が sB2 であった.母集団 A,B が共通の 分散 σ2 をもつとすると,その推定値 s2 は 以下のように推定できる.
| 母集団 A からの標本の偏差平方和: | SA=(nA−1)sA2 |
| 母集団 B からの標本の偏差平方和: | SB=(nB−1)sB2 |
| 母集団 A,B 全体での偏差平方和: | S = SA + SB =(nA−1)sA2+ (nB−1)sB2 |
| 母集団 A,B 共通の標本分散: |
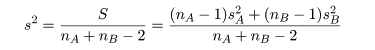
|
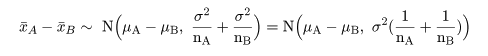
帰無仮説(H0: μA = μB)のもとでは,μA−μB=0,なので, 標本平均の差は,
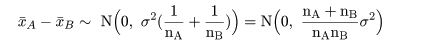
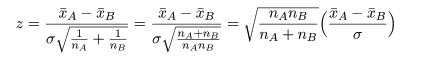
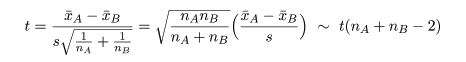
母集団A,Bで分散の同等性が疑われるときは,ウェルチ(Welch)の検定を用いる.
| engei <- read.csv("engei.csv") | # csv データ読み込み |
| x <- engei$療法前 | # 園芸療法前の MSE 得点を x に格納(変数名で指定) |
| y <- engei$療法後 | # 園芸療法後の MSE 得点を y に格納(変数名で指定) |
| boxplot(x, y, names= c("対照区","処理区"), ylab="MSE 得点", cex.axis=0.8) | |
| title(main="園芸療法処理区と対照区の MSE 得点分布の箱ひげ図", cex.main=1.0) | |
| t.test(y, x, var.equal=T) | # 2標本 t 検定 |
| mx <- mean(x) | # 対照区平均 |
| my <- mean(y) | # 処理区平均 |
| nx <- length(x) | # 対照区サンプルサイズ |
| ny <- length(y) | # 処理区サンプルサイズ |
| dfv <- nx+ny-2 | # データの自由度 |
| vx <- var(x) | # 対照区標本分散 |
| vy <- var(y) | # 処理区標本分散 |
| v <- ((nx-1)*vx + (ny-1)*vy)/dfv | # こみにした共通の分散 |
| d <- my - mx | # 処理区平均 − 対照区平均 |
| vd <- v/nx + v/ny | # 処理平均の差の分散 |
| tv <- d/sqrt(vd) | # t 値 |
| 2*(1 - pt(abs(tv), df=dfv)) | # p 値 |
| t0 <- qt(0.975, df=dfv) | # 自由度 dfv の t 分布の97.5%点 |
| dw <- t0*sqrt(vd) | # 95 %信頼区間の幅 |
| d - dw | # 平均の差の 95%信頼区間の下限 |
| d + dw | # 平均の差の 95%信頼区間の上限 |
| t.test(x, y) | # ウェルチ(Welch)の検定 |
課題: クライアントのうち若年層( 85 歳以下)を取り出し,2標本 t 検定を行え.
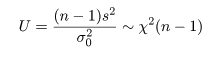
有意水準 5 %の検定は,自由度 n - 1 の χ2 分布の 2.5%点と 97.5%点をそれぞれ χ2(n - 1)0.025, χ2(n - 1)0.975 とすると,
母集団 A から大きさ nA,母集団 B から大きさ nB の標本を抽出した. 母集団 A からの標本の標本平均が x-A, 標本分散が sA2 であり,母集団 B の 標本平均が x-B, 標本分散が sB2 であるとする.すると, 標本分散に関係した量はそれぞれ
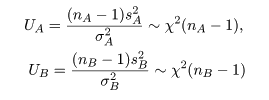
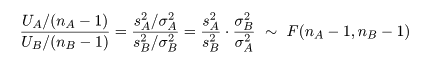
ところで,帰無仮説が正しいとする と,σA2 = σB2 とおけるので, 母集団の分散比は,γ0 = σA2/σB2 = 1, となる.このとき,標本分散の分散比の統計量 γ が,
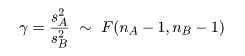
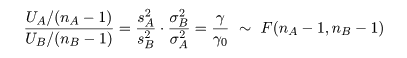
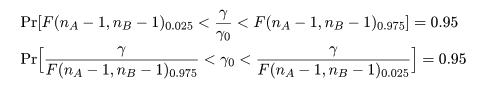
| engei <- read.csv("engei.csv") | # csv データ読み込み |
| x <- engei$療法前 | # 園芸療法前の MSE 得点を x に格納(変数名で指定) |
| y <- engei$療法後 | # 園芸療法後の MSE 得点を y に格納(変数名で指定) |
| var(x) | # 対照区の標本分散 |
| var(y) | # 処理区の標本分散 |
| var.test(x, y) | # 分散の等質性の検定 |
課題: 分散の等質性検定で表示される数値を R の基本統計関数を用いて出せ.
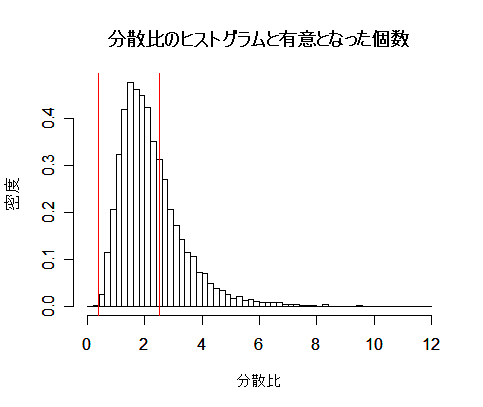
| N <- 10000 | # シミュレーション回数 |
| n <- 20 | # サンプルサイズ |
| s1 <- 1; s2 <- 2 | # 母集団分散(分散比 = 2) |
| n1 <- rnorm(N*n, mean=0, sd=sqrt(s1)) | # 正規乱数 |
| n2 <- rnorm(N*n, mean=0, sd=sqrt(s2)) | # 正規乱数 |
| n1.mat <- matrix(data=n1, ncol=n) | # N×n データ行列(母集団1) |
| n1.var <- apply(n1.mat, 1, var) | # 各行の分散 |
| n2.mat <- matrix(data=n2, ncol=n) | # N×n データ行列(母集団2) |
| n2.var <- apply(n2.mat, 1, var) | # 各行の分散 |
| ratio <- n2.var/n1.var | # 分散比 |
| f0 <- qf(0.025, df1=(n-1), df2=(n-1)) | # F 分布2.5%点 |
| f1 <- qf(0.975, df1=(n-1), df2=(n-1)) | # F 分布97.5%点 |
| m0 <- length(ratio[ratio < f0]) | # 2.5%以下の個数 |
| m1 <- length(ratio[ratio > f1]) | # 97.5%以下の個数 |
| m0+m1 | # 帰無仮説を棄却した個数 |
| mf <- ceiling(max(ratio)) | # 分散比の最大値 |
| hist(ratio, breaks=seq(0, mf, by=0.2), probability=TRUE, xlab="分散比", ylab="密度", main="") | |
| abline(v=f0, col="red") | # F 分布2.5%点の表示 |
| abline(v=f1, col="red") | # F 分布97.5%点の表示 |
| title(main="分散比のヒストグラムと有意となった個数") | # |
課題: 淡水性ウナギの汽水域での生理活性の違いのデータ、ウナギデータ, を2標本データとして違いを検定せよ.ただし,2母集団で分散の違いがあるようなので,まず, 分散の同等性の検定を行い,違いが認められるときは,データの対数変換を行うなどして,分散安定化 変換を行って t 検定を行ってみよ.また,データの対数変換などを行わず.ウェルチ検定やノンパラメトリック 検定を行った場合との比較検討を行え.
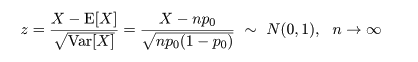
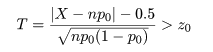
このように,中心極限定理を利用して,標準正規近似を行って検定を行うやり方を大標本(large sample)理論 といい,コンピュータが発達する以前はもっぱら大標本理論に基づいた検定を行っていた.
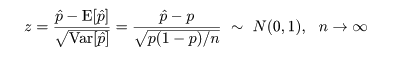
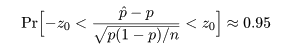
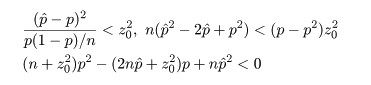
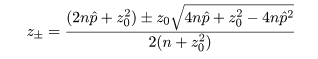
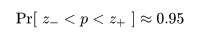
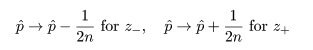
ここで,さらに近似を加えて,z02 の項を消去すると, p の2次方程式の根は,
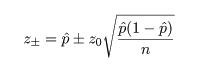
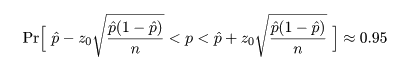
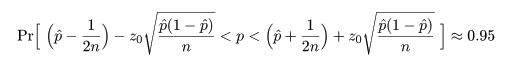
ところで,正規近似による信頼区間の構成では,場合により信頼区間が負になったり 1 を超えることがあるが, このときは,0 と 1 で切り詰め(truncate)る.
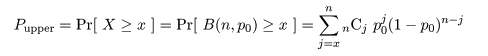
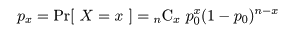
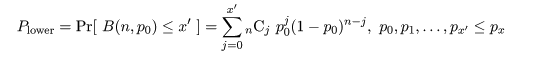
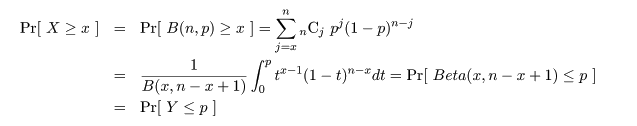
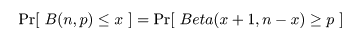
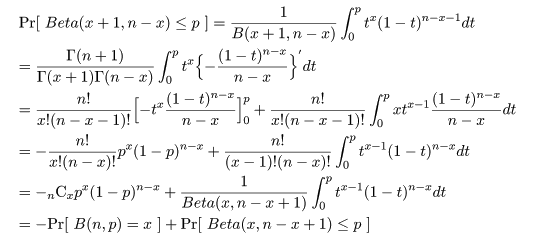
これより,成功確率 p の 95%信頼区間は,
ところで,F 分布とベータ分布の関係
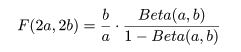
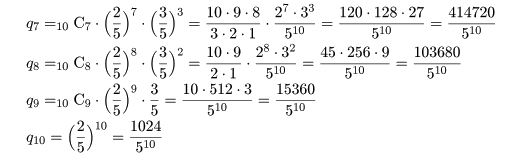
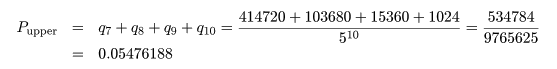
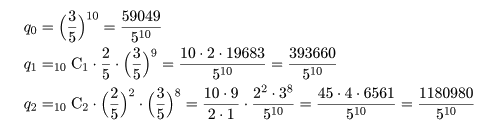
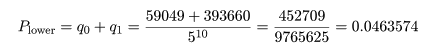
binom.test(7, 10, p=0.4) # 二項確率に基づく正確な検定 up <- 1 - pbinom(6, 10, prob=0.4); up # 上側確率 pbinom(6, 10, prob=0.4, lower.tail=F) # 上側確率 lp <- pbinom(1, 10, prob=0.4); lp # 下側確率 lp + up # 両側検定 p 値 binom.test(7, 10, p=0.4, alternative="greater") # 片側検定(H1 : p > 0.4) up # 片側検定 p 値 binom.test(7, 10, p=0.4, alternative="less") # 片側検定(H1 : p < 0.4) pbinom(7, 10, prob=0.4) # 片側検定 p 値 |
| r <- 7; n <- 10 | # 成功回数と試行回数 |
| prop.test(r, n, p=0.5, correct=F) | # H0:p = 0.5 の正規近似検定(補正なし) |
| prop.test(r, n, p=0.5) | # H0:p = 0.5 の正規近似検定(連続性の補正) |
| binom.test(r, n, p=0.5) | # 二項確率に基づく正確な検定 |
課題: 試行回数を増やして(n = 30)同様な検定を行え.
課題:ある調査会社によると,NHK 大河ドラマの関東地区世帯視聴率は24.5%であった. 真の世帯視聴率の 95 %信頼区間を求めよ.
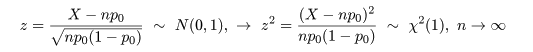
| 成 功 | 失 敗 | |
|---|---|---|
| 観測度数 | X | n - X |
| 期待度数 | np0 | n(1 - p0) |
となる.ここで,ピアソン(Pearson)のχ2 値,

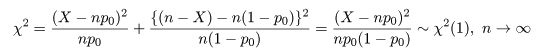
| r <- 7; n <- 10 | # 成功回数と試行回数 |
| x <- c(r, n-r) | # 成功回数と失敗回数のベクトル |
| p0 <- c(0.5, 0.5) | # 成功確率と失敗確率の帰無仮説 |
| chisq.test(x, p=p0) | # ピアソン χ2 適合度検定 |
| セル1 | セル2 | セル3 | セル4 | セル5 | 計 | |
|---|---|---|---|---|---|---|
| 観測度数 | n1 | n2 | n3 | n4 | n5 | n |
| 想定確率分布 | p1 | p2 | p3 | p4 | p5 | 1 |
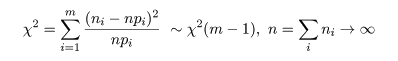
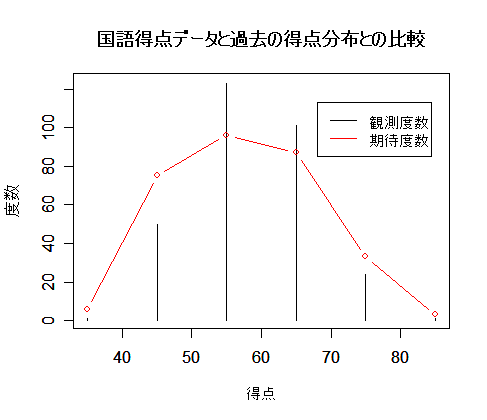
| 得 点 | 30〜39 | 40〜49 | 50〜59 | 60〜69 | 70〜79 | 80〜89 |
|---|---|---|---|---|---|---|
| 人 数 | 1 | 50 | 123 | 101 | 24 | 1 |
| 過去の確率分布 | 0.02 | 0.25 | 0.32 | 0.29 | 0.11 | 0.01 |
| x <- c(35, 45, 55, 65, 75, 85) | # 階級の代表値 |
| y <- c(1, 50, 123, 101, 24, 1) | # 観測度数 |
| p0 <- c(0.02, 0.25, 0.32, 0.29, 0.11, 0.01) | # 過去の確率分布 |
| chisq.test(y, p=p0) | # χ2 適合度検定 |
| s <- sum(y) | # |
| plot(x, y, type="h", xlab="得点", ylab="度数") | # 観測度数のグラフ |
| points(x, s*p0, type="b", col="red") | # 期待度数のグラフ |
| legend(68,113, c("観測度数", "期待度数"), lty=1, col=c("black","red")) | |
| title(main="国語得点データと過去の得点分布との比較") | # |
| 成功回数 | 0 回 | 1 回 | 2 回 | 3 回 | 4 回 | 5 回 | 6 回 | 計 |
|---|---|---|---|---|---|---|---|---|
| 期待観測度数 | 8.8 | 26.3 | 32.9 | 22.0 | 8.2 | 1.7 | 0.1 | 100 |
| N <- 10000 | # シミュレーション回数 |
| m <- 6 | # 試行1回でのベルヌイ試行の数 |
| n <- 100 | # 二項確率の試行数 |
| p0 <- dbinom(x=0:6, size=6, p=1/3) | # 二項確率 B(6, 1/3) |
| w <- rbinom(n, m, p=1/3) | # n = 100 回の試行での成功回数(観測値)の系列) |
| tw <- table(factor(w,levels=0:m)) | # 成功回数の表(データ) |
| r <- chisq.test(tw, p=p0) | # データと二項確率との適合度検定 |
| p1 <- c(p0[1:4], p0[5]+p0[6]+p0[7]) | # 少ない確率をまとめた二項確率 |
| y <- NULL | # χ2 値のベクトル |
| for(i in 1:N){ | # |
| w <- rbinom(n, m, p=1/3) | # n = 100 回の試行での成功回数(観測値)の系列) |
| fw <- table(factor(w,levels=0:m)) | # 成功回数の表(データ) |
| tw <- c(fw[1:4], fw[5]+fw[6]+fw[7]) | # 成功回数 5,6,7 をまとめる |
| r <- chisq.test(tw, p=p1) | # 適合度検定の χ2 値 |
| y <- c(y, r$statistic) | # |
| } | # |
| my <- ceiling(max(y)) | # y の最大値を超える最小の整数 |
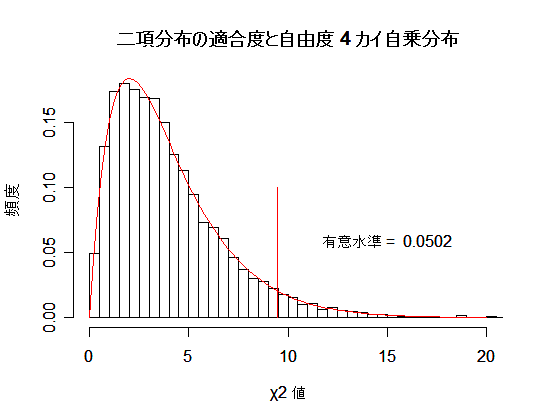
| mean(y) | # 平均(真値 = 4) |
| var(y) | # 分散(真値 = 8) |
| hist(y, breaks=seq(0,my,by=0.5),freq=FALSE,xlim=c(0,20),xlab="χ2 値",ylab="頻度",main="") | |
| x <- seq(0,20, by=0.1) | # |
| curve(dchisq(x, 4), 0, 20, add=T, col=2) | # 自由度 4 χ2 分布 |
| title(main="二項分布の適合度と自由度 4 カイ自乗分布") | # |
| q0 <- qchisq(0.95,df=4) | # χ2(4) の 95%点 |
| segments(q0,0, q0,0.1, col="red") | # 棄却域 |
| pv <- length(y[y>q0])/N | # |
| s <- paste("有意水準 = ", pv) | # 帰無仮説の棄却率(真値 = 0.05) |
| text(15,0.06, s) | # |
| セル1 | セル2 | セル3 | セル4 | セル5 | 計 | |
|---|---|---|---|---|---|---|
| 観測度数 | n1 | n2 | n3 | n4 | n5 | n |
| 推定確率分布 | p^1 | p^2 | p^3 | p^4 | p^5 | 1 |
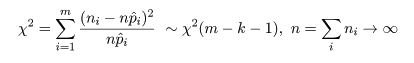
| 成功回数 | 0 回 | 1 回 | 2 回 | 3 回 | 4 回 | 5 回 | 6 回 | 計 |
|---|---|---|---|---|---|---|---|---|
| 観測度数 | 12 | 18 | 25 | 32 | 13 | 0 | 0 | 100 |
| N <- 10000 | # シミュレーション回数 |
| m <- 6 | # 試行1回でのベルヌイ試行の数 |
| n <- 100 | # 二項確率の試行数 |
| y <- NULL | # χ2 値のベクトル |
| for(i in 1:N){ | # |
| w <- rbinom(n, m, p=1/3) | # n = 100 回の試行での成功回数(観測値)の系列) |
| pd <- mean(w)/m | # データのもとでの推定成功確率 |
| p0 <- dbinom(x=0:6, size=6, p=pd) | # 推定成功確率のもとでの二項確率分布 |
| p1 <- c(p0[1:4], p0[5]+p0[6]+p0[7]) | # 少ない確率をまとめた二項確率 |
| fw <- table(factor(w,levels=0:m)) | # 成功回数の表(データ) |
| tw <- c(fw[1:4], fw[5]+fw[6]+fw[7]) | # 成功回数 5,6,7 をまとめる |
| r <- chisq.test(tw, p=p1) | # 適合度検定の χ2 値 |
| y <- c(y, r$statistic) | # |
| } | # |
| my <- ceiling(max(y)) | # y の最大値を超える最小の整数 |
| mean(y) | # 平均(真値 = 4) |
| var(y) | # 分散(真値 = 8) |
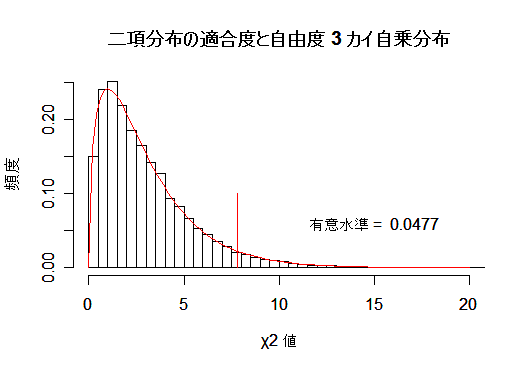
| hist(y, breaks=seq(0,my,by=0.5),freq=FALSE,xlim=c(0,20),xlab="χ2 値",ylab="頻度",main="") | |
| x <- seq(0,20, by=0.1) | # |
| curve(dchisq(x, 3), 0, 20, add=T, col=2) | # 自由度 3 χ2 分布 |
| title(main="二項分布の適合度と自由度 3 カイ自乗分布") | # |
| q0 <- qchisq(0.95,df=3) | # χ2(3) の 95%点 |
| segments(q0,0, q0,0.1, col="red") | # 棄却域 |
| pv <- length(y[y>q0])/N | # |
| s <- paste("有意水準 = ", pv) | # 帰無仮説の棄却率(真値 = 0.05) |
| text(15,0.06, s) | # |
| 5,6の個数 | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| 出た回数 | 185 | 1149 | 3265 | 5475 | 6114 | 5194 |
| 5,6の個数 | 6 | 7 | 8 | 9 | 10 以上 | 合計 |
| 出た回数 | 3067 | 1331 | 403 | 105 | 18 | 26306 |
| x <- 0:10 | # 5,6の個数 |
| y <- c(185,1149,3265,5475,6114,5194,3067,1331,403,105,18) | # 出た回数 |
| m <- sum(x*y)/sum(y) | # 出た回数の平均 |
| pd <- m/12 | # 5,6 の出る確率の推定値 |
| p <- dbinom(x=0:12, size=12, p=1/3) | # 正しいサイコロ(p = 1/3)のときの確率分布 |
| p0 <- c(p[1:10], p[11]+p[12]+p[13]) | # 出る回数 10 回以上をまとめた確率分布 |
| rbind(y, p0*sum(y)) | # 観測度数とモデルのもとでの期待度数 |
| chisq.test(y, p=p0) | # データが p = 1/3 の二項分布に従っていることの検定 |
| q <- dbinom(x=0:12, size=12, p=pd) | # データから推定された確率に基づく二項分布 |
| q0 <- c(q[1:10], q[11]+q[12]+q[13]) | # 出る回数 10 回以上にまとめた確率分布 |
| rbind(y, q0*sum(y)) | # 観測度数とモデルのもとでの期待度数 |
| r <- chisq.test(y, p=q0) | # データが p = pd の二項分布に従っていることの検定 |
| pchisq(r$statistic, df=r$parameter-1, lower.tail=F) | # 有意確率(自由度1落とす) |
| 女児数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| 度数 | 7 | 45 | 181 | 478 | 829 | 1112 | 1343 |
| 女児数 | 7 | 8 | 9 | 10 | 11 | 12 | 合計 |
| 度数 | 1033 | 670 | 286 | 104 | 24 | 3 | 6155 |
| 虫歯の数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8以上 |
|---|---|---|---|---|---|---|---|---|---|
| 児童の数 | 4 | 9 | 16 | 13 | 9 | 7 | 5 | 4 | 3 |
| y <- c(4,9,16,13,9,7,5,4,3) | # 児童数 |
| n <- 11.3315 | # モーメント法による n の推定値 |
| p <- 0.7729 | # モーメント法による p の推定値 |
| r <- length(y)-2 | # |
| q <- dnbinom(0:r, size=n, prob=p) | # 虫歯数 0 から 7 までの確率 |
| q[r+2] <- pnbinom(r, size=n, prob=p, lower.tail=F) | # 虫歯数 8 以上の確率 |
| rbind(y, q*sum(y)) | # 観測値と期待度数 |
| r <- chisq.test(y, p=q) | # χ2 適合度検定 |
| pchisq(r$statistic, df=r$parameter-2, lower.tail=F) | # 有意確率(自由度 2 落とす) |
課題: 虫歯の数データに,負の二項分布のパラメーターの最尤推定値をあてはめたときの適合度 検定を行い,モーメント法との比較を行え.
| 得点 | 40 未満 | 41 〜 50 | 51 〜 55 | 56 〜 60 | 61 〜 65 | 66 〜 70 | 70 以上 |
|---|---|---|---|---|---|---|---|
| 人数 | 6 | 9 | 12 | 13 | 17 | 14 | 9 |
| 期待度数 | 4.33 | 13.95 | 11.91 | 13.60 | 12.93 | 10.24 | 13.06 |
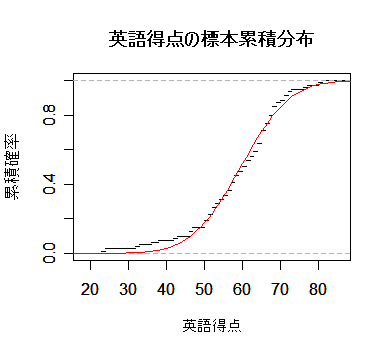
しかしながら,英語得点データのように正規分布などの連続分布をデータにあてはめた場合の あてはまりの良さを調べる場合,χ2 適合度検定は,離散化に恣意性が入るのであまり 薦められない.連続型データの場合は,次に述べる Kolmogorov-Smirnov 検定を用いるのが普通である.

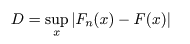
| eigo <- c( 36,70,56,68,76,60,50,63,62,42,64,60,50,68,71,67, | # 英語得点データ |
| 50,65,67,57,72,64,61,66,46,80,46,51,59,32,55,65, 65,52,57,64,23,57,53,54,38,71,57,69,77,61,51,64, | |
| 63,43,65,61,51,69,72,68,53,66,68,58,73,65,62,67, 47,81,47,52,59,33,56,66,67,52,58,65,24,58,54,55) | |
| d <- 5 | # ヒストグラムの階級幅 |
| op <- par(mfrow = c(1, 2)) | # グラフを横に2つ並べて表示 |
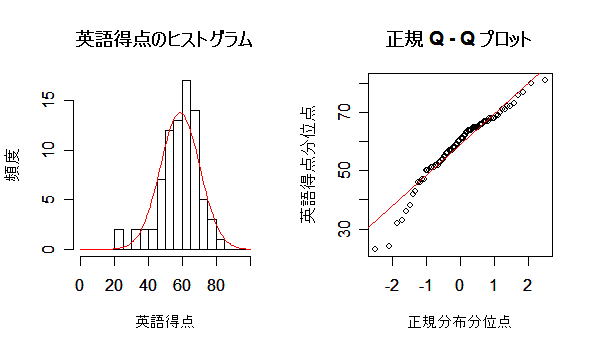
| hist(eigo, breaks=seq(0, 100, by=d), xlab="英語得点", ylab="頻度", main="") | |
| n <- length(eigo) | # データ数 |
| m <- mean(eigo) | # 平均 |
| s <- sd(eigo) | # 標準偏差 |
| x <- 0:100 | # |
| curve(n*d*dnorm(x, m, s), 0, 100, add=TRUE, col="red") | # 推定正規分布重ねて表示 |
| title(main="英語得点のヒストグラム") | # |
| qqnorm(eigo, xlab="正規分布分位点", ylab="英語得点分位点", main="") | |
| qqline(eigo, col=2) | # Q-Q プロット |
| title(main="正規 Q - Q プロット") | # |
| par(op) | # |
| a <- c(0,40,50,55,60,65,70,100) | # 階級の区切り点の定義 |
| b <- hist(eigo, breaks=a) | # 各セルに入る人数の計算 |
| y <- b$counts | # セルの観測度数 |
| l <- length(a) | # |
| p <- pnorm(a[2:(l-1)], mean=m, sd=s) | # 階級の区切りまでの累積確率 |
| ps <- c(0, p) | # |
| pe <- c(p, 1) | # |
| q <- pe-ps | # セルの確率分布 |
| rbind(y, sum(y)*q) | # セルの観測度数と期待度数 |
| r <- chisq.test(y, p=q) | # χ2 適合度検定 |
| pchisq(r$statistic, df=r$parameter-2, lower.tail=F) | # 有意確率(自由度 2 落とす) |
| plot(ecdf(eigo), xlab="英語得点", do.points=F, ylab="累積確率", main="") | |
| curve(pnorm(x, m, s), 0, 100, add=TRUE, col="red") | # 正規分布の累積分布 |
| title(main="英語得点の標本累積分布") | # |
| ks.test(eigo, "pnorm", m, s) | # Kolmogorov-Smirnov 1標本検定 |
課題: 英語得点データでは 25 点以下の 2 名が他の集団から離れているようにみえる. この 2 名を異常値(out-lier)としてデータから除き,正規分布との適合度検定を行い, あてはまりがどう変化したかを考察せよ.