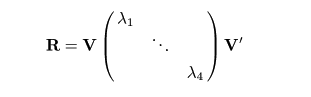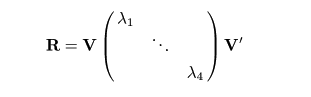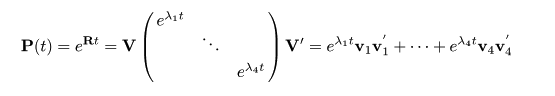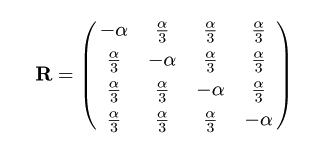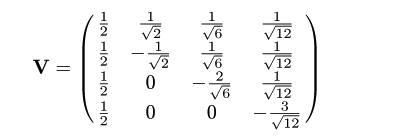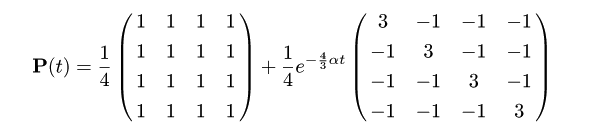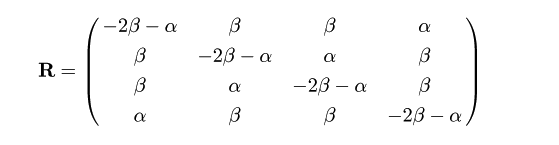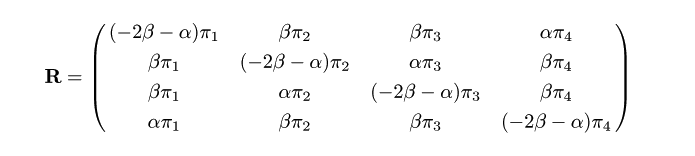2015年度生物測定学応用実験
分子系統樹
東京大学大学院農学生命科学研究科 大森宏
2016年 1月 4日
1. 塩基置換の確率モデル
1-1 データ構造
互いにほぼ相同な m 種の DNA 配列から種の系統関係を推定する
ケースを考える.対象となる種は,
OTU ( Operational Taxonomic Unit ) と呼ばれることも多い.系統関係を推定するための
データ構造は,適切なアラインメントが行われたとすると,
長さ n のサイトからなる 2 次元配列 Xij,
i = 1,…,m,j = 1,…,n,で
表現される.
各サイトの値 Xij は,
塩基配列データならば ATCG のどれかであり,アミノ酸配列であれば 20 種の
アミノ酸のどれかになる.
アラインメント
ある遺伝子に対応する 2 つの
相同なアミノ酸配列や塩基配列を比較するとき,両者のアミノ酸や塩基の数
が異なることがよくある.このとき,欠失や挿入などのギャップを入れて,2 つの
配列をうまく整列させることをアラインメントという.
いま,2つの塩基配列 X,Y を考える.
-
配列 X:ATGCGTCGTT
配列 Y:ATCCGCGAT
この2つの配列は長さが異なるので,1つ以上のギャップ(欠失部位)を入れてアラインメント
させる必要がある.ギャップをできるだけ少なくするのがよいアラインメントである.
これには,色々なアルゴリズムがあるが,直感的にわかりやすいのがドット
マトリックスによる方法である.
- 課題1:上のドットマトリックスを参考にして,配列 X,Y のアラインメントを
行え.
1-2 塩基置換
分子系統樹作成の基礎となる DNA の変化は置換である.これは 1 つのサイトのみ
の変化なので 1 次元の確率モデルを考えればよく,
数学的な取り扱いが比較的容易だからである.また,置換速度などのモデルのパラメータ
の推定も,DNA データからある程度正確に推定できる.塩基置換には次の 2 通りの分類
がある.
トランジションとトランスバージョン
塩基置換には、プリン間 ( A ←→ G ) やピリミジン間 ( C ←→ T ) の
置換である転位 ( トランジション:transition ) と,それ以外の
置換である転換 ( トランスバージョン:transversion ) とがある.一般に,
トランジションの方が起こりやすい.
同義置換と非同義置換
同じアミノ酸をコードするコドン
が複数ある(遺伝暗号の縮退)ので,塩基置換が起こってもアミノ酸が
変化しない場合がある.これを,同義置換 ( synonymous substitution ) といい,
その他の置換を非同義置換 ( nonsynonymous substitution ) という.
コドンの 3 番目(第 3 コドン)は置換しても同義であることが多い.
1-3 置換の数学モデル
塩基配列データについて考えてみる.アミノ酸配列に対する解析もほぼ
同様に行える.
置換推移確率行列
塩基 A, T, C, G の順に 1, 2, 3, 4 と番号づけを行ったとしよう.
時間 t の間に塩基 i か
ら j (i,j = 1, 2, 3, 4) に置換した確率を Pij(t ) と
する.これを並べて,4 × 4 行列
にした P(t ) = (Pij(t )) を置換推移確率行列と呼ぶ.
たとえば,P11(t ) は時刻 0 で A であったサイトが
時刻 t で A であった確率であり,
P12(t ) は時刻 0 で A であったサイトが
時刻 t で T である確率である.
ただし,途中の時刻での塩基は何であってもよい.
P11(t ) は,時刻 0 から t に至る
過程で,A → A という置換が起こらない場合のほか,A → C → A,A → T → G → A など
すべての可能な経路(多重置換)を含んでいる.
マルコフ過程
この塩基置換を連続時間のマルコフ過程 ( Markov process ) と仮定する.これは,あるサイトの
将来の塩基の予測分布は,そのサイトの現在の塩基の状態にのみ依存するとの仮定である.
あるサイトが A という塩基であったとき,将来そのサイトがどの塩基に置換するかは過去のその
サイトの履歴によらないということである.
塩基置換のマルコフ性により
|
Pij(t1 +
t2) =
Σk
Pik(t1)
Pkj(t2),
P(t1 + t2) =
P(t1) P(t2)
|
|
が成り立つ.これを Chapman-Kolmogorov の等式と言う.
置換速度行列
微小時間 Δt においては,置換はあったとしても 1 回しか起こらないとする.
つまり,多重置換は起こらないと仮定する. Δt において
塩基 i から j,(i ≠ j ) の
置換速度 ( substitution rate ) を rijΔt とすると,
置換が起こる確率は,
Pij(Δt )
= rijΔt
であり,置換が起こらない確率は,
Pii(Δt )
= 1 - Σi≠j rijΔt
である.ここで,rii
= -Σi≠j rij とおき,
これを要素にした行列 R = ( rij ) を置換速度行列と定義
する.
この定義より,
Σj rij = 0 であり,
Δt において置換が起きない確率は 1 + riiΔt となる.
置換微分方程式
置換速度行列を用いると,
|
P(t + Δt ) = P(t ) P(Δt ) =
P(t ) + P(t ) R Δt
|
|
となるので,
|
{ P(t + Δt ) - P(t ) } / Δt =
P(t ) R
|
|
すなわち,
という微分方程式を得る.ただし,初期条件は
P(0) = I とする.
いま,R が直交行列 V = (v1
,…,v4) で
対角化され,その固有値がλ1,…,
λ4 であったとする,つまり,
と変形できたとすると,
となる.この置換モデルは特定の塩基が有利になるような選択圧を加えていないので,
過去から現在への時間の経過と現在から過去への時間の遡りが区別できない.
分子進化の中立説の数学的表現である.
1-4 Junks - Cantor (JC) モデル
置換速度行列
塩基置換モデルの最も単純なモデルである.
これは,
置換速度 rij が塩基の組み合わせ
によらず一定値を取ると仮定したもので,他の塩基への置換速度を α とすると,
rij = α/3,(i ≠ j ) としている.
これは,時間 t の間に起こる置換数が平均 αt のポアソン分布に従う
と仮定したモデルである.
置換速度行列は,
となる.R の固有方程式は,
| R - λI | = α(4/3 + α)2 = 0
となるので,
λ1 = 0,
λ2 = λ3
= λ4 = -4α/3
という固有値が得られる.
推移確率行列
固有値に対応する固有ベクトルを並べた直交行列が
となるので,推移確率行列は
となる.
これより JC モデルの基では,t = 0 で A (i = 1) であったサイトが時刻 t で
C (j = 2) となる確率 P12(t ) は,
P12(t )
= (1/4)(1 - e -4αt/3 )
となる.
- 課題2:2 つの OTU X と Y の n サイトを比較したところ,
a サイトが異なっていたとする.塩基置換が JC モデルに従う(式(6)が成立する)とすると,
X と Y の間の JC モデルのもとでの進化距離(サイトあたりの平均置換数)
dXY = αt の推定値を求めよ.
- 課題3:ヒト,ウマ,ウシ,コイのヘモグロビンα鎖
のアミノ酸配列をアラインメントしたところ,140のアミノ酸がほぼ相同で比較可能と考えられた.
4 種のあいだのアミノ酸の違いは,下の表の対角線の上側のようであり,アミノ酸の置換数が
平均αのポアソン分布に従うという置換モデル(JCモデルと同じ)の基での進化距離(サイトあたりの
アミノ酸置換数)の推定値が対角線の下側のように計算された.これを距離行列という.
ヒト・ウマ・ウシは約7,500万年前に分岐したとすると,分子時計が成り立っていると仮定すれば,コイなどの
硬骨魚類とほ乳類は何年前に分岐したと考えられるか.
| | ヒト | ウマ | ウシ | コイ |
| ヒト | | 18 | 17 | 68 |
| ウマ | 0.138 | | 18 | 66 |
| ウシ | 0.129 | 0.138 | | 65 |
| コイ | 0.666 | 0.637 | 0.624 | |
各 OTU 間の進化距離を求めることにより,OTU 間の距離行列が算出される.この距離行列
に基づいて系統樹を作成する手法が平均距離法と近隣結合法であり,後ほど解説する.
1-5 他の置換モデル
Kimura's 2 parameter モデル
塩基にはプリン (A,G) とピリミジン (T,C) の2種類がある.
同種間の置換であるトランジションと異種間の置換である
トランスバージョンに分けて考えると,トランジションの方が起こりやすいことが
知られている.そこで,
トランジションの置換速度を α,トランスバージョンの置換速度を β と
おくと,速度行列 R は,
となる.推移確率行列は前節と同様にして計算できる.
HKY ( Hasegwa, Kishino, Yano ) 85 モデル
トランジション,トランスバージョンの違いのほか,塩基組成の違いを考慮にいれた
モデルである.A,T,C,G,の塩基組成頻度をそれぞれ,π1,
π2,
π3,π4,とすると,
速度行列は,
となる.
2. 系統樹作成手法
系統樹
系統樹の分岐パターンを樹形(topology)と言う.通常,遺伝子や生物種の系統関係
は,祖先種から現存種への進化の道筋を示す根をもった樹状図で示される.
これを有根系統樹(rooted tree)と言う.根が共通祖先で,末端が現存種である.
根,末端,分岐点を総称してノード(node)という.
一方,根のない系統樹を描くこともできる.これは、OTU 間を 2 分岐型
で結んだもので,無根系統樹(unrooted tree)あるいはネットワーク(network)
と呼ばれている.
系統樹のもつ情報としては,分岐パターンを表す樹形の他,進化距離を表す枝長がある.
枝長が長いほど塩基置換数が多く,それだけ遺伝情報が変化したことを表す.また,分岐
の信頼性の指標として,分岐点のブーツストラップ頻度を記入することもある.
2-1 OTU 間の進化距離行列に基づく手法
平均距離法(UPGMA)
結合した OTU 間の距離を,もともとの距離の算術平均を用いて再定義する手法で
UPGMA ( Unweighted Pair Group Method with Arithmetic Means ) と呼ばれる.
この手法は類似度関係図を作成するために開発されたが,距離の期待値が進化時間に
近似的に比例する場合は,系統樹作成に使える.
いま,4 OTU に対して,OTU i と j の間のなんらかの
進化距離 ( dij )
が計算され,以下の距離行列を得たとする.
| OTU | 1 | 2 | 3 |
| 2 | d12 | | |
| 3 | d13 |
d23 | |
| 4 | d14 |
d24 |
d34 |
この距離行列の中で,d34 が最小だったとする.
すると,OTU 3 と OTU 4 が d34/2 の距離の分岐点で結合され,
合体した OTU(34) が作られる.合体した OTU と他の OTU との間の距離は,例えば,
OTU 1 と OTU(34) では d1(34) =
( d13 + d14 )/2 のように計算する.
この結合の結果,新しい距離行列,
| OTU | 1 | 2 |
| 2 | d12 | |
| (34) | d1(34) |
d2(34) |
が得られる.この距離の中で最小の距離をもつ OTU を結合する.こうして,
すべての OTU が結合して 1 つの OTU になるまで続ける.その結果,有根系統樹が生成される.
近隣結合法(Neighbor-Joining; NJ)
OTU 間の進化距離行列から枝長の総和を最小にする無根系統樹を作る手法である.
NJ法のアルゴリズムは以下のようにまとめられる.
- ノード i に対して他のノードからの距離の総和,
ri
= Σk=1, N dik
を計算する.ただし,dik はノード間の距離で,N は現在の距離行列
におけるノードの数である.
- 以下の値 Mij を最小にするペアー i, j を見つける.
Mij = dij -
(ri + rj )/(N - 2)
- 見つけたペアー i, j を結合して新しいノード u をつくる.
ノード i, j と u との間の枝長は,
siu = dij /2 +
(ri - rj )/{2(N - 2)},
sju = dij
- siu
と算出し,u から他のノード k からの距離は,
dku =
( dik
+ djk - dij )/2
と計算する.
- ノード i, j を全体の距離行列から取り除き,N を1つ減らす.
- 2 つ以上のノードが残っているときは1にもどる.
- 課題4:ある遺伝子の DNA データを用いて,
ヒト(H),チンパンジー(C),ゴリラ(G),オラウータン(O)の間の進化距離を
推定したところ以下のようなデータがえられた.
| OTU | H | C | G |
| C | 0.0931 | | |
| G | 0.1095 | 0.1135 | |
| O | 0.1802 | 0.1942 |
0.1882 |
この距離行列から UPGMA 法と NJ 法それぞれで,枝長を明示した系統樹を
上記のアルゴリズムを参考にして手計算でつくれ.
2-1 OTU の塩基データから直接生成する手法
節約法(Parsimony methods)
与えられた OTU に対してある特定の樹形を仮定し,この樹形のもとでの
祖先種のアミノ酸もしくは塩基配列をなるべく置換が少ないようにして推定する.
そして,配列の進化的変化を説明するのに必要な置換数の最小値を数える.
次に,別の樹形を考えその最小置換数を数える.こうして,合理的と考えられる
可能なすべての樹形について調べ上げ,最小の置換数を
与える系統樹を選び出す.この方法で得られた系統樹を
最大節約(maximum parsimony)系統樹と呼ぶ.
節約法はおもに樹形の決定に用いられ,枝長の推定はできない.
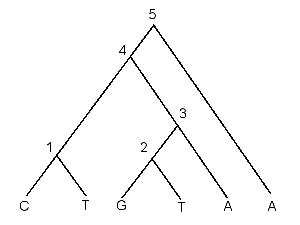
- 課題5: 6 つの OTU の系統樹を下の図のように仮定した.これらの OTU のある
サイトにおける塩基が下段のようであったとする.塩基置換をなるべく少なく
したときの最小置換数はいくつか,またこのとき,ノード 4
とノード 5 の塩基はどのようなものであったと推定されるか.
最尤法
特定の置換モデルを仮定して,
多くの樹形で OTU データで観察された塩基配列を得る尤度(確率に比例した量)を
計算し,その中で最大の尤度をもつ樹形を選ぶ.樹形と枝長の両方が同時に求められる.
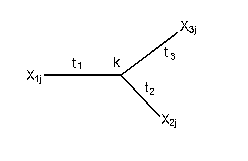
簡単のため,3 つの OTU の場合を考える.これらの第 j サイトの塩基をそれぞれ
X1j,
X2j,
X3j,とする.
3OTU からなる無根系統樹は下の図のようになる.中心のノードからの進化時間(枝長)を
それぞれ t1,
t2,
t3,と
おく.塩基置換モデルのパラメータを θ とする.JC モデルのもとでは,θ = α で
あり,Kimura's 2 parameter モデルのもとでは θ = (α,β)である.また,塩基組成頻度(事前確率)を
πk とする.通常は,
πk = 1/4 である.
中心のノード k の塩基は未知であり,k = 1, 2, 3, 4(A,T,C,G)の
いずれかであるので,想定した塩基モデルのもとで上の図のような系統樹が生じる
尤度(確率)は,式(4)の推移確率行列を用いて,
Σk πk
PX1j
k(t1 )
Pk X2j(t2 )
Pk X3j(t3 )
と計算される.他のサイトの置換は互いに独立であると仮定すると,
n サイトからなる 2 次元配列 Xij が生成する尤度は,
|
L( Xij | θ,
t1,t2,
t3 ) = Πj
Σk πk
PX1j k(t1 )
Pk X2j(t2 )
Pk X3j(t3 )
|
となる.この値を最大にするようなパラメータ θ と枝長 t1,
t2,
t3 を求める.
OTU の数が増加すると可能な系統樹の樹形(topology)も増加する.原理的には可能なすべての
樹形に対して尤度が最大となるパラメータと枝長を求め,その中で尤度が最大となる樹形を選ぶ.
一般に,可能なすべての樹形をしらみつぶしに調べることは不可能なので,
探索アルゴリズムを用いて近似的に最大尤度の樹形をみつける.このようにして,配列データ
を生成する確率が最大となる系統樹が得られる.
参考文献
分子進化遺伝学,根井正利,(Molecular Evolutionary Genetics, 五條堀孝・斎籐成也 共訳,根井正利 監訳),
培風館,1990.
Copyright (C) 2004, Hiroshi Omori. 最終更新:2008年10月 2日