対象間の類似関係もしくは非類似関係が与えられると， 多次元尺度法(MDS: Multi-Dimensional Scaling)により対象全体の 構造が視覚化できる．これは， 類似した対象どうしを近く，類似していない対象どうしを遠くに配置させることにより， 対象の布置を求める手法である．
　MDS には計量的(metric)MDS と非計量的(non-metric)MDS とがある．計量的MDS は対象間の 非類似関係が，対象間距離と比例していると考えられるときに用いられる． しかし，非類似関係は色々な方法で推定されるので，距離と比例関係にあることは あまりないと思われる．このようなときに計量的MDS を適用すると布置に歪みが生じる 場合がある．このため非類似度の数値ではなく大小関係のみを用いた非計量的MDS が実際の データではよく適用される．
　多次元尺度法は，なるべく小さな次元でストレスが小さな(0.1程度)布置をみつけ て対象間の距離情報を視覚化しようとしたものである．

多次元尺度法(MDS)

• 中心化
  n 個の対象に対する p 次元の n×p 座標 行列を X = (x_ij) とする．さて， X^* = (I-11'/n)X という演算を中心化という． ただし，I は単位行列，A' は A の転置行列， 1 = (1,…,1)' である．
  対象全体での平均座標を m₁,…,m_p， m_j = ��x_ij/n と すると，中心化を行った行列 X^* の要素は， x^*_ij = x_ij - m_j となるので，その列和は 0 となる． なお，(I-11'/n) を中心化行列という．
  　
• ヤング・ハウスホルダー(Young-Householder)変換
  n 個の対象に対する p 次元の n×p 座標行列を X とする． この座標から生成される n×n 距離行列を D，距離の2乗の 行列を D⁽²⁾ とする．D⁽²⁾ は，
  
  となる．ただし， diag(A) は対称行列 A の対角成分だけを 抜き出した対角行列である．
  距離の2乗の行列に両側から中心化行列をかける演算をヤング・ハウスホルダー変換と いう．(I-11'/n)1 = 0， 1'(I-11'/n)=0 に注意すると，
  
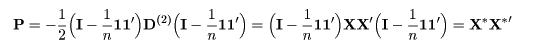
  となる．これより，中心化された座標行列 X^* は，距離の2乗の 行列 D⁽²⁾ にヤング・ハウスホルダー変換を行った行列 P を スペクトル分解 することにより得られることがわかる．
  　
• 計量的MDS
  n 個の対象間の距離の2乗とみなせる非類似度行列 S が得られたとする． S にヤング・ハウスホルダー変換を施した行列 P を直交 行列 T でスペクトル分解すると，
  
  となる．対角行列 Λ の正固有値は高々 n-1 個である．ここで， Λ の大きな固有値から r 個の要素を取り出し，他を0とした対角行列 を Λ_r，取り出された固有値に対応する固有ベクトルを並べた行列 を T_r とし， X_r=T_rΛ_r^1/2 と おくと，
  
  は，P を
  
  の意味で最小化（最小2乗法）したことになる． この X_r を r 次元における対象の布置 としたものが計量的MDSによる解である．対象間距離の2乗のうち， r 次元布置 X_r で表現される距離の2乗の割合は， 取り出した r 個の固有値の累積寄与率で測ることができる． この手法は， 主座標分析(principal coordinate analysis)とも呼ばれることもある．
  　
• 非計量的MDS
  対象間の非類似性値そのものではなく，非類似性の順序情報のみを 用いて対象の空間布置を求める手法である．よく用いられるのは，Kruskal の方法 (Kruscal, 1964)である．
  対象間の非類似度行列 S = (s_ij) の要素に対する任意の単調 変換を δ_ij=h(s_ij) とする．r 次元での対象 の布置 X_r から得られる距離行列を D_r = (d(r)_ij) とする．非計量的MDSは，
  
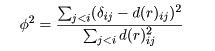
  を最小にする δ_ij と X_r を同時に探索する 手法である．φ はストレスと呼ばれ，これが 0.1 以下になるのがよいとされている．