統計言語「
R」では,他のユーザーの作成したパッケージを利用することにより,新規性や特異性が高く普通の統計ソフトでは解析できないような手法も用いることができます.ここでは,一例として,楕円フーリエ記述子に基づく輪郭形状の統計解析手法について簡単に説明します.【
A-1】楕円フーリエ記述子に基づく輪郭形状の定量的評価輪郭形状の定量的評価法のひとつに楕円フーリエ記述子(
elliptic Fourier descriptors: Kuhl and Giardina 1982)とよばれる手法があります.この手法は,輪郭の座標情報を周期関数として表し,そのフーリエ級数の係数によって形を記述します.具体的には,輪郭上のある点Sから出発し,輪郭上を一定の速度で周回する点Pを考えます.ここで,点Pの時刻tにおけるx,y座標をそれぞれx(t), y(t)と表すと,点Pは輪郭上を1周するごとに出発点Sに戻ってくるため,x(t), y(t)は周回時間Tを周期とする周期関数となります.周期をもつ関数はフーリエ級数により記述できるので,x(t), y(t)は以下のように表すことができます.![]() (1)
(1)
![]() (2)
(2)
すなわち、フーリエ級数の係数
an, bn, cn, dnによって輪郭の座標情報を記述することができます.ただし,これらフーリエ係数は,輪郭の向きや大きさ,さらには出発点の位置により値が変化します.そこで,係数について輪郭の向きや大きさ,出発点の位置に対する標準化を行い,標準化された係数を形の記述子として用います.楕円フーリエ記述子に関する詳細については,KuhlとGiardina (1982),RohlfとArchie (1984),岩田(2000),岩田(印刷中)などを参考にして下さい. 【A-2】輪郭形状の統計解析楕円フーリエ記述子ではフーリエ係数で座標情報を記述しますが,係数の数は式
(1), (2)のNが20のときに80個となります.しかし,このままでは係数の数が多すぎて形の変異を簡単に解釈できません.そこで,主成分分析という多変量解析の手法を用いて,係数に含まれている情報をより低い次元の情報に縮約します。具体的には,係数の分散共分散行列に基づく主成分分析を行い,その主成分得点を形の評価値として用います.なお,フーリエ係数に含まれている情報は必ずしも主成分分析で評価しなければならないわけではありません.クラスタ解析や正準判別分析など他の多変量解析手法によって,主成分分析では評価できなかった特徴を評価できることもあります. 楕円フーリエ記述子の利点のひとつとして,係数の値から逆に輪郭を構築できることが挙げられます.この性質を利用することにより,主成分として抽出された形の特徴を視覚的に表現することができます(Rohlf and Archie 1984).これにより,通常の主成分分析では難しい各主成分の意味の解釈が容易になります.【
A-3】Rを用いた輪郭形状の統計解析楕円フーリエ記述子を用いた輪郭形状解析のためのソフトウェアとして,「
SHAPE」(Iwata and Ukai 2002)というフリーウェアがあります(http://cse.naro.affrc.go.jp/iwatah/shape/index.htmlよりダウンロード可能).SHAPEは、Windows上で動作し,(1) 画像解析による輪郭抽出,(2) 楕円フーリエ記述子の導出と標準化,(3) 主成分分析,(4) 主成分の意味の視覚化といった,一連の操作を実行できます.SHAPEを用いれば,画像解析や統計解析にあまり心得のない人でも,容易に解析をすすめることができます.しかし一方で,手法の一部を改変して解析したい場合には,SHAPEはあまり融通がききません.そこで,本稿の著者の一人である岩田は, SHAPEで実行される操作のうち,画像解析を除いた全ての操作をR上で行うためのパッケージ「SHAPE on R」を作成しました.ここでは,そのSHAPE on Rについて簡単に紹介します.shape.r SHAPE on R
本体(Rの関数群)sample_chc.dat
サンプルデータ(チェーンコードとして保存された輪郭)sample_nef.dat
サンプルデータ(楕円フーリエ記述子)chc2r.pl SHAPE
からSHAPE on Rへのデータコンバータ,Perl
プログラム,チェーンコード用.nef2r.pl
同上,楕円フーリエ記述子用.sample_chc.chc SHAPE
用サンプルデータ(チェーンコード)sample_nef.nef SHAPE
用サンプルデータ(楕円フーリエ記述子)# SHAPE on R
> source("shape.r")
#
サンプルデータの読み込み.データはread.tableではなく専用の関数read.chcで読み込む.> sample.chc <- read.chc("sample_chc.dat")
Read 138 records
#
チェーンコード(Freeman 1974)として保存されている輪郭情報を標準化楕円フーリエ記述子に変換する.変換されたデータはsample.nefという名前のデータセットとして保持される.> sample.nef <- chc2nef.chcdata(sample.chc)
1:next
2:back
3:turn
4:end
Selection:
#
メニューから番号で操作を選択する.変換された記述子から再構築された輪郭が表示される.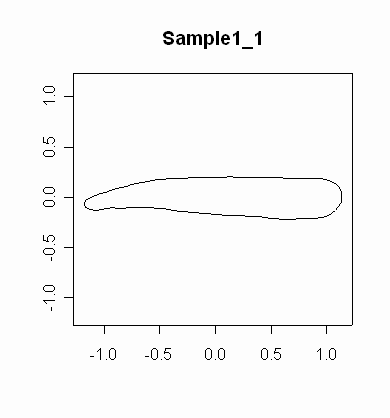
#
標準化楕円フーリエ記述子から輪郭を構築する.> draw.efdata(sample.nef)
1:next
2:back
3:end
Selection:
#
メニューから番号で選択.#
標準化楕円フーリエ記述子の主成分分析を行う.> pca.res <- pca.efdata(sample.nef)
#
主成分分析結果を確認する#
固有値> pca.res$eval
PC 1 PC 2 PC 3 PC 4 PC 5 PC 6
1.071930e-03 3.371277e-04 1.462083e-04 7.946575e-05 ...
(略)#
寄与率> pca.res$contr
PC 1 PC 2 PC 3 PC 4 PC 5 PC 6
5.727006e+01 1.801175e+01 7.811479e+00 4.245622e+00 ...
(略)#
累積寄与率> pca.res$cum.contr
PC 1 PC 2 PC 3 PC 4 PC 5 PC 6 PC 7 PC 8
57.27006 75.28181 83.09329 87.33891 90.63505 ...
(略)#
第1〜4主成分得点を表示する.> pca.res$score[,1:4]
PC 1 PC 2 PC 3 PC 4
Sample1_1 2.689132e-02 -0.0304498884 -1.861971e-02 -0.0006565109
Sample1_2 1.146167e-02 -0.0155943836 -1.308370e-03 0.0121484834
(略)
#
第1〜4主成分得点のタブ区切りテキストファイルとして保存する.>write.table(pca.res$score[,1:4],file="score.dat",quote=F,sep="\t")
#
主成分の意味を視覚化する.> draw.pc(pca.res)
1:next
2:back
3:minus
4:mean
5:plus
6:end
Selection:
#
メニューから番号で選択する.各主成分の評価する形の特徴が表示される.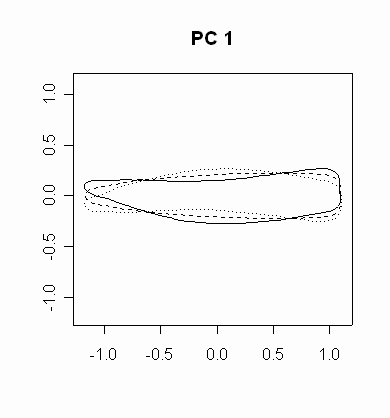
chc2r.pl
およびnef2r.plは,以下のように用いればSHAPE用ファイルからSHAPE on R用ファイルに変換できます.【
A-5】参考文献Freeman, H. (1974) Computer processing of line drawing images. Comp. Surv. 6: 57-97.
岩田洋佳(
2000)植物の形をはかる −植物形態の定量的評価ならびに統計遺伝学的解析−. 育種学最近の進歩 第42集. 57 - 60.岩田洋佳(印刷中)楕円フーリエ記述子に基づく植物形態の統計遺伝学的研究
. 日本計量生物学会誌.Iwata, H. and Y. Ukai (2002) SHAPE: A computer program package for quantitative evaluation of biological shapes based on elliptic Fourier descriptors. Journal of Heredity 93: 384-385.
Kuhl, F. P. and C. R. Giardina (1982) Elliptic Fourier features of a closed contour. Comp. Graph. Image Process. 18: 236-258.
Rohlf, F. J. and J. W. Archie (1984) A comparison of Fourier methods for the description of wing shape in mosquitos (Diptera: Culicidae). Syst. Zool. 33: 302-317.