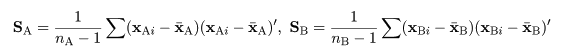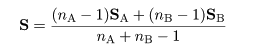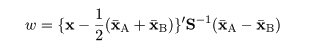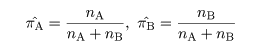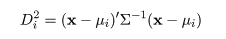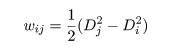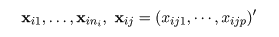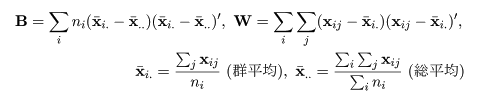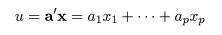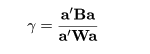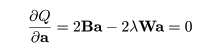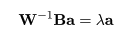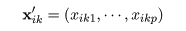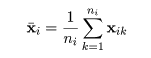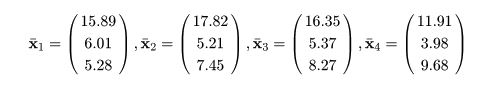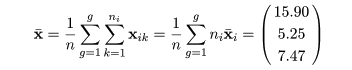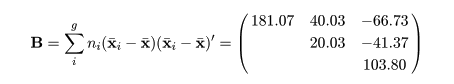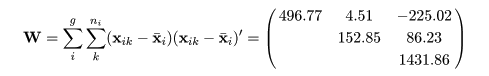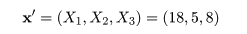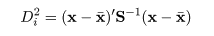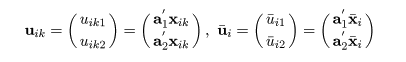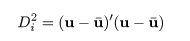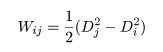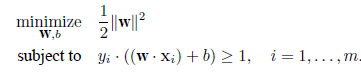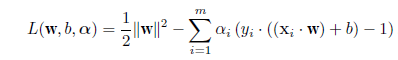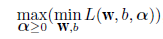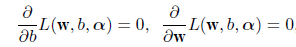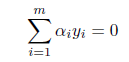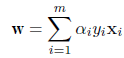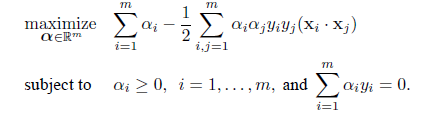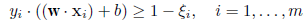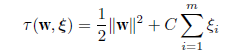数理統計学演習
判別分析
東京大学大学院農学生命科学研究科 大森宏
判別分析とは
2.2群の判別
2−1.空間の分割と判別規則
母集団が2つの部分母集団 A,B の混合からなっている場合を考える.
部分母集団 A,B の確率密度をそれぞれ
fA(x ),fB(x )
とし,その混合比率をπA,πB とすると,母集団全体の確率密度は,
f (x ) = πAfA(x )
+ πBfB(x )
(1)
となる.いま,帰属未知の対象 X の属性値 x に基づき部分母集団への帰属を決めるとする.このとき,
x の取り得る値の全体(標本空間) R は,RA と RB に分割され,
x ∈ RA なら X は A に帰属,
x ∈ RB なら X は B に帰属.
となる.これを判別規則という.
2−2.最適な判別規則
x の空間 R の分割が判別規則に対応するが,どのような空間分割を行うのがよいであろうか.
まず,ベイズの定理による事後確率の最大化という考え方がある.
ベイズ(Bayes)の定理
P(A) を事象 A が起こる確率,P(A|B) を事象 B が生起したもとでの事象 A が起こる条件付き確率,
P(A∩B) を事象 A と事象 B が同時に生起する確率とすると,
P(A∩B) = P(A|B)P(B) = P(B|A)P(A)
が成り立つので
P(A|B) = P(B|A)P(A)/P(B)
である.これをベイズの定理と言う.
いま,標本空間 Ω が互いに排反な事象,
A1,…,An
(P(Ai∩Aj,i≠j,
P(A1∪…∪An) = P(A1)+…+P(An)=1),
に分割されたとすると,Ω の任意の部分集合 B の生起する確率 P(B) は,
P(B) = P(B|A1)P(A1)+…+P(B|An)P(An)
= ΣiP(B|Ai)P(Ai)
と表現される.これより,事象 B が生起したときの事象 Ai が生起する事後確率は,
と表せる.
ベイズ判別規則
対象 X が A に帰属したとき,対象 X の値が x のごく近傍を取る確率は,
P(x |A) = fA(x )Δx であり,対象 X が B に帰属したとき,
x のごく近傍を取る確率
は,P(x |B) = fB(x )Δx とあらわせる.
対象 X の値が x の近傍であるとき,X が部分母集団 A 由来である事後確率は,
P(A) = πA に注意すると,
であり,X が部分母集団 B 由来である事後確率は,
となる.事後確率の高い部分集団に対象 X を帰属させるとすると,
対象 X は A 由来と判定 ⇔ P(A|x ) > P(B|x ) ⇔
πAfA(x ) > πBfB(x )
⇔ logπA + logfA(x ) >
logπB + logfB(x ),
すなわち,
RA = { x | logπA + logfA(x ) >
logπB + logfB(x ) }
(2)
となる.
誤判別確率最小判別
判別規則により,対象 X を判別したとする.このときは次のような誤判別がある.
- X は A から得られたのに B から得られたと判別する.この確率を Pr[B|A] とおく.
- 逆に,X は B から得られたのに A から得られたと判別する.この確率を Pr[A|B] とおく.
すると,誤判別の確率は,
となる.これより,RA として,
の部分のみを含み,
の部分をふくまなければ誤判別確率は最小となる.よって,式(2)と同じ判別規則が得られる.
1次元分布での判別
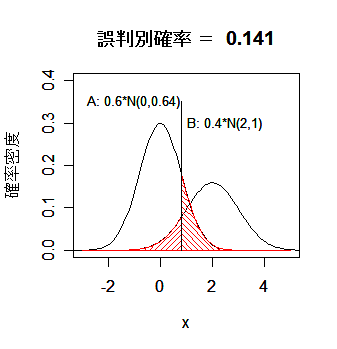
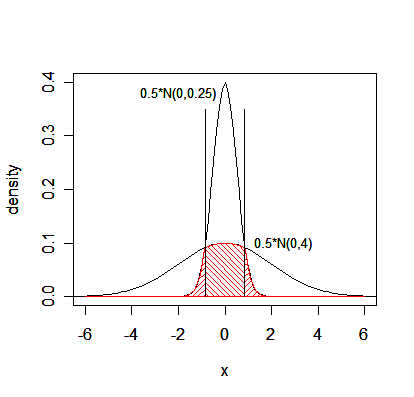
母集団が1次元の分布の場合の判別による空間(数直線)分割の例を以下に示す.
 |
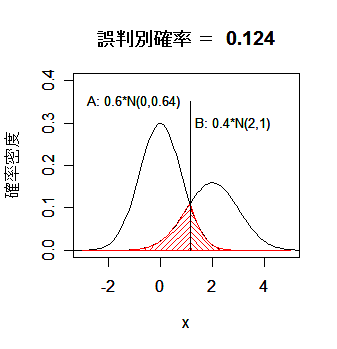 |
図1.空間の分割と誤判別確率
図2.分散のみが異なるときの空間の分割
 |
2−3.線形判別関数
正規母集団のもとでの判別規則
部分母集団が正規分布で記述されているときは,簡単な判別規則をつくることができる.
平均 μ,分散共分散行列 Σ の p 次元正規分布の密度関数は,
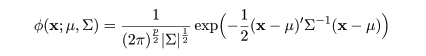
|
(3)
|
と表せ,その対数は,
とかける.部分母集団 A,B の平均を μA,μB,分散共分散行列を
ΣA,ΣB とすると,対象 X は A 由来と判定する領域は,
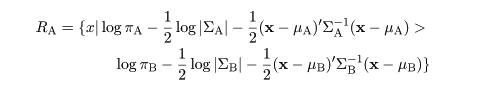
|
(4)
|
と表せる.ここで,部分母集団 A,B が共通の共分散行列 Σ をもち,その存在比率が等しい
(πA = πB = 1/2)とすると,A 由来と判定する領域は,
と簡略化される.
マハラノビス距離
ところで DA,
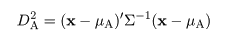
|
(5)
|
を,部分母集団 A と対象の値 x とのマハラノビス(Mahalanobis)距離という.この距離は,通常
のユークリッド(Euclidean)距離と異なり,分布を考慮にいれた距離で,マハラノビス距離が小さい方の部分
母集団の方が x の近傍のような値が得られる確率が高い(起こりやすい)ことを意味
している.つまり,マハラノビス距離の近い部分母集団に対象を割り付ける,という判別規則となる.
線形判別関数の導出
部分母集団 A,B と対象の値 x とのマハラノビス距離,
DA,DB,を用いると,
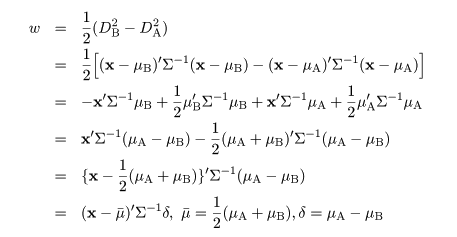
|
(6)
|
という x の線形関数ができる.これを線形判別関数(linear discriminant function)という.
判別規則は,
w > 0 ⇔ 対象 X は A 由来と判定,w < 0 ⇔ 対象 X は B 由来と判定,
となる.つまり,超平面 w = 0 により,標本空間が2つに分割される.
線形判別関数の例
2変量正規母集団を考える.部分母集団 A,B の平均 μA,μB と共通の
分散共分散行列 Σ が,
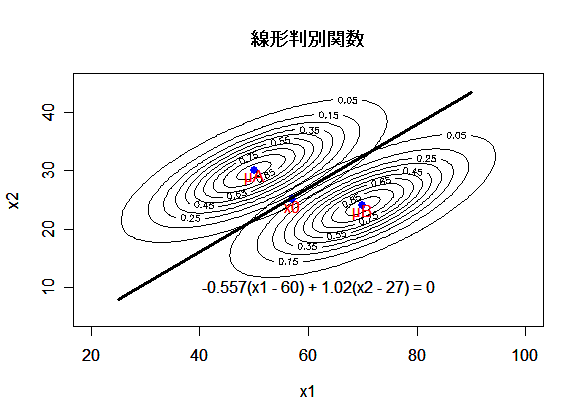
であったとする.このとき,部分母集団 A,B が定義されている平面を分割する線形判別関数は,
と計算できる.
図3.2つの2次元正規母集団に対する線形判別関数
 |
母集団比率を考えた線形判別関数
母集団構成比率 πA,πB が既知であるときや,未知でもこの
比率に大きな偏りが認められる時は構成比率の値を考慮に入れた判別関数をつくるべきである.
式(4)の判別領域で,log|ΣA|,log|ΣB| の項を消去すると,対象 X を A 由来
と判別する領域は,
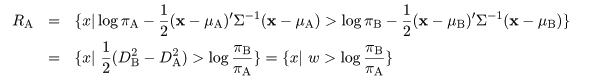
(7)
となる.
母集団母数が未知の場合
部分母集団 A,B の母数が未知であるのが普通である.このときは部分母集団への帰属がわかっている
トレイニングデータ(training data),教師データともいう,から母集団母数を推定する.
部分母集団 A,B それぞれから大きさ nA,nB のトレイニングデータが得られた
とすると,それぞれの標本平均,
で母集団平均 μA,μB が推定される.
部分母集団 A,B の分散共分散はそれぞれの群内標本分散共分散行列,
で推定されるが,両者が等しいと考えられるときは,共通の分散共分散行列が重みづけ平均,
で推定される.これを用いて,分類未知の対象 x に対する線形判別関数が,
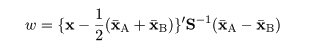
|
(8)
|
と推定できる.また,部分母集団の構成比率は,トレイニングデータが完全にランダムに抽出された
とすれば
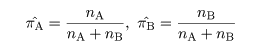
|
(9)
|
で推定できる.
3.多群の判別
4-1.一般規則
母集団が g 個の部分母集団にわかれていて,各部分母集団の構成比率が πi で,その
密度関数が fi(x ) であるとすると,母集団全体の確率密度は,
f (x ) = π1f1(x ) +…+
πgfg(x )
(10)
と表せる.2群の判別のときと同様に考えると,帰属未知の対象 X の値 x が得られたとき
対象 X は群 i 由来と判定 ⇔
πifi(x ) が最大
という判別規則となり,x の取り得る値の全体空間が g 個に分割される.
4-2.分散共分散が等しい正規群集団
部分母集団が正規分布であり,分散共分散行列 Σ が共通で,平均が互いに異なる μi であり,構成
比率も等しいときは,対象 X から部分母集団平均までののマハラノビス距離,
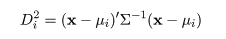
|
(11)
|
が最小となる群 i に割り付ける.また,gC2 個の線形判別関数を式(6)により,
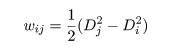
|
(12)
|
のように作成し,wij > 0 が成り立てばグループ i に対象を帰属させる方式
を順々に行えば,最も適当な帰属先が求まる.
4.正準判別
母集団分布が多変量のとき,判別のようすを視覚化することは難しい.そこで,主成分分析と似たような考え方
で次元を縮約して,判別を比較的少数の次元で行う手法がある.これが正準判別である.
いま,p 次元空間に g 個の部分母集団があり,i 番目の部分母集団から大きさ ni の
トレイニングデータ,
が得られたとする.トレイニングデータ全体での偏差積和行列 T は,データの各群への割付により,
群間偏差積和行列 B と群内偏差積和行列 W に,
T = B + W
(13)
のように分解される.なお,
である.ここで,分類未知の対象 X の値 x が与えられたとする.
このとき,x の線形結合,
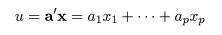
|
(14)
|
を考える.
x の分散が Var[x] = Σ のとき,u の分散は,
Var[u } = Var[a'x] =
a'Σa
となることから,トレイニングデータ全体での u の総平方和は a'Ta と
あらわされ,これが
a'Ta
= a'Ba + aWa
(15)
のように分解される.a'Ba は u の群間平方和で,
a'Wa は u の群内平方和である.
判別に有効と考えられる線形結合 u は,群の差をなるべく大きくするのがよいので,群間と群内の比
がなるべく大きくなる係数 a を求めればよい.
一意的な a を求めるため,a'Wa = 1 と基準化すれば,
a はラグランジュの未定係数法を用いて,
Q = a'Ba − λ (a'Wa − 1 )
を最大化すればよい.Q を a で偏微分して 0 とおくと,
となるので,
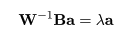
|
(16)
|
という方程式が得られる.これより,a は W-1B の固有
ベクトルであることがわかる.固有値 λ は,λ = a'Ba
となり,線形結合 u の群間平方和となっている.
W-1B の階数 m は,m ≦ min(p, g−1) であり,全部で m 個の正の固有値
が得られ,残りは 0 固有値となる.正の固有値を大きい順に並べて,
λ1 ≧ λ2 ≧ … ≧ λm
とおく.個々の固有値 λi に対応する固有ベクトル ai により,
線形結合 ui = ai'x が得られる.
u1 が最もよく群間の変動を説明し,u2 がその次に群間の変動を説明する,
というようになる.この ui を正準変量と呼ぶこともある.
通常は,u1,u2 で群間の変動のかなりの部分が説明されるので,データを
この2つの正順得点で (u1,u2 ) 平面上にプロットし,判別関数で平面
を分割すれば,判別の様子が視覚化される.
また,i≠j のとき,ai'Waj = 0,が成り立つ
ので,u1 と u2 は群内で無相関となる.しかし,
ai'aj ≠ 0 なので,ui 軸と
uj 軸は直交しない.この点が主成分分析による次元の減少とは異なっている.
5.多群の判別の実例
文献[2]による.肥満の程度で4つの群に分類された若い男性の尿標本の生化学特性データが表1にある.
これは,クレアチン色素(X1),塩化物(X2),
コリン(X3)の測定データからなっている.これが,トレイニングデータとなる.
データダウンロード
5-1.全情報利用による判別
データの群平均と総平均の計算
データにおける変数の数を p,群の数を g として,i 番目の群における k 番目の標本(個体)の r 番目の
観測値を xikr,k = 1,…,ni,とおく.総標本数を
n = n1 + … + ng とする.表1の例では,p = 3,g = 4,
n = 12+14+11+8 = 45,である.
各群における標本ごとの観測値ベクトルを,
とおき,標本平均ベクトルを
とおく.表1の例では,
となった.また,総平均ベクトルは
となった.
いま,表1のデータが R の作業フォルダに "nyo.csv" という名前で保存されているとする.
これらの計算を R で行うスクリプトを以下に示す.
- nyo.dfr <- read.csv("nyo.csv")
- nyo.dfr
- n1.m <- nyo.dfr[1:12,2:4] #data matrix of group1
- n2.m <- nyo.dfr[13:26,2:4]
- n3.m <- nyo.dfr[27:37,2:4]
- n4.m <- nyo.dfr[38:45,2:4]
- g1.m <- mean(n1.m) #mean of group1
- g2.m <- mean(n2.m)
- g3.m <- mean(n3.m)
- g4.m <- mean(n4.m)
- t.m <- mean(nyo.dfr[,2:4]) #total mean
群内平方和積和行列と群間平方和積和行列
表1データの群間平方和積和行列 B と群内平方和積和行列 W は,
と計算された.R のスクリプトを以下に示す.
- w1 <- var(n1.m)*(nrow(n1.m)-1)
- w2 <- var(n2.m)*(nrow(n2.m)-1)
- w3 <- var(n3.m)*(nrow(n3.m)-1)
- w4 <- var(n4.m)*(nrow(n4.m)-1)
- w.mat <- w1 + w2 + w3 + w4 #matrix of within sum of squares
- b1 <- (g1.m-t.m) %*% t(g1.m-t.m) * nrow(n1.m)
- b2 <- (g2.m-t.m) %*% t(g2.m-t.m) * nrow(n2.m)
- b3 <- (g3.m-t.m) %*% t(g3.m-t.m) * nrow(n3.m)
- b4 <- (g4.m-t.m) %*% t(g4.m-t.m) * nrow(n4.m)
- b.mat <- b1 + b2 + b3 + b4 #matrix of between sum of squares
対象と群平均とのマハラノビス距離
各群平均 μi の最尤推定値は標本平均ベクトル xi であり,各群
共通の分散共分散行列 Σ の不偏推定値行列は,S = S/(n−g) と推定される.
いま,未分類の対象データ
が与えられたとする.対象 x と群平均とのマハラノビス距離の推定値を
で計算すると,
D12 = 1.2386,D22 = 0.0334,
D32 = 0.2820,D42 = 3.3164
が得られた.これより,D22 が最も小さいので, x はグループ2
に判別された.R のスクリプトを以下に示す.
- s.mat <- w.mat/41 #sample covariance matrix
- x <- c(18,5,8) #unknown sample to discriminate
- mahalanobis(x, g1.m, s.mat) #mahalanobis distance between x and group1 mean
- mahalanobis(x, g2.m, s.mat)
- mahalanobis(x, g3.m, s.mat)
- mahalanobis(x, g4.m, s.mat)
線形判別関数の利用
群の数が 4 なので,4C2 = 6 通りの線形判別関数を式(12)に基づいてつくることが
できる.群 i と群 j を判別する判別関数を wij とすると,
| w12 = |
-0.2130X1 + 0.2841X2 − 0.1129X3 + 2.7134 |
| w13 = |
-0.0915X1 + 0.2390X2 − 0.1146X3 + 0.8915 |
| w14 = |
0.2685X1 + 0.6048X2 − 0.1202X3 − 5.8555 |
| w23 = |
0.1214X1 − 0.0451X2 − 0.0018X3 − 1.8219 |
| w24 = |
0.4814X1 + 0.3207X2 − 0.0074X3 − 8.5689 |
| w34 = |
0.3600X1 + 0.3658X2 − 0.0056X3 − 6.7470 |
となる.ここで,wij = -wji,
w23 = w13 − w12,のような
関係が成立していることに注意せよ.
対象 x が与えられたときに,グループ1由来であると判別されるのは,
w12 > 0,w13 > 0,w14 > 0
の場合である.x = (18,5,8)' という対象に対しては,
w12 = -0.6026,w13 = -0.4783,w14 = 1.0389,
w23 = 0.1243,w24 = 1.6415,w34 = 1.5172,
となった.これより,
w21 = -w12 > 0,w23 > 0,w24 > 0
となるので,この対象はグループ2に判別される.
5-2.正順変量による判別
固有値と固有ベクトル
線形結合 u = a'x が群間の変動をよく説明するには,
W-1B の固有値と固有ベクトルを用いればよい.
固有値 λi を大きさの順に並べた表をつくると,
表2.正準変量の固有値
| | 第1 | 第2 | 第3 |
|---|
| 固有値 |
0.4340 | 0.1410 | 0.0049 |
|---|
| 寄与率 |
0.7476 | 0.2430 | 0.0093 |
|---|
が得られた.これをみると,第3正準変量の寄与率が非常に低いので,4群の判別には第2正準変量までで
十分であることがわかる.第2正準変量までの固有ベクトル a1,
a2 を求めると,もとの3変量 X1,X2,
X3 に代わる新しい判別用正準変量 U1,U2 が,
| U1 = |
-0.0382 X1 − 0.0372 X2 + 0.0034 X3 |
| U2 = |
-0.0266 X1 + 0.0561 X2 − 0.0211 X3 |
が導入される.正準変量の係数が固有ベクトルである.R のスクリプトを以下に示す.
- nyo.eig <- eigen(solve(w.mat) %*% b.mat) #eigen value
- eq <- t(nyo.eig$vectors) %*% w.mat %*% nyo.eig$vectors
- eq.mat <- matrix(sqrt(diag(eq)), nrow=3, ncol=3, byrow=T)
- nyo.co <- nyo.eig$vectors /eq.mat #standardize
- dimnames(nyo.co) <- list(c("creatine","chloride","choline"), c("cano1","cano2","cano3"))
- nyo.eig$values #display eigen values
- nyo.co #display eigen vectors(canonical variates)
マハラノビス距離と線形判別関数
この2つの正準変量を用いてトレイニングデータの正準得点ベクトルとグループごとの平均ベクトルは,
と計算される.正準得点による郡内平方和積和行列は単位行列になるので,未分類の対象データ
の正準得点 u = (u1,u2)' が与えられたとすると,
グループ j の平均とのマハラノビス距離は,
のようになり,(U1,U2) 平面上では Euclid 距離となる.
先ほどの分類未知のデータ x = (18,5,8)' の正準得点は,
u = (-0.8456,-0.3667)' となるので,各グループ平均とのマハラノビス距離を
求めると,
D12 = 0.03015,D22 = 0.00081,
D32 = 0.00688,D42 = 0.08085
となった.先ほどと同様に,D22 が最も小さいので,
u はグループ2に判別された.
線形判別
関数は,先ほどと同様に
と計算できるので,6個の線形判別関数は,
| W12 = |
0.0366U1 + 0.1420U2 + 0.0683 |
| W13 = |
-0.0166U1 + 0.1113U2 + 0.0147 |
| W14 = |
-0.2422U1 + 0.1012U2 − 0.1424 |
| W23 = |
-0.0532X1 − 0.0307U2 − 0.0536 |
| W24 = |
-0.2788U1 − 0.0408U2 − 0.2107 |
| W34 = |
-0.2256U1 − 0.0101U2 − 0.1570 |
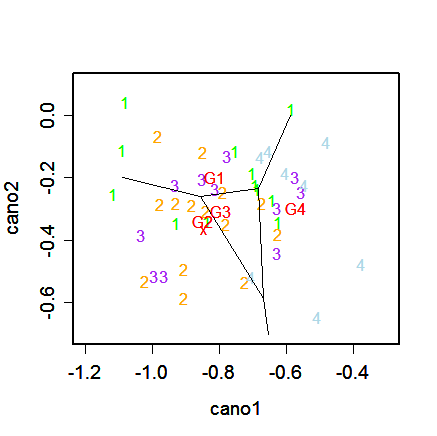
が得られる.直線 Wij = 0 により,(U1,U2) 平面
が4つの部分に分割され,判別の様子を視覚的に表現することができた.
6.サポートベクターマシン
6-1.サポートベクターマシンとは
混合分布からなる母集団分布が完全にわかっている場合には,すでに2-2節でみたように式(2)のような最適な
判別規則が存在する.しかしながら,現実には母集団分布がわかっている場合はほとんどない.最近,2群の判別
方式としてサポートベクターマシン(Support Vector Machine, SVM)が注目されている.サポートベクターマシン
は,現在知られている手法の中では判別性能がよい学習モデルの一つである.これは,未分類のサンプルに対して高い
判別能力をもつ(汎化能力が高い)からである.なお,多群の判別を行うためには複数のサポートベクターマシン
を組み合わせる必要があるが,本稿では扱わない.
6-2.分離超平面とマージン最大化
いま,p 次元空間において,(a・b)
をベクトル a,b 間の内積としたとき,
任意の p 次元変数 x に対して超平面を
(w・x) + b = 0
(17)
とする.ここで,関数 sgn(u) を
sgn(u) = 1,if u ≧ 0,sign(u) = -1,if u < 0
となる符号関数として,判別関数を
f(x) = sgn((w・x) + b)
(18)
と定義する.すなわち,f(x) = 1,のときは x を群1に割り付け,
f(x) = -1,
のときは群2に割り付けるものとする.
ここで,m 個のトレイニングデータ xi,i = 1,…,m,
すべてが式(17)の超平面で分離可能であったとする.すなわち,i が群1由来のときは,
yi = f(xi) = 1,であり,
群2由来のときは,yi = f(xi) = -1,であったとする.
このとき,群間のマージンを最大にする判別関数求める.これは,トレイニングデータを群に分ける超平面
のうち,なるべく間があいた余裕のある超平面を求めようとするものである.
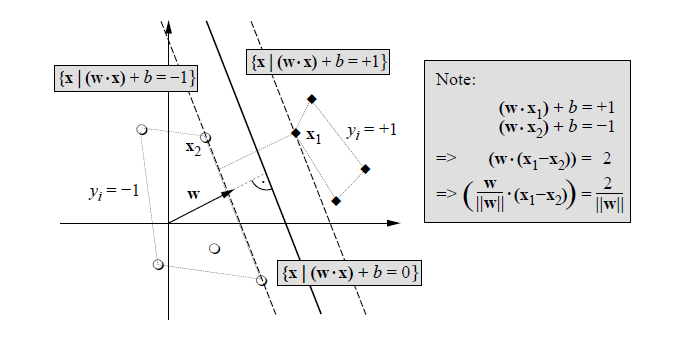
この最適な超平面は下の図に示すように,
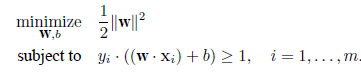 |
(19) |
の最適化問題を解くことによって得られる.
非負のラグランジュ(Lagrange)乗数 α= (α1,…,αm) ≧ 0 を用いて
目的関数を
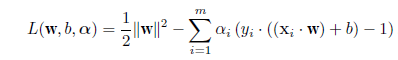 |
(20) |
として,双対問題
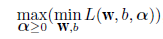 |
(21) |
を解くことに帰着する.すなわち,式(20)を w と b で最小化し,
ラグランジュ乗数 αi で最大化する.
式(20)を w と b で偏微分して 0 とおく,すなわち,
とすると,その解は,
となるので,これを式(20)の目的関数に代入すると,これは以下の最大化問題
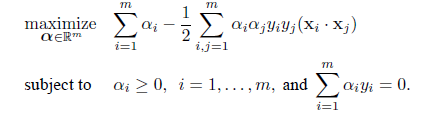 |
(22) |
を満たすラグランジュ乗数 αi を
求めることに帰着する.
この解のうち,αi > 0 となるトレイニングデータは,図のマージン,
(w・x) + b = 1 か
(w・x) + b = -1 上に乗っている.このようなデータを
サポートベクター(Support Vector)と呼んでいる.残りの多くの αi = 0 となるトレイニング
データは式(17)の分離超平面や式(18)の判別関数の構成に関与しない.
6-3.ソフトマージン
実際問題,観測誤差などの影響により,
トレイニングデータが分離超平面で完全に分離されることはあまり期待できない.このため,トレイニング
データでの多少の判別誤りを許すように制約を緩和する方法が考えられている.これを「ソフトマージン」
と呼んでいる.
いま,緩み(slack)変数ξi(≧0)を考え,式(19)の制約条件を
に緩和し,そのもとで目的関数
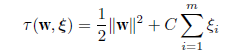 |
(23) |
を最小化する問題になる.ここで,C(>0)は第1項のマージンの大きさと第2項の判別誤りの大きさとの
トレードオフを制御するパラメータである.
参考文献
- Anderson T. W. (1958). An Introduction to Multivariate Statistical Analysis,
John Wiley & Sons, Inc.
- Morrison D. F. (1976). Multivariate Statistical Methods, McGraw-Hill.
- 奥野忠一,久米均,芳賀敏郎,吉沢正(1971).多変量解析法,日科技連.
- 竹内啓,柳井晴夫(1972).多変量解析の基礎,東洋経済新報社.
- 甘利俊一,金明哲,村上征勝,永田昌明,大津起夫,山西健司(2003).
言語と心理の統計−ことばと行動の確率モデルによる分析 統計科学のフロンティア10,岩波書店
Copyright (C) 2007, Hiroshi Omori. 最終更新:2008年10月 5日
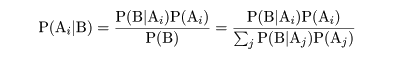
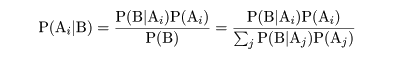
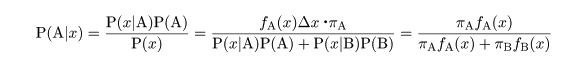
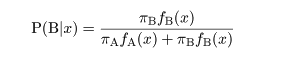
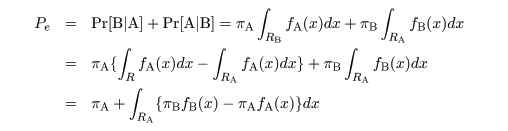
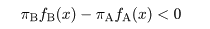
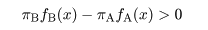



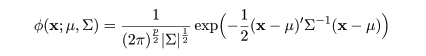
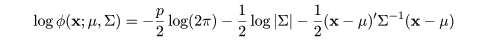
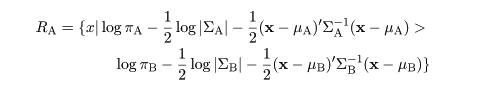
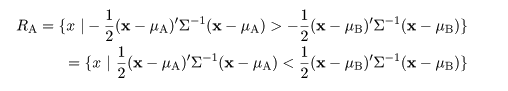
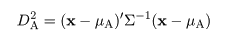
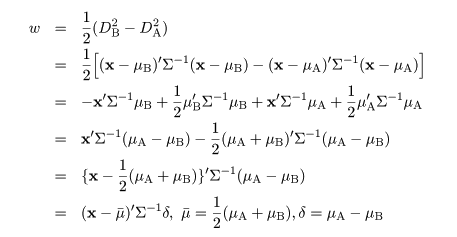
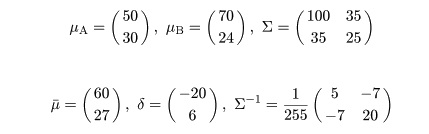
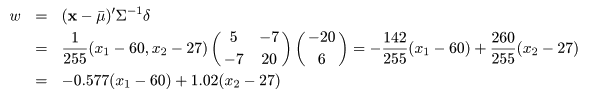

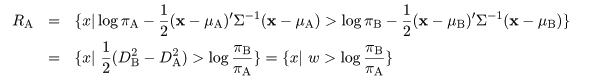 (7)
(7)