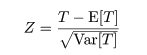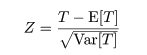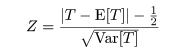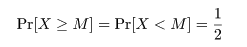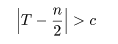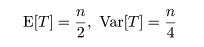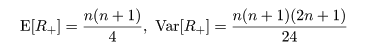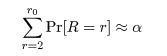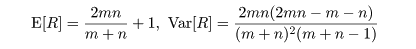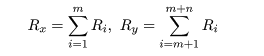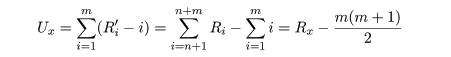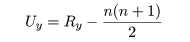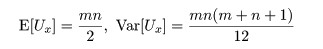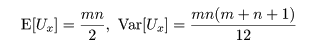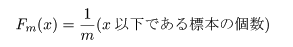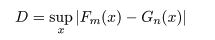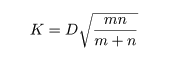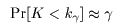2017.11.14
数理統計学演習
ノンパラメトリック検定
東京大学大学院農学生命科学研究科 大森宏
http://lbm.ab.a.u-tokyo.ac.jp/~omori/kensyu/nonpara.htm
1.ノンパラメトリック検定とは
ノンパラメトリック検定(nonparametric test)とは,母集団分布に関して,正規分布などのある特定の分布
を仮定しないで統計的検定を行う方法である.この手法の利点は,多少の制約がある場合もあるが,どのような
母集団分布からのデータであっても適用可能なことである.
このため,
標本中に他の観測値から飛び離れた値と思われる
異常値(outlier)が含まれているような場合でも正しい検定を与えることができる.すなわち,
頑健(robust)な検定法である.
一方,弱点としては,分布に関する情報を用いないので,特定の分布の元での最良の検定(正規母集団での小標本
に対する t 検定など)に比べ検定(検出)力(power)が低下することである.
ノンパラメトリック検定においてはデータの値を直接使わず,これを大きさの順に並べてその順位(rank)を
用いることが多い.このことは,データのもつ情報を全部使い切っていない,情報の損失があることを意味する.
他方,異常値の影響は]それだけ受けにくくなっている.
ノンパラメトリック検定の以前のやり方は,n 個の標本が与えられたときに,なんらかの考え方に基づいて
検定統計量(test statistic)T を求める.n が小さいときには,帰無仮説のもとでの T の分布
が直接計算され,その分布に基づいた数表を用いて検定を行った.n が大きいときは,帰無仮説のもとでの T
の平均 E[T ],分散 Var[T ] を求め,中心極限定理から,
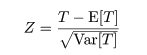
|
(1)
|
が標準正規分布 N(0,1) に近似的に従うことを利用して,標準正規分布表を用いて近似的な検定を行った.
たとえば,両側検定の場合,|Z | の値が 1.96 以上となれば有意水準 0.05 で帰無仮説は棄却される.
なお,T は離散分布となるので近似の精度を上げたいときには分子に 1/2 をいれて,連続性の補正,
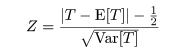
|
(2)
|
を行う.
現在では,オープンソースの統計環境ソフト R にノンパラメトリック検定を行う関数がかなり実装されている
ので,数表をみる必要がないことが多くなった.
使用法としては,標本の正規性に少しでも疑問がもたれるときは"保険"の意味でノンパラメトリック検定を
用いるとよい.この検定で有意と判断されれば非のうちどころはまったくなくなる.
2.1標本問題(one sample problem)
2-1.概要
1つの母集団に関する検定問題である.ある連続分布をもつ母集団から大きさ n の無作為標本
X1,…,Xn が抽出されたとする.ここで,母集団分布の位置母数
(location parameter)に関する両側検定問題
H0 : ξ = ξ0,H1 : ξ ≠ ξ0
(3)
および,片側検定問題
H0 : ξ = ξ0,H1 : ξ > ξ0
(4)
を考えてみよう.正規性の仮定のもとでは,Xi 〜 N( ξ,σ2 ) とおき,
ξ と σ2 の推定量として標本平均 x- と標本不偏分散 s2
を用い,t 検定を行う.
ノンパラメトリック検定では,母集団の位置母数は平均でなくメディアン(中央値)で測られる.これは,
コーシー分布のように平均が存在しない分布にも対応するためである.一方,メディアン M は
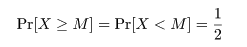
|
(5)
|
と定義されるので,すべての連続分布で存在する.
さてこれからは,一般性を失うことなく ξ0 = 0 とする.ξ0 ≠ 0 のときは,
Xi のかわりに Xi − ξ0 を考えればよい.
また,1標本問題は対のある2標本問題に適用できる.対のある2標本とは,n 組のペアー標本
(X1,Y1 ),…,(Xn,Yn ) から
なる.正規性の仮定のもとでは,
Xi 〜 N( μi,σ2 ),
Yi 〜 N( μi + δ,σ2 )
(6)
と仮定する.ここで興味ある母数は δ であり,μ1,…,μn は攪乱母数(nuisance parameter)
である.Zi = Yi − Xi とおくと
Zi 〜 N( δ,σz2 )
となるので,1標本問題に帰着する.なお,対のある2標本は,正規性の仮定のもとでは反復のない 2×n の2元配置
と考えて解くこともできる.
2-2.符号検定(sign test)
いま,X1,…,Xn のうち正の値(+の符号をもつ)の数を T
とする.ただし,Xi = 0 となる標本が得られたときは,この標本はなかったものとして
取り除いておく.帰無仮説のもとでは式(5)により,T は2項分布 B(n,1/2) に従う.従って,式(3)の
両側検定は
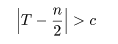
|
(7)
|
という棄却域をつくればよい.c の値は2項分布を計算すれば適当な有意水準に対して正確に
求められる.また,n が大きいときには,
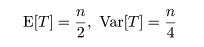
|
(8)
|
となるので,正規近似(1)を行えば任意の有意水準に対して近似的な検定ができる.式(4)の片側検定
に対しては,式(7)の棄却域を片側にとればよい.
メディアンに対する符号検定は 1/2 分位点に対する検定でもある.このことに着目すれば,符号検定
は任意の分位点に対して検定できる.
2-3.Wilcoxon の符号順位和検定(signed rank sum test)
符号検定は,観測値の大小はまったく無視してその符号だけを用いている.これは観測値の情報
をかなり無駄にしていると考えられる.この点を改良したのが Wilcoxon の符号順位和検定である.
しかしながら,母集団分布が対称な分布であるという仮定があらたに加わる.
標本の絶対値 |X | を大きさの順に順位をつけ,これを Ri とおく.
たとえば X1 = 3.1,X2 = -4.5,X3 = 0.9 で
あったならば R1 = 2,R2 = 3,R3 = 1 で
ある.母集団は連続分布を仮定しているので,|Xi| は確率 1 ですべて互いに異なる値
をとり,Ri は一意的に定まる.
しかしながら,実際のデータでは測定精度などや測定値の丸めにより,標本値に同じ値が含まれる
ことがよくある.このような場合をタイ(tie)があるという.タイがあるときは,タイとなったデータ
の順位となり得る値の平均を順位として与えるのが普通である.
たとえば,X1 = 1.5,X2 = -0.3,X3 = 1.5,
X4 = -2.8 であったとする.X1 と X3 は順位
として 2 か 3 を取ったはずである.そこで,この値の平均 2.5 を順位として与える.この結果,
R1 = 2.5,R2 = 1,R3 = 2.5,
R4 = 4 となる.このようにすればタイのあるなしにかかわらず,
ΣRi = n(n+1)/2 となる.また,Xi = 0 というデータが
得られたときはこのデータはなかったものとして取り除いておくのは符号検定法と同じである.
さて,Xi > 0 のときの順位和を R+,
Xi < 0 のときの順位和を R- とおき,この両者のうち小さい
方を T とおく.母集団分布が対称であるので,帰無仮説 H0 : ξ0 = 0
のもとでは R+ と R- の値はほぼ同じで,
ΣRi/2 = n(n+1)/4 に近いことが期待される.よって,T が小さいときには
帰無仮説を棄却することができる.
表1.順位のあり得る組み合わせ(n=4)
| 1 | 2 | 3 | 4 |
R+ | R- |
T |
| + | + |
+ | + |
10 | 0 | 0 |
| − | + |
+ | + |
9 | 1 | 1 |
| + | − |
+ | + |
8 | 2 | 2 |
| + | + |
− | + |
7 | 3 | 3 |
| + | + |
+ | − |
6 | 4 | 4 |
| − | − |
+ | + |
7 | 3 | 3 |
| − | + |
− | + |
6 | 4 | 4 |
| − | + |
+ | − |
5 | 5 | 5 |
| + | − |
− | + |
5 | 5 | 5 |
| + | − |
+ | − |
4 | 6 | 4 |
| + | + |
− | − |
3 | 7 | 3 |
| − | − |
− | + |
4 | 6 | 4 |
| − | − |
+ | − |
3 | 7 | 3 |
| − | + |
− | − |
2 | 8 | 2 |
| + | − |
− | − |
1 | 9 | 1 |
| − | − |
− | − |
0 | 10 | 0 |
T の分布ようすを n = 4 のときに考えてみよう.順位の値は 1,2,3,4 の 4 通り
ある.ある順位をとったデータが正であったか負であっかはまったくの偶然で決まる.そのあり得る
組み合わせは表1に示すように全部で 16 通りである.どの組み合わせも同じ確率で起こるので,
これにより T の分布が決定できる.
たとえば,T = 0 となるのは 2 通りであるので,その確率は 2/16 = 0.125 と計算される.
もし,T = 0 のとき帰無仮説を棄却すると決めたならば,その有意水準は 0.125 となる.
このように T の帰無仮説のもとでの分布を計算すれば,検定の有意確率が求まる.
なお,n が大きいときは,
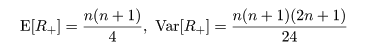
|
(9)
|
となることが知られているので,正規近似(1)を用いて近似的な検定ができる.
2-4.解析例
園芸療法(horticultural therapy)は第2次大戦後,兵士のリハビリテーション等を通して欧米で発達してきた.
日本でも90年代から身体障害者,精神障害者,高齢者等の生活の質(QOL, Quality Of Life)や
セルフエスティーム(self-esteem,自尊感情)を向上させる手段として注目されてきていている.
園芸療法の数値的・客観的な効果の計測を行うため,認知症診断に用いられる
MSE(Mental State Examination,心理機能検査),CDT(Clock Drawing Test,時計描画テスト)と
老年者や認知症患者の日常生活の遂行能力を測る NM スケール(N 式老年者精神状態評価尺度),
N-ADL(N 式老年者日常生活動作能力評価尺度),および,気分の状態(抑うつ,活気のなさ,怒り,疲労,緊張,
混乱)を計測する POMS(Profile Of Mood State),自己記入式 QOL 質問表 QUIK を用いた.
これらの調査を園芸療法の前後でクライアントに対して行い,効果の数値的計測を行った[4,5].
ここでは,MSE の結果についての解析を行う.MSE は 30 点満点で,点数が高いほど日常生活に適応して
いると考えられている.MSE に関しては前後とも回答したクライアントの総数は 19 例であった.
データは表2にまとめられている.元データに差と符号と順位も付け加えた.このデータを用いて,園芸療法
を施す前と後では,心理機能に差がないという帰無仮説,すなわち,
H0:差 = 0
の検定を行う.
データダウンロード
符号検定
差が 0 のデータを取り除くとデータ総数は16となった.16 例のうち,正の符号が 7,負の符号が 6 で
あるので,2項分布を用いて検定が行える.表2のデータが csv ファイル形式
で R の作業フォルダに 'mse.csv' という名前であるとする.符号検定に
対する R のスクリプトは以下のようになる.
-
mse <- read.csv("mse.csv") #データ読み込み
d <- mse$after - mse$before #処方後得点−処方前得点
np <- length(d[d > 0])
nm <- length(d[d < 0])
binom.test(c(np,nm))
結果:'+'の確率 = 0.5625,p 値 = 0.8036 で帰無仮説は棄却されず,
園芸療法が心理機能に変化を引き起こすとは認められなかった.
Wilcoxon の順位和検定
差が 0 のデータを取り除くとデータ総数は16となった.R+ = 86,
R- = 50 となった.検定の R のスクリプトは以下のようになる.
-
wilcox.test(d) # Wilcoxon 検定を行う関数
wilcox.test(mse$after, mse$before, paired=TRUE) # このように記述しても良い
結果:p 値 = 0.363 で帰無仮説は棄却されない.しかし,
-
警告メッセージ:
1: In wilcox.test.default(mse$before, mse$after, paired = TRUE) :
タイがあるため、正確な p 値を計算することができません
2: In wilcox.test.default(mse$before, mse$after, paired = TRUE) :
ゼロ値のため、正確な p 値を計算することができません
という表示が出て何となくすわりが悪い.タイがあるときでも Wilcoxon 検定で
近似的な p 値を出すには,"coin" (Conditional Inference Procedures in a Permutation Test) を”パッケージのインストール”を用いてインストールすれば良い.
-
library(coin) # coin ライブラリー使用宣言
wilcoxsign_test(mse$after ~ mse$before) # タイがあることに対応
wilcoxsign_test(mse$after ~ mse$before, zero.method="Pratt") # 0 に対応
結果:p 値 = 0.395 で帰無仮説は棄却されなかった.
t 検定
比較のために t 検定も行った.
-
t.test(d) # t 検定を行う関数
t.test(mse$after, mse$before, paired=TRUE) # こう書いてもよい.
結果:平均 = 0.895,t 値 = 1.1648(df = 18),p 値 = 0.2593 で帰無仮説は棄却されなかった.
データの吟味
今回の調査では,クライアント全体では園芸療法の効果は認められなかった.また,MSE の満点が30点なので,
元々心理機能に問題がなく満点近い得点のクライアントでは,効果が認められないのも当然といえる.
その上,園芸療法処方の前後で半年
程度のタイムラグがあるので,何もしなくても認知症の症状が進行する場合もあり,効果が検出しずらい
こともある程度予測できる.そこで,データをよく調べるため,差と年齢のプロットを図1に行った.
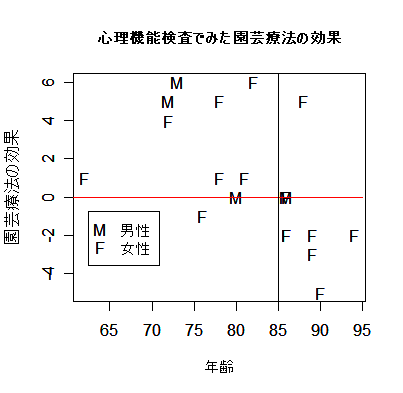
図1.園芸療法の”効果”と年齢との関係
これをみると,年齢が高いほど効果が減少しているようにみえる.そこで,多少「後づけ」ではあるが
クライアントのうち若年層( 85 歳以下)を取り出すことにした.若年層は 10 例となり,サンプルサイズは
かなり小さくなった.
符号検定
表3のデータで帰無仮説の検定を行う.R のスクリプトは以下の通り.
-
young <- which(mse$age<86) # 年齢86歳未満のデータ番号を取得
d2 <- d[young]
np <- length(d2[d2 > 0])
nm <- length(d2[d2 < 0])
binom.test(c(np,nm))
結果:'+'の確率 = 0.8889,p 値 = 0.03906 で,帰無仮説は 5%有意で棄却された.これより,
高齢でない層では,園芸療法が心理機能に変化を引き起こすと認められた.
Wilcoxon の順位和検定
R+ = 42.5,R- = 2.5 となった.
R のスクリプトは以下の通り.
-
wilcox.test(d2)
wilcoxsign_test(mse$after[young] ~ mse$before[young], zero.method="Pratt")
結果:p 値 = 0.01563 で帰無仮説は 1% 有意ではないが,5% 有意で棄却された.
t 検定
-
t.test(d2)
t.test(mse$after[young], mse$before[young], paired=TRUE)
結果:平均 = 2.8,t 値 = 3.3308(df = 9),p 値 = 0.008788 で帰無仮説は
1% 有意で棄却された.
2-5.検出力(power)の違い
実際の検定を行うときに,t 検定を用いるかノンパラメトリック検定を用いるか迷うことがあると思う.
現在では,シミュレーションにより検定の実力を比較簡単に調べることができる.状況としては,正規分布より
平均から離れた値の出やすい t 分布を考え,データが的正規性からはずれたときでもどの程度の検出力があるか
調べる.
まず,帰無仮説が正しいときの棄却確率(有意水準)を調べる.これが 5 %などの名目上の確率を上回る
検定は推奨されない.また,名目上の確率を大きく下回る検定は保守的(conservative)であると考えられるので
あまりよくない.
次に,帰無仮説が正しくないときの棄却確率(検出力)を調べる.この棄却確率が最も高いのが良い検定方式
であると言える.
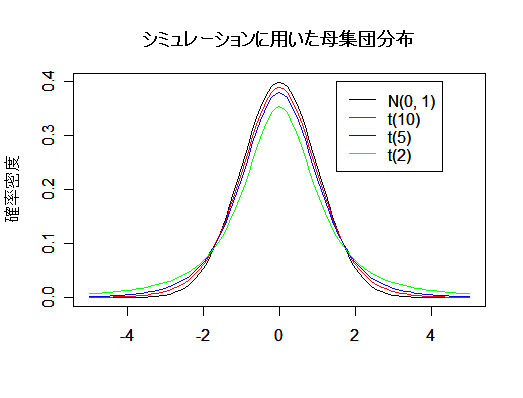
まず母集団分布として,
標準正規分布 N(0, 1),自由度 10 の t 分布 t(10),自由度 2 の t 分布 t(2) を考える.t(10) は正規分布より
少し裾が重いが,t(2) は裾が大変重く,極端に大きな値や小さな値が出やすくなっている.
シミュレーションの概要
-
まず,データ数が n = 10 のときを考える.帰無仮説が真であるとする.すなわち,母集団平均 m = 0 である.
この母集団から n 個の正規乱数 x を抽出し,そのデータに対し符号検定と Wilcoxon の順位和検定,
t 検定を行い,それぞれの p 値を出す.
| n <- 10 | # サンプルサイズ |
|
m <- 0
| # 真の平均 |
|
x <- rnorm(n, mean=m)
| # 標準正規乱数 n 個 |
|
np <- length(x[x > 0])
| # x > 0 となる個数 |
|
nm <- length(x[x < 0])
| # x < 0 となる個数 |
|
x
| # データ |
|
binom.test(c(np,nm))$p.value
| # 符号検定の p 値 |
|
wilcox.test(x)$p.value
| # Wilcoxon の順位和検定 p 値 |
|
t.test(x)$p.value
| # t 検定の p 値 |
次に,データが正規分布に従っていない場合を考える.自由度 d = 10 と 2 の t 分布
とした場合の符号検定と Wilcoxon の順位和検定,
t 検定を行い,それぞれの p 値を出す.
|
x0 <- x
| # 標準正規分布 |
|
x <- rt(n, df=2) + m
| # 自由度 2 の t 分布 |
|
xx <- data.frame(cbind(x0, x))
| # |
|
names(xx) <- c("N(0, 1)", "t(2)")
| # 変数名の定義 |
|
stripchart(xx, ylim=c(0.5,2.5))
| # 乱数の分布範囲の表示 |
|
title(main="乱数標本の例")
| # |
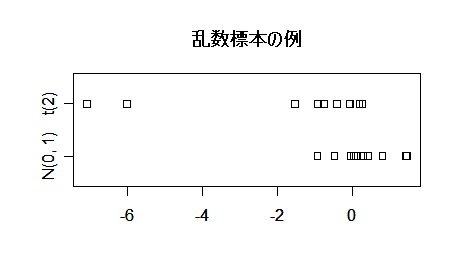
以下に,乱数のサンプルサイズ n と平均 m と t 分布のときの自由度 d から
N = 10000回のシミュレーションにより,
検定ごとに p 値が 5%や 1%以下になる頻度を算出する関数を定義する.
|
srst.f <- function(m, n, d=NULL){
| # 関数定義:平均 m,サンプル数 n,自由度 d |
|
N <- 10000
| # シミュレーション回数 |
|
yb <- NULL; yw <- NULL; yt <- NULL
| # p 値格納ベクトルの定義 |
|
for(i in 1:N){
| # |
|
if(is.null(d)) x <- rnorm(n, mean=m)
| # d の値がないときは正規乱数 |
|
else x <- rt(n, df=d) + m
| # そうでないときは自由度 d の t 分布乱数 + m |
|
np <- length(x[x > 0])
| # 乱数で x > 0 の個数 |
|
nm <- length(x[x < 0])
| # 乱数で x < 0 の個数 |
|
yb <- c(yb, binom.test(c(np,nm))$p.value)
| # 符号検定の p 値を順に格納 |
|
yw <- c(yw, wilcox.test(x)$p.value)
| # Wilcoxon の順位和検定 p 値を順に格納 |
|
yt <- c(yt, t.test(x)$p.value)
| # t 検定の p 値を順に格納 |
|
}
| # |
|
b <- length(yb[yb<0.05])/N
| # 符号検定の p 値が 0.05 未満の個数 |
|
w <- length(yw[yw<0.05])/N
| # Wilcoxon の順位和検定 p 値が 0.05 未満の個数 |
|
t <- length(yt[yt<0.05])/N
| # t 検定の p 値が 0.05 未満の個数 |
|
q5 <- c(t, w, b)
| # |
|
b <- length(yb[yb<0.01])/N
| # 符号検定の p 値が 0.01 未満の個数 |
|
w <- length(yw[yw<0.01])/N
| # Wilcoxon の順位和検定 p 値が 0.01 未満の個数 |
|
t <- length(yt[yt<0.01])/N
| # t 検定の p 値が 0.01 未満の個数 |
|
q1 <- c(t, w, b)
| # |
|
return(rbind(q5, q1))
| # |
|
}
| # |
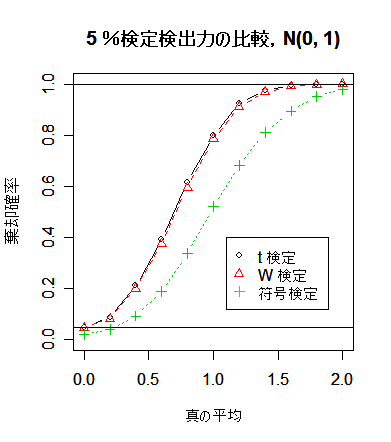
まず,母集団が正規分布のとき,平均を 0 から 0.2 ずつ 2 まで変化させて,検定
方式ごとに有意水準 5 %検定と 1 %検定を行ったときの棄却確率をグラフ化すると,
検出力の変化と違いがよくわかる.以下のスクリプトを少し変えて,引き続き母集団が t 分布のときの検出力の
グラフを出してみよう.
|
mv <- seq(0, 2, by=0.2)
| # 母集団平均の定義 |
|
resnorm5 <- NULL
| # 5 %検定を行ったときの棄却確率行列 |
|
resnorm1 <- NULL
| # 1 %検定を行ったときの棄却確率行列 |
|
for(i in 1:length(mv)){
| # |
|
s <- srst.f(mv[i], 10)
| # 平均 mv[i] の正規乱数(t 分布のときは,srst.f(mv[i], 10, d) とする) |
|
resnorm5 <- rbind(resnorm5, s[1,])
| # |
|
resnorm1 <- rbind(resnorm1, s[2,])
| # |
|
}
| # 行列データの同時プロット |
|
matplot(mv, resnorm5, type="b", pch=1:3, ylim=c(0,1), xlab="真の平均", ylab="棄却確率")
|
|
abline(h=0.05); abline(h=1)
| # 有意水準(0.05)と確率 1 のライン |
|
legend(1.1,0.4,c("t 検定","W 検定","符号検定"), pch=1:3,col=c("black","red","green"))
|
|
title(main="5 %検定検出力の比較,N(0, 1)")
| # |
真の平均 m = 1 のときの母集団分布と検定法による検出力の比較
| | N(0, 1) | t(10) |
t(5) | t(2) |
|---|
| t 検定 | 0.7989 | 0.7296 |
0.6395 | 0.4135 |
|---|
| Wilcoxon の順位和検定 | 0.7830 | 0.7187 |
0.6391 | 0.4616 |
|---|
| 符号検定 | 0.5121 | 0.4761 |
0.4370 | 0.3428 |
|---|
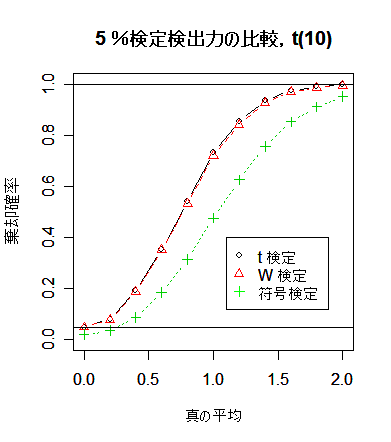
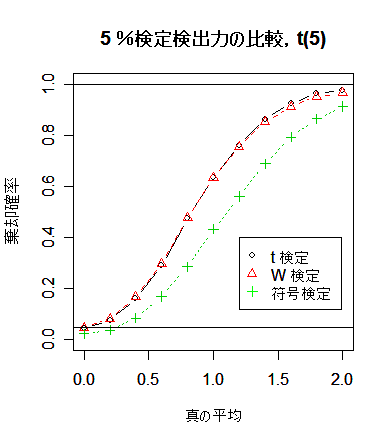
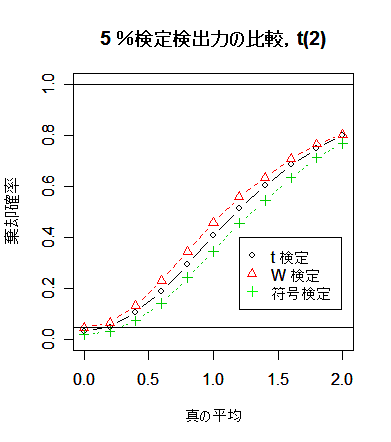
シミュレーションの結果,符号検定の検出力は予想されたように,かなり低い.一方,
t 検定と Wilcoxon の順位和検定では検出力がほとんど変わらない.Wilcoxon の順位和検定のロバスト性が
生きてくるのは自由度 2 の t 分布という相当裾の重い分布になってからである.裾がそれほど重くない
ときは,t 検定の方が検出力がわずかとはいえ高いので,t 検定を使用してよいように思える.
標本の大きさ n を増やしたときも調べてみるとよいだろう.
データ分布の左右の対称性の「ずれ」に対する検出力の違いは,ガンマ分布などを使用したシミュレーションが
必要であろう.
3.2標本問題(two sample problem)
3-1.概要
2つの母集団から無作為標本 X1,…,Xm,
Y1,…,Yn が抽出されたとする.
等分散の正規性の仮定のもとでは,
Xi 〜 N( μx,σ2 ),
Yj 〜 N( μy,σ2 )
(10)
と仮定し,帰無仮説は,
H0 : μx = μy
(11)
となる.標本平均 X-,Y- とこみにした標本不偏分散 s2
を用いて t 検定を行う.
ノンパラメトリック検定においては,無作為標本 Xi,Yj がそれぞれの
累積分布関数 Fx(・),Fy(・) から抽出されたと考える.帰無仮説は,
すべての z に対して
H0 : Fx(z ) = Fy(z )
(12)
となる.
3-2.連検定(run test)
2つの母集団分布間のいかなる差も検出できる.n = 20 程度では t 検定の 75% ぐらいの検出効率である.
標本 X1,…,Xm,
Y1,…,Yn をまとめて大きさの順に並べたものを考える.たとえば
m = 4,n = 5 のデータが帰属母集団により,
y, x, x, y, x, y, y, y, x
と並べられたとする.このデータは,1 つの y の連から始まり,次に 2 つの x の連が
続き,さらに 1 つの y の連が続くというようにして全体で 6 つの連がある.もし 2 つの母集団
が同一であるならば x と y は混ざり合い,連の総数は大きくなると考えられる.逆に,
2 つの母集団分布が大きく離れているときは,極端な場合には連の総数は 2 しかない.このことから連の
総数を R として,R がある特定の値 r0 より小さいときに帰無仮説
を棄却するという検定方式が考えられる.r0 の値は以下のように考えて求められる.
帰無仮説のもとでは,可能な m 個の x と n 個の y の並び方はすべて等確率で起こる.
そのような並び方は全部で m+nCm 通りある.連の総数のうち x が
つくる連の数と y がつくる連の数は等しいか,どちらかが 1 つ少ない場合に限られるので,
連の総数の実現値 r が偶数と奇数の場合に分けて考えればよい.
r = 2k となる並び方の場合の数を考える.このときは,k 個の x の連と
k 個の y の連がある.k 個の x の連をつくるにはまず m 個の x を k 個の
グループに分けねばならない.これは m 個の x の間の m−1 個のスペースに k−1 個の
デバイダーを挿入することで得られる.このやり方は m-1Ck-1 通りある.
同様に k 個の y の連は n-1Ck-1 通りある.
これらの k 個の x の連と k 個の y の連は組み合わされ,また,最初の連が x から
始まるか y から始まるかの 2 通りを考慮すると,全体で r = 2k 個の連ができる場合の数
は 2×m-1Ck-1×n-1Ck-1 通りある.
よって,r = 2k 個の連ができる確率は,
となる.同様に r = 2k+1 の場合は,
となる.
ほぼ有意水準 α の検定を行うには,
となるような r0 をみつければよい.
なお m,n が大きいときは,
となることが知られているので,正規近似(1)により近似的な検定ができる.この近似は m と n がともに 10 を
超えればかなりよいことも知られている.
連検定は 2 つの母集団分布間の位置のみならず,形の差にも反応する.2 つの分布が同じメディアンをもっている
が,X の分布は真ん中に集まっているが,Y の分布が拡がっているときを考えると,連の最初と
最後の方に長い連ができやすくなり,このことが連の総数を減少させるからである.
なお,R で連検定を行うには,"tseries" (Time series analysis and computational finance) ライブラリーをインストールしておけば利用できる.
-
library(tseries)
# y, x, x, y, x, y, y, y, x
a <- c(0,1,1,0,1,0,0,0,1)
a <- factor(a)
runs.test(a)
3-3.Mann-Whitney の U 検定
順位和検定(rank-sum test)とも呼ばれる.2 つの母集団分布の平均的な位置の違いを検出する方法である.
ある程度大きな標本数では t 検定の約 95% の検出効率である.
標本 X1,…,Xm,
Y1,…,Yn をまとめたものを Zi,i=1,…,m+n と
表す.すなわち,
Zi = Xi,i=1,…,m,
Zi+m = Yi,i=1,…,n
である.ここで,Z を小さいものから順に順位をつけこれを Ri とおく.もし,
タイがあったときは前節と同様に平均順位を割り付ける.ここで,
とおく.すなわち,Rx は Xi の順位の和であり,
Ry は Yi の順位の和である.
Rx + Ry = (m+n+1)(m+n)/2 である.
さて,Ux を X が Y より大きくなる個数とする.いま,
Xi の順序統計量(大きさの順に並べたもの)を,
X1',…,Xm' とし,これに対応する順位を
R1',…,Rm' とおく.明らかに X1' は
R1'−1 個の Y より大きく, X2' は
R2'−2 個の Y より大きい.同様に考えて, Xm' は
Rm'−m 個の Y より大きい.よって,
となる.同様に,
であり,Ux + Uy = mn が成立する.検定統計量 U は
Ux と Uy のうち小さい方とする.X の分布と
Y の分布が離れていれば U の値は小さくなるはずである.
m,n の値が大きいときは,式(12)の帰無仮説のもとで,
または,
となることが知られているので,正規近似(1)を行って検定することができる.なお,この正規近似は m,n が
7 より大きければかなり正確であることも示されている.
3-4.Kolmogorov-Smirnov の 2 標本検定
累積分布関数 F(・),G(・) をもつ 2 つの母集団からそれぞれ大きさ m,n の無作為
標本 X1,…,Xm, Y1,…,Yn
が抽出されたとする.このとき,
を経験(標本)累積分布関数という.標本 Yi に対する経験累積分布関数を
Gn(x ) としたとき,2 つの母集団からの経験累積分布の最大偏差
を求める.次に,
を求め,これを検定統計量として用いる.
2 つの母集団の累積分布関数が等しいという帰無仮説のもとでの K の漸近分布
(m,n → ∞ としたときの分布)から以下で定義される臨海値が求められている.すなわち,
であり,この値は表3に示されている.
表3.Kolmogorov-Smirnov 2 標本両側検定の臨界値
| 確率:γ |
0.99 | 0.95 | 0.90 |
0.85 | 0.80 |
| 臨界値:kγ |
1.63 | 1.36 | 1.22 |
1.14 | 1.07 |
3-4.解析例
前節では,心理機能検査(MSE)データを対のある 2 標本データとして解析した.この節では,
このデータの園芸療法前データを対照とし,園芸療法後データを処理とみなして解析してみる.この場合,
実際とは異なりこのデータの解析法としては正しくないが,
対照 19 名,処理 19 名のデータとみなすわけである.
データ分布
対照区と処理区とのデータ分布の違いを箱ひげ図でみる.R のスクリプトは以下のようになる.これを
見ると,対照区と処理区で分布に大きな違いがないようにみえる.検定で確認してみよう.
-
boxplot(mse$before, mse$after, names= c("対照区","処理区"), ylab="MSE 得点", cex.axis=0.8)
連検定
R のスクリプトは以下の通り.
-
nrow(mse)
score <- c(mse$before, mse$after)
treat <- factor(rep(c(0,1), each=nrow(mse)))
o <- order(score)
score[o]
treat[o]
library(tseries)
runs.test(treat[o])
結果:p 値 = 0.5106 で帰無仮説は棄却されない.
Mann-Whitney の U 検定
R のスクリプトは以下の通り.
-
wilcox.test(mse$after, mse$before)
wilcox.test(score ~ treat)
library(coin)
wilcox_test(score ~ treat)
タイがあるときは、"coin" を用いる.
結果:p 値 = 0.6705 で帰無仮説は棄却されない.
t 検定
R のスクリプトは以下の通り.
-
t.test(mse$after, mse$before, var.equal=T)
t.test(score ~ treat, var.equal=T)
結果:t 値 = 0.3725(df = 36),p 値 = 0.7117 で帰無仮説は棄却されない.
Kolmogorov-Smirnov 検定
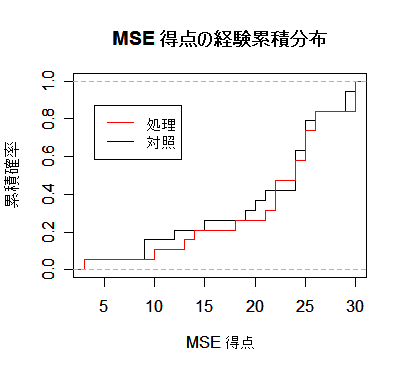
まず,対照区と処理区の経験累積分布の重ね合わせのグラフを書き,両者の乖離の程度をみて検定を行う.
R のスクリプトは以下の通り.
-
plot(ecdf(mse$before), do.points=F, verticals=T,xlab="MSE 得点",
ylab="累積確率", xlim=range(mse$after,mse$before), main="")
plot(ecdf(mse$after), do.points=F, verticals=T, add=T, col.h='red', col.v='red')
title(main="MSE 得点の経験累積分布")
legend(locator(1), legend=c("処理","対照"), lty=c(1,1),col=c("red","black"))
ks.test(mse$after, mse$before)
legend の "locator(1)" は、グラフをクリックするとそこに凡例が表示される.
結果:D = 0.10526,p 値 = 0.9999 で帰無仮説は棄却されない.経験累積分布をみても両者はほとんど
重なっている.
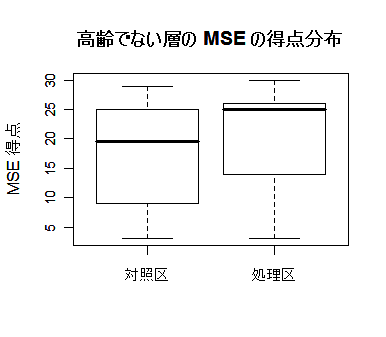
「若年層」のデータ分布
前節の解析では,「若年層」のデータでは,園芸療法の効果の有意性が示された.対照区と処理区とみなした場合
はどうなるか試してみる.R のスクリプトは以下の通り.これをみると,処理区の方が若干上の方にシフトしている
ようにみえる.検定で確認する.
-
boxplot(mse$before[young], mse$after[young], names= c("対照区","処理区"), ylab="MSE 得点", cex.axis=0.8)
title(main="高齢でない層の MSE の得点分布", cex.main=1.0)
連検定
R のスクリプトは以下の通り.
-
young <- which(mse$age<86)
yscore <- c(mse$before[young], mse$after[young])
ytreat <- factor(rep(c(0,1), each=length(young)))
oy <- order(yscore)
yscore[oy]
treat[oy]
library(tseries)
runs.test(treat[oy])
結果:p 値 = 0.7389 で帰無仮説は棄却されない.
Mann-Whitney の U 検定
R のスクリプトは以下の通り.
-
wilcox.test(mse$after[young], mse$before[young])
library(coin)
wilcox_test(yscore ~ ytreat)
結果:p 値 = 0.4228 で帰無仮説は棄却されない.
t 検定
R のスクリプトは以下の通り.
-
t.test(mse$after[young], mse$before[young], var.equal=T)
t.test(yscore ~ ytreat, var.equal=T)
結果:t 値 = 0.7368(df = 18),p 値 = 0.4707 で帰無仮説は棄却されない.
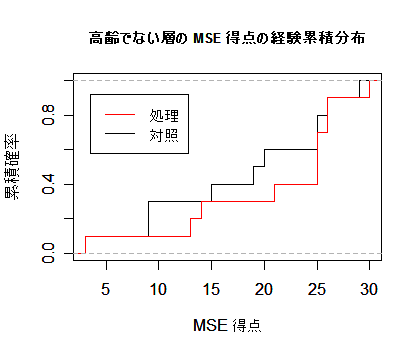
Kolmogorov-Smirnov 検定
まず,対照区と処理区の経験累積分布の重ね合わせのグラフを書き,両者の乖離の程度をみて検定を行う.
R のスクリプトは以下の通り.
-
plot(ecdf(mse$before[young]), do.points=F, verticals=T,xlab="MSE 得点",
ylab="累積確率", xlim=range(mse$after[young],mse$before[young]), main="")
plot(ecdf(mse$after[young]), do.points=F, verticals=T, add=T, col.h='red', col.v='red')
title(main="高齢でない層の MSE 得点の経験累積分布", cex.main=0.8)
legend(locator(1), legend=c("処理","対照"), lty=c(1,1),col=c("red","black"))
ks.test(mse$after[young], mse$before[young])
結果:D = 0.3,p 値 = 0.7591 で帰無仮説は棄却されない.
経験累積分布をみると,両者に多少の「ずれ」が認められるが,有意な「ずれ」ではなかった.
1元配置のノンパラメトリック検定
1元配置の場合のノンパラメトリック検定は,クラスカル・ウォリス順位和検定が
知られている.R には kruskal.test という関数で実行できる.
- 品種によるコメの収量の違い
水稲の9品種をそれぞれ,6区画の水田で栽培したときのアール当たりの玄米重量は以下のようであった.
このうち,A,B,D,それぞれ,同じ母本から育成された品種であり,C は標準(対照 control)品種である.
このデータは一元配置分散分析で解析できる.処理が品種で,9 水準からなっている.帰無仮説は,
H0:収量はどの品種も同じである
である.
データダウンロード
yy <- read.csv("hinsyu.csv"); yy
n <- nrow(yy) # 繰り返し数
a <- ncol(yy) # 処理数
y <- as.vector(as.matrix(yy)) # データのベクトル化
x <- factor(rep(1:a, c(rep(n,a)))) # データのラベル
cbind(y, x)
summary(aov(y ~ x)) # 一元配置分散分析
#
kruskal.test(y, x) # クラスカル・ウォリス順位和検定
参考文献
- Mood A. M., Graybill F. A. & Bose D. C. (1974). Introduction to the Theory of Statistics,
McGraw-Hill.
- Sokal R. R., & Rohlf F. J. (1981). Biometry, 2nd. ed., W. H. Freeman & Company.
- 石井進(1971)."生物統計学入門",培風館.
- 鈴木修(編),大森宏,児玉良治,渡辺俊之,矢野広,山根健治(2004).
専修学校における園芸療法士教育育成システムの研究開発
(文部科学省委託平成15年度「専修学校先進的教育研究開発事業」)
- 鈴木修,渡辺俊之,矢野広,山根健治,大森宏,伊東正信,最上正秀,山下容子,小泉力,
児玉良治,頭士智美,細井薫,水口聡子,遠藤久子,樋田奈穂子,小島ユリ,郡司敏幸(2005).
福祉サービス提供者に対する園芸療法教育システムの研究開発
(平成16年度文部科学省「専修学校社会人キャリアアップ教育推進事業」)
- 竹村彰通(1991)."現代数理統計学",創文社.
Copyright (C) 2007, Hiroshi Omori. 最終更新:2017年10月 3日