判別分析

数理統計学演習

判別分析（質問への解答）

東京大学大学院農学生命科学研究科　大森宏

質問の内容（要約）

3 グループからなる集団の 9 変数の測定データに基づいて、SPSS で判別分析を行ったが何をやっているのか不明。特に、以下の２点がわからない。

グループ数が３のとき判別関数の個数が２になった理由。
変数選択をステップワイズ法で行ったが、選択された変数が判別関数で同じものだった理由。

１．判別関数の個数について

　判別関数は２つのグループ間の判別に用いる関数で、一般に g 個のグループがあった場合は、g(g - 1)/2 の判別関数が作れます。
　正準判別における正準変量の最大次元は、判別に用いる変数の数とグループ数 - 1 の小さい方の数まで作れます。
　質問者は判別関数の個数と正準変量の最大次元とを混同されたと思います。

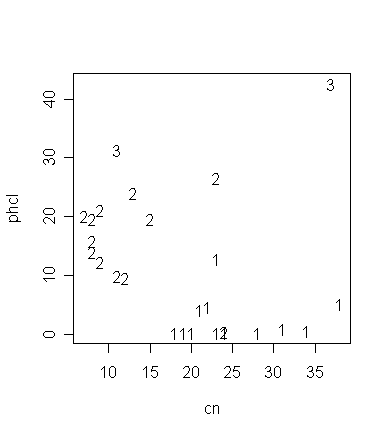
わかりやすくするために R を使って解析した例を紹介します。変数 cn、phcl の値とサンプルのグループ帰属が group で以下のように示されているとします。

cn phcl group [1,] 34 0.5 1 [2,] 28 0.2 1 [3,] 24 0.2 1 [4,] 23 0.3 1 [5,] 19 0.3 1 [6,] 20 0.2 1 [7,] 24 0.4 2 [8,] 23 26.6 2 [9,] 13 24.1 2 [10,] 15 19.7 2 [11,] 38 5.1 1 [12,] 21 4.2 1 [13,] 12 9.6 2 [14,] 18 0.3 1 [15,] 23 12.9 1 [16,] 31 1.0 1 [17,] 37 42.6 3 [18,] 8 19.6 2 [19,] 7 20.2 2 [20,] 9 21.1 2 [21,] 8 14.0 2 [22,] 8 15.8 2 [23,] 9 12.3 2 [24,] 11 31.4 3 [25,] 22 4.6 1 [26,] 11 9.9 2

これを散布図で表示すると、

となり、この変数の組で判別が行えそうな気がします。これを、MASS ライブラリーにある lda 関数を用いて正準判別を行うと、変数の数が２で、グループ数 - 1 も２なので、以下のように、２つの正準変量　LD1 と LD2 が得られます。
　Proportion of trace:から、LD1 に大きな判別力があることがわかります。

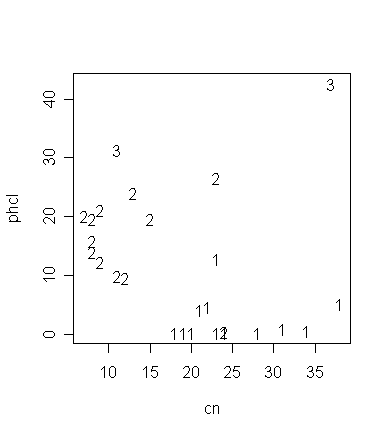
> library(MASS) > z <- lda(group ~ cn + phcl) > z Call: lda(group ~ cn + phcl) Prior probabilities of groups: 1 2 3 0.46153846 0.46153846 0.07692308 Group means: cn phcl 1 25.08333 2.483333 2 12.25000 16.108333 3 24.00000 37.000000 Coefficients of linear discriminants: LD1 LD2 cn 0.05613327 -0.13082789 phcl -0.16064435 -0.05322542 Proportion of trace: LD1 LD2 0.8536 0.1464

　次に、正準変量平面でのデータの分布を見ます。predict 関数でグループの帰属を緑色で表示しました。

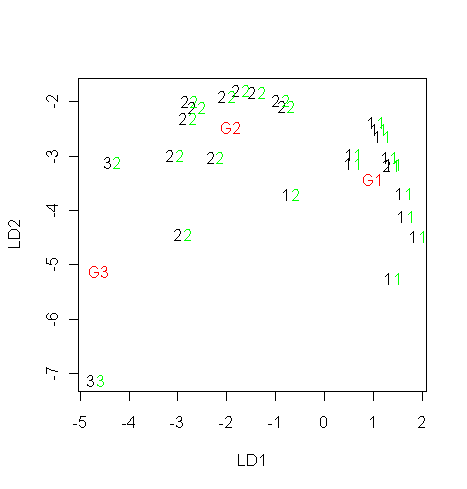
> x <- cbind(cn, phcl) > z$scaling # 正準変量固有ベクトル LD1 LD2 cn 0.05613327 -0.13082789 phcl -0.16064435 -0.05322542 > u <- x %*% z$scaling # 正準変量平面への変換 > plot(u, type="n") > text(u, as.character(group)) > um <- z$means %*% z$scaling # 正準変量平面上でのグループ平均 > text(um, c("G1","G2","G3"), col="red") > pg <- predict(z) > up <- u > up[,1] <- up[,1]+0.2 > text(up, as.character(pg$class), col="green") # グループ帰属を緑で表示

　正準変量平面での判別関数は、グループの存在確率を考慮しない場合は、グループ平均の垂直２等分線になります。Rではデフォルトで、グループ存在確率を考慮に入れた判別を行っているので、グループ２とグループ３の判別では、グループ３の平均近くまでグループ２と判別します。このため、SPSS の結果とはずれているかと思います。

２．判別関数（正準変量）で選ばれた関数について