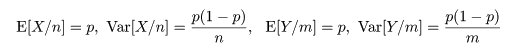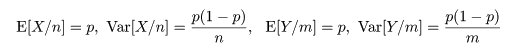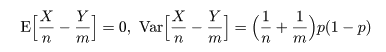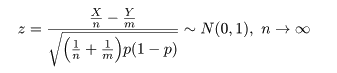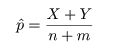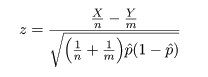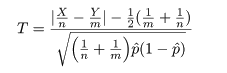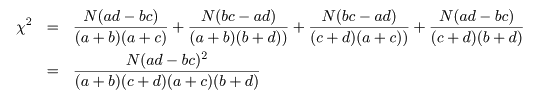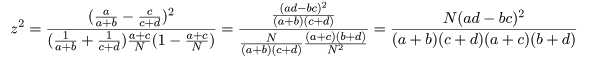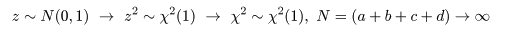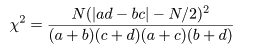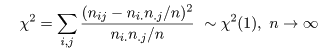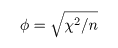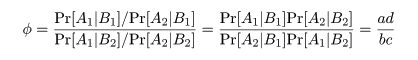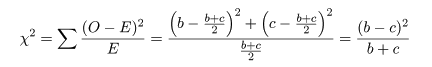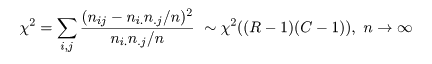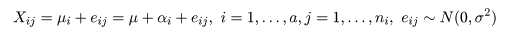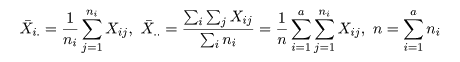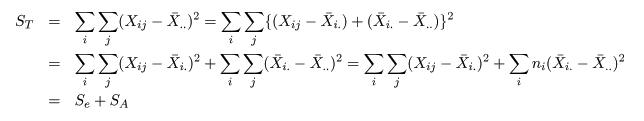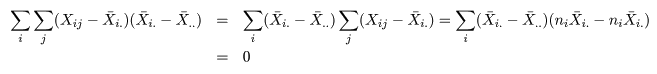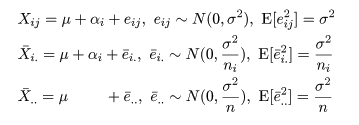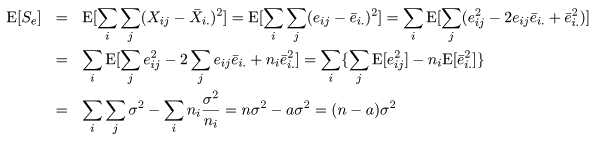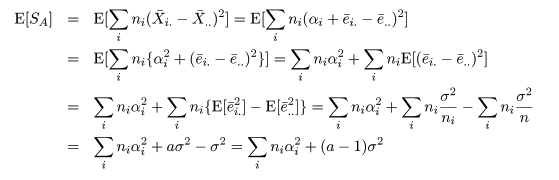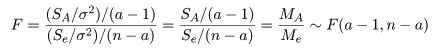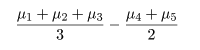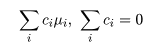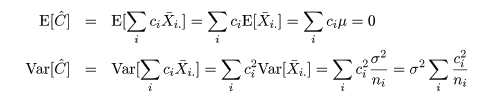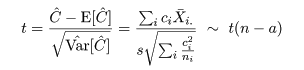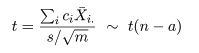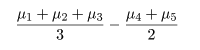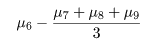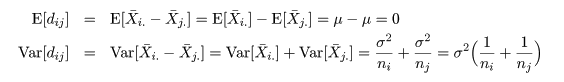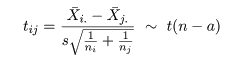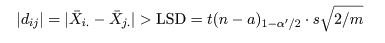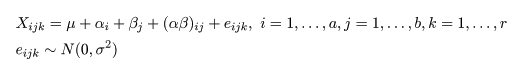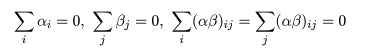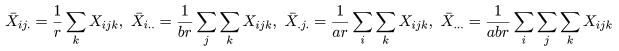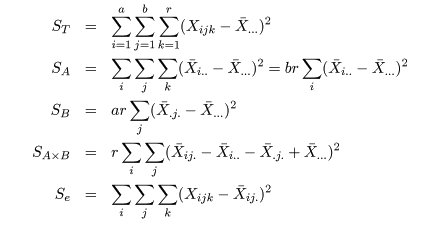東京国際大学大学院

心理データ解析（後期）

東京大学大学院農学生命科学研究科　大森宏

１．分割表の解析

成功確率（比率）の同等性の近似検定

• 勝率の同等性の検定
  　前節では，A と B で将棋を 10 試合行い，A が 7 勝 3 敗の成績 だったときに，A と B で将棋の強さに違いがあると言えるかの検定を行った．続いて， A と B で囲碁を 10 試合行い，A が 4 勝 6 敗の成績であったとする．このとき， A の B に対する将棋の強さと囲碁の強さとで違いがあるかの検定を行う．帰無仮説は，
  H₀：A の B に対する将棋の勝率 ＝ A の B に対する囲碁の勝率
  である．

  # 勝率同等性検定の R スクリプト

  r <- c(7, 4)	# A の将棋の勝数と囲碁の勝数
  n <- c(10, 10)	# 将棋の試合回数と囲碁の試合回数
  prop.test(r, n, correct=F)	# 比率の同等性検定（連続性の補正なし）
  prop.test(r, n)	# 比率の同等性検定（連続性補正）

  課題： 勝敗の比率はそのままで，試行回数を増やして（n = 30）同様な検定を行え．

２×２分割表

2 × 2 分割表データ

	成　功	失　敗	計
試行 X	a	b	a + b
試行 Y	c	d	c + d
計	a + c	b + d	N

帰無仮説のもとでの期待度数

	成　功	失　敗
試行 X	(a + b)(a + c)/N	(a + b)(b + d)/N
試行 Y	(c + d)(a + c)/N	(c + d)(b + d)/N

となる．ここで，ピアソン（Pearson）のχ² 値，

• 勝率同等性の χ² 検定
  

  # 勝率同等性ピアソン χ² 検定の R スクリプト

  x <- matrix(c(7, 3, 4, 6), nc=2, byrow=T)	# A の将棋の勝ち負け数と囲碁の勝ち負け数の行列
  shogi <- c(7, 3)	# A の将棋の勝ち負け数
  igo <- c(4, 6)	# A の囲碁の勝ち負け数
  x <- rbind(shogi, igo)	# 行連結による行列化
  chisq.test(x, correct=F)	# 勝率同等性 χ2 検定（連続性の補正なし）
  chisq.test(x)	# 勝率同等性 χ2 検定（連続性の補正）

  課題： 勝敗の比率はそのままで，試行回数を増やして（n = 30）同様な検定を行え．

  課題：ビデオリサーチ社のデータによると，関西地区において，NHK 大河ドラマ07年の「風林火山」の 初回視聴率は16.2％であったが，08年の「篤姫」の初回視聴率は19.8％であった．調査対象者がどちらも600名 であったとすると，関西地区で大河ドラマの人気に変化があったかどうか，検定せよ．
  　なお，関東地区では「風林火山」の初回視聴率は21.3％で，「篤姫」の初回視聴率は20.3％であった．

• イエーツ（Yates）の連続性の補正の効果
  　χ² 検定ではイエーツの連続性補正を行った方が χ² 分布への 近似がよいとされている．R でもデフォルトでは連続性の補正を行うことになっていて，連続性 の補正をはずすには，そのように指定しなければならない．
  　補正の効果をシミュレーションでみてみよう．成功確率がどちらも p = 0.4 として，n = 30 の二項分布乱数を ２回発生させると 2 × 2 分割表ができ，χ² 値が計算される．これを N = 10000 回繰り返して その分布をみればよい．
  　特に問題となるのは，帰無仮説が棄却される（第１種の過誤）確率である．これが 名目の 5％より大きな検定は危険（有意になりやすい）であり，推奨されない．また，5％よりかなり小さい 検定は保守的（conservative）であり，検出力が悪くなると考えられる．よって，5％を超えず，かなり近い 検定が望ましい．
  　なお，1％検定の近似のよさをみるためには N をもう一桁増やし，N = 100000 とした方がよい．
  　結果をみると，このケース（成功確率が真ん中辺でサンプルサイズも比較的大きい）では，連続性の補正 は必要ないと思われる．

  # 連続性補正の効果の R スクリプト

  N <- 10000	# シミュレーション回数
  m <- 30	# n = 30
  y <- NULL	#
  for(i in 1:N){	#
  x <- rbinom(2, m, p=0.4)	# n = 30，p = 0.4 の二項乱数を２回発生
  if(sum(x)==0 || sum(x)==2*m)	# 成功回数が両方とも 0 のとき
  xx <- matrix(c(x[1]+0.5,m-x[1]+0.5,x[2]+0.5,m-x[2]+0.5), nc=2, byrow=T)	# セルすべてに 0.5 を加える
  else	#
  xx <- matrix(c(x[1],m-x[1],x[2],m-x[2]), nc=2, byrow=T)	# 行列化
  y1 <-chisq.test(xx, correct=F)$statistic	# 連続性補正なし χ2 値
  y2 <- chisq.test(xx)$statistic	# 連続性補正 χ2 値
  y <- rbind(y, c(y1, y2))	#
  }	# シミュレーション終わり
  my <- ceiling(max(y))	# χ2 値の最大値を超えない最小の整数
  op <- par(mfrow = c(2, 1))	# 縦２つのグラフ
  y0 <- y[,1]	#
  hist(y0, breaks=seq(0,my,by=0.5),freq=FALSE,xlim=c(0,6),xlab="χ2 値",ylab="頻度",main="")
  x <- seq(0,6, by=0.1)	#
  curve(dchisq(x, 1), 0, 6, add=T, col=2)	# 自由度 1 のし χ2 分布
  title(main="連続性補正なしχ2 値の分布（n = 30）")	#
  q0 <- qchisq(0.95,df=1)	# 自由度 1 の χ2 分布 95％点
  pv <- length(y0[y0>q0])/N	# q0 を超えた頻度（第１種の過誤）
  s <- paste("有意水準 = ", pv)	#
  text(3.5,0.8, s)	#
  segments(q0,0, q0,0.2, col="red")	#
  y0 <- y[,2]	#
  hist(y0, breaks=seq(0,my,by=0.5),freq=FALSE,xlim=c(0,6),xlab="χ2 値",ylab="頻度",main="")
  x <- seq(0,6, by=0.1)	#
  curve(dchisq(x, 1), 0, 6, add=T, col=2)	#
  title(main="連続性補正χ2 値の分布（n = 30）")	#
  q0 <- qchisq(0.95,df=1)	#
  pv <- length(y0[y0>q0])/N	#
  s <- paste("有意水準 = ", pv)	#
  text(3.5,0.8, s)	#
  segments(q0,0, q0,0.2, col="red")	#
  par(op)	#

  
  課題： n = 10 回の試行のときの連続性補正の効果を調べよ．また，成功確率が比較的小さい，たとえば，p = 0.1，のときの 連続性補正の効果を調べよ．このような時は，n = 50 ぐらいは必要だろう．

Fisher の直接確率法

将棋と囲碁 2 × 2 分割表

	勝　ち	負　け	計	場合の数
将　棋	7	3	10	10C7
囲　碁	4	6	10	10C4
計	11	9	20	20C11

パターン１ 勝ち 負け 計   場合の数 将　棋 8  2  10    10C6 囲　碁 3  7  10    10C5 計   11  9  20    20C11   確　率  10C8×10C3 /20C11 = 0.03215		パターン２ 勝ち 負け 計   場合の数 将　棋 9  1  10    10C9 囲　碁 2  8  10    10C2 計   11  9  20    20C11   確　率  10C9×10C2 /20C11 = 0.00268		パターン３ 勝ち 負け 計   場合の数 将　棋 10  0  10    10C10 囲　碁 1  9  10    10C1 計   11  9  20    20C11   確　率  10C10×10C1 /20C11 = 0.00006
パターン４ 勝ち 負け 計   場合の数 将　棋 6  4  10    10C6 囲　碁 5  5  10    10C5 計   11  9  20    20C11   確　率  10C6×10C5 /20C11 = 0.315075		パターン５ 勝ち 負け 計   場合の数 将　棋 5  5  10    10C5 囲　碁 6  4  10    10C6 計   11  9  20    20C11   確　率  10C5×10C6 /20C11 = 0.315075		パターン６ 勝ち 負け 計   場合の数 将　棋 4  6  10    10C4 囲　碁 7  3  10    10C7 計   11  9  20    20C11   確　率  10C4×10C7 /20C11 = 0.15004
パターン７ 勝ち 負け 計   場合の数 将　棋 3  7  10    10C3 囲　碁 8  2  10    10C8 計   11  9  20    20C11   確　率  10C3×10C8 /20C11 = 0.03215		パターン８ 勝ち 負け 計   場合の数 将　棋 2  8  10    10C2 囲　碁 9  1  10    10C9 計   11  9  20    20C11   確　率  10C2×10C9 /20C11 = 0.00268		パターン９ 勝ち 負け 計   場合の数 将　棋 1  9  10    10C1 囲　碁 10  0  10    10C10 計   11  9  20    20C11   確　率  10C1×10C10 /20C11 = 0.00006

• 勝率同等性の Fisher 直接確率法検定
  

  # 勝率同等性　Fisher 直接法の R スクリプト

  shogi <- c(7, 3)	# A の将棋の勝ち負け数
  igo <- c(4, 6)	# A の囲碁の勝ち負け数
  x <- rbind(shogi, igo)	# 行連結による行列化
  fisher.test(x)	# 勝率同等性 Fisher 直接確率

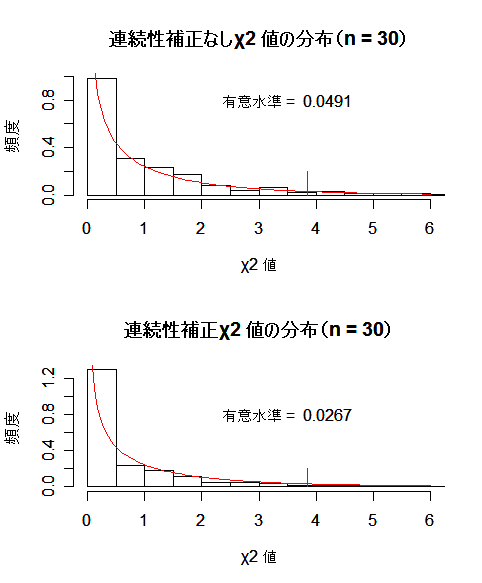
  課題： 勝敗の比率はそのままで，試行回数を増やして（n = 30）同様な検定を行え．

クロス集計と独立性の検定

2 × 2 分割表データ

	反応１	反応２	計
集団１	n11	n12	n1・
集団２	n21	n22	n2・
計	n・1	n・2	n

　ここで，n_ij は，集団 i の標本の中で，反応 j を取った人数（度数） である．また，n_i・ は集団 i の標本の大きさで， n_・j は標本全体（大きさ n）の中で反応 j を取った人数 を表し，それぞれ周辺度数という．
　このような表において，集団で反応パターンに違いがなければ，集団 i で反応 j を取る確率は， 集団 i である確率 n_i・/n に 集団 j である確率 n_・j/n をかけた n_i・n_・j/ n² となることが期待される．これより， 集団 i で反応 j を取る人数（度数）は， n_i・n_・j/n となることが期待される．これを独立性の仮定という．
　いま，集団 i の標本の中で，反応 j を取る確率を p_ij とし，集団 i の周辺確率を p_i.， 反応 j の周辺確率を p_.j とすると，独立性の仮説は，

φ（ファイ）係数

のようにまとめられる．φ 係数は，この 2 つの変数間のピアソン相関係数である． すなわち，「将棋」と「勝ち」の相関である．
　多少の計算により，ピアソン χ² 値との関係は，

# φ 係数の R スクリプト

a <- c(rep(1, 10), rep(0, 10)) # 「将棋」の値 b <- c(rep(1, 7), rep(0, 3), rep(1, 4), rep(0, 6)) #「勝ち」の値 cor(a, b) # φ 係数（a，b 間の相関係数） n <- length(a) shogi <- c(7, 3) # A の将棋の勝ち負け数 igo <- c(4, 6) # A の囲碁の勝ち負け数 　 x <- rbind(shogi, igo) c2 <- chisq.test(x, correct=F)$statistic # ピアソン χ2 値（連続性補正なし） sqrt(c2/n) # φ 係数

オッズ比（odds ratio）

• 食中毒原因食材の χ² 独立性検定とオッズ比
  　1940 年のNew York 州Oswego の協会の夕食会における胃腸炎異常発生の喫食 調査データによる．ケーキと食中毒症状とで以下の関係があった．これより， ケーキが食中毒の原因食材と考えられるか検討できる．

  	発症あり	発症なし
  食べた	27	13
  食べなかった	19	16

  # 食材と中毒症状 χ² 検定の R スクリプト

  x <- matrix(c(27, 13, 19, 16), nc=2, byrow=T)	# ケーキと中毒症状の関係データ
  x[1,1]*x[2,2]/(x[2,1]*x[1,2])	# オッズ比の単純な推定値
  chisq.test(x)	# 独立性 χ2 検定
  fisher.test(x)	# 独立性 Fisher 直接確率法

  課題：ケーキの他の食材ののデータの一部は以下の表のようであった．このデータから， 食中毒の原因食材を推定せよ．

  食品名	発症あり		発症なし
  	食べた	食べない	食べた	食べない
  ハムステーキ	29	17	17	12
  バニラアイス	43	3	11	18
  チョコアイス	25	20	22	7
  フルーツサラダ	4	42	2	27

シンプソンのパラドックス

賛成 反対  計   男  132 67 199 女 93 108 201 計 225 175 400

賛成 反対  計  35 未満 131 67 198 35 以上 94 108 202 計 225 175 400

　これをみると，男性は約 2/3 が賛成してあり，年齢別では 35 未満の賛成も約 2/3 であった． この結果をみると，若い男性がこの政策に賛成していると考えがちである．しかし，性別，年齢別に細かく 集計してみると，

賛成 反対  計  男 35 未満 41 58 99 男 35 以上 91 9 100 計 132 67 199

賛成 反対  計  女 35 未満 90 9 99 女 35 以上 3 99 102 計 93 108 201

となり，35 歳未満の男性の反対がけっこう多く，予想とは異なる結果となった．このようになった理由は，35 歳 以上の男女で賛否がまったく異なっていて，さらに女性でも 35 歳未満と以上で賛否がまったく異なって いたからである．このような状況を無視して，年齢層でひとくくりにしたり，性別でひとくくりしたことが 誤った推論を引き起こす原因となったと考えられる．
　このように，まったく異なった性格を持つ集団をまとめてしまってデータの解釈を行うことは危険である． したがって，2 元分割表に基づいて分析をするときは，集団の中に層構造が隠れていないかよく調べる 必要がある．

マンテル・ヘンツェル（Mantel-Haenszel）検定

# マンテル・ヘンツェル検定の R スクリプト

Data <- array(c(41, 91, 58, 9, 90, 3, 9, 99), dim = c(2, 2, 2), dimnames = list( 年齢 = c("35 未満", "35 以上"), 賛否 = c("賛成", "反対"), 性別 = c("男性", "女性"))) Data mantelhaen.test(Data)

マクネマー（McNemar）検定

H₀：1 回目と 2 回目で賛否の比率が変わらない．

• 大統領支持率変化のマクネマー検定
  　R のサンプルデータで紹介されている Agresti (1990) のデータによる．選挙権のある年齢の アメリカ人のランダムサンプル 1,600 名の 1 か月での大統領の支持率の変化が以下の表になった． 大統領の支持率に変化があったかを調べてみよう．

  	支持（2 回目）	不支持（2 回目）
  支持（1 回目）	794	150
  不支持（1 回目）	86	570

  # マクネマー検定の R スクリプト

  Performance <- matrix(c(794, 86, 150, 570), nrow = 2, dimnames = list("1 回目調査" = c("支持", "不支持"), "2 回目調査" = c("支持", "不支持"))) Performance mcnemar.test(Performance) # 適切な検定 chisq.test(Performance) # 適切でない検定

R × C 表

R × C 分割表データ

	B1	B2	…	BC	計
A1	n11	n12	…	n1C	n1・
A2	n21	n22	…	n2C	n2・
：	：	：	…	：	：
AR	nR1	nR2	…	nRC	nR・
計	n・1	n・2	…	n.C	n

すると，2 × 2 分割表のときと同様に， 集団 i の標本の中で，反応 j を取る確率を p_ij とし，集団 i の周辺確率を p_i.， 反応 j の周辺確率を p_.j とすると，独立性の仮説は，

• カップヌードルの好みと年代との関連の χ² 検定
  　カップヌードルの好みは年代によって違いがあるかどうかを調べた．10 代，20 代，30 代，40 代 の被験者をそれぞれ 100 名ずつ選び，好みを聞いたところ以下の表がえられたとしよう（仮想データ）．
  
  帰無仮説 H₀：ヌードルの好みは年代により異ならない
  の検定を行ってみる．

  年代による好みの違い

  	10 代	20 代	30 代	40 代	計
  カップヌードル	41	50	57	56	204
  シーフードヌードル	59	50	43	44	196
  計	100	100	100	100	400

  グラフに図示すると以下のようになった． 若い人（10 代）はシーフードヌードルを好み， 比較的年配の人（30 代，40 代）はカップヌードルを好む傾向にありそうに見える．
  

  # カップヌードルの好みの R スクリプト

  cup <- c(41, 50, 57, 56) # カップヌードルが好き，年代別データ sea <- c(59, 50, 43, 44) # シーフードヌードルが好き，年代別データ x <- rbind(cup, sea); x chisq.test(x) # χ2 検定

  課題： 30 代と 40 代では，好みに違いがなさそうなので，検定の自由度を減らすため，30 代と 40 代でまとめて， 10 代，20 代，30・40 代の 3 つのカテゴリーにまとめて検定を行なえ．

２．分散分析

因子と水準

一元配置（one-way layout）

構造モデル

平方和分解

平方和の期待値

帰無仮説のもとでの平方和の比の分布

分散分析表と F 検定

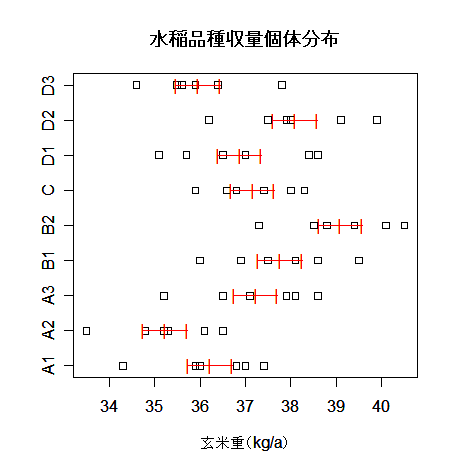
• 品種によるコメの収量の違い
  水稲の９品種をそれぞれ，６区画の水田で栽培したときのアール当たりの玄米重量は以下のようであった． このうち，A，B，D，それぞれ，同じ母本から育成された品種であり，C は標準（対照 control）品種である．
  このデータは一元配置分散分析で解析できる．処理が品種で，9 水準からなっている．帰無仮説は，
  H₀：収量はどの品種も同じである
  である．

  データダウンロード

  # 水稲品種収量分散分析の R スクリプト

  yy <- read.csv("hinsyu.csv"); yy	# csv データ読み込み
  n <- nrow(yy)	# 繰り返し数
  a <- ncol(yy)	# 処理数
  y <- NULL; x <- NULL	#
  for(i in 1:a){	#
  x <- c(x, rep(i, n))	# 品種番号ベクトル
  y <- c(y, yy[,i])	# 収量データベクトル
  }	#
  x <- factor(x)	# ラベル化
  cbind(y,x)	# ベクトルデータ表示
  summary(aov(y ~ x))	# 一元配置分散分析
  anova(lm(y ~ x))	# 一元配置分散分析（これでもよい）
  # 分散分析の計算を以下で詳しくみる
  nn <- length(y)	# 総データ数
  s <- diag(var(yy)*(n-1))	# 各品種内誤差
  se <- sum(s); se	# 誤差平方和
  st <- var(y)*(nn-1)	# 総平方和
  sa <- st - se; sa	# 処理平方和
  va <- sa/(a - 1); va	# 処理平均平方
  ve <- se/(nn - a); ve	# 誤差平均平方
  fv <- va/ve; fv	# F 値
  pv <- 1 - pf(fv, df1=(a-1), df2=(nn-a)); pv	# p 値
  # データの品種ごとのちらばりと，品種平均と標準誤差を視覚化する
  xm <- 1:9	#
  ym <- mean(yy)	# 品種ごとの平均
  vm <- ve/n	# 品種平均の分散
  svm <- sqrt(vm)	# 品種平均の標準誤差
  stripchart(yy, xlab="玄米重（kg/a）")	# 品種ごとの個体分布表示
  text(ym, xm,"|", col="red")	# 品種平均
  text(ym+svm, xm,"|", col="red")	# 品種平均 ＋ 標準誤差
  text(ym-svm, xm,"|", col="red")	# 品種平均 − 標準誤差
  segments(ym-svm, xm, ym+svm, xm, col="red")	# 横線
  title(main="水稲品種収量個体分布")	#

  　水稲収量データの分散分析表は以下のようになり，品種の効果は有意確率 0.001（0.1 ％）以下の *** で， 強度に有意となった．

  水稲収量分散分析表

  変動因	自由度（df）	平方和（SS）	平均平方（MS）	F 値
  主効果	8	66.17	8.27	5.99 ***
  誤　差	45	62.09	1.38
  全　体	53	128.26

  　また，各品種ごとの個体分布を図示すると以下のようになった．
  

対比（contarst）

　対比 C = Σ_ic_iμ_i は C^{^} = Σ_ic_iX^-_i. で推定されるが， 帰無仮説（α_i = 0）のもとでは， 対比推定量の平均と分散は，

　ところで，別の対比 Σ_id_iμ_i があったときに， Σ_ic_i d_i = 0，となるものを直交対比という． 直交対比の組は同時に検定ができる． 　事前に比較が決められるときは，後述する多重比較による有意確率の補正を行わないことが多いと思われる．

• 母本による収量の違い（対比）
  　前節では，すべての品種間で差がないかどうかの検定を行った．その結果，すべての品種の収量が同じという 帰無仮説は強度に有意で棄却された．ここで，母本により収量に違いがあるかを見てみよう． いま，母本 A と B の 違いに注目しているとしよう．これは，
  
  で表されるが，このときの対比の係数は，
  c₁ = (1/3, 1/3, 1/3, -1/2, -1/2, 0, 0, 0, 0)
  である．この対比に直交するものとしては，例えば，標準品種 C と母本 D との間の違い，
  
  が考えられる．この対比の係数は，
  c₂ = (0, 0, 0, 0, 0, 1, -1/3, -1/3, -1/3)
  であり，c₁ と c₂ の 内積 c₁'c₂ = 0 なので， c₁ と c₂ は直交していることがわかる．

  　対比の検定の結果，母本 A と B の差は強度に有意（0.1％以下）であり，母本 A からの系統 の方が収量が高いと言える．また，標準品種 C と母本 D の系統では，有意な差が認められなかった．

  # 母本による収量差の対比の R スクリプト

  c1 <- c(1/3,1/3,1/3,-1/2,-1/2, 0, 0, 0, 0)	# 母本 A と B の平均の差の対比係数ベクトル
  c2 <- c(0, 0, 0, 0, 0, 1,-1/3,-1/3,-1/3)	# 標準品種 C と母本 D の平均の差の対比係数ベクトル
  contrasts(x) <- cbind(c1, c2)	# 品種ラベルに対比を定義する．
  contrasts(x)	# 定義した残りの直交対比は R が勝手につくる
  fc <- lm(y ~ x)	# 対比つき線形モデル
  summary(fc)	# 結果表示（最初の２つの対比のみに着目）
  # 対比の計算を詳しくみる
  gm <- tapply(y, x, mean); gm	# 品種平均
  cmat <- contrasts(x)[,1:2]	# 対比係数ベクトルの必要部分
  mc <- diag(t(cmat) %*% cmat)	# 対比係数ベクトルの長さの２乗
  esd <- summary(fc)$sigma	# 誤差標準偏差の推定値
  csd <- sqrt(mc)*esd/sqrt(n)	# 対比の標準誤差
  ce <- t(cmat) %*% gm	# 対比推定値（母本平均の差）
  tv <- ce/csd; tv	# 対比 t 値
  2*(1 - pt(abs(tv), df=(nn-a)))	# 対比 p 値
  ce <- ce/mc; ce	# 対比係数ベクトルの長さで補正した対比推定値
  csd <- csd/mc; csd	# 対比係数ベクトルの長さで補正した対比標準誤差

多重比較（multiple comparison）

　前節の対比でも，考えられる対比を無原則に行うときは多重比較の問題を考慮しなければならないが，この節 では対比の中でも最も単純な対比較（pairwise comparison），すなわち， 個々の処理水準間の比較のみを取り上げる．
　いま，処理平均 μ_i と μ_j の比較を行う場合を考える． 2 つの処理平均の差 μ_i - μ_j は， d_ij = X^-_i. - X^-_j. で推定される． 帰無仮説（α_i = α_j = 0）のもとで，d_ij の平均と分散は，

• なにもしない
  推奨されない方法である．すなわち，補正なしの t 検定を行う．昔の LSD である．
  R では，|d_ij| の p 値が出力 される．
• ボンフェローニ（Bonferroni）補正
  いま，有意水準 α' のそれぞれ独立な検定を r 回行ったとすると，1 回の検定で正しい判断を行う確率が 1 - α' なので，r 回の検定で正しい判断を行う確率は，(1 - α')^r となる．よって，正しい判断 を行わない（第 1 種の過誤の）確率は，
  1 - (1 - α')^r ≒ 1 - (1 - rα') = rα'，ただし，α' ≒ 0
  となる．これが，r 回の検定全体での有意水準となる．よって，検定全体での有意水準を α にするには， 1 回の検定の有意水準を α' = α/r にすればよい．これがボンフェローニ補正である．しかし， 多重比較における検定は独立な検定ではないので，この補正は厳しすぎ（保守的）て， 有意な組み合わせが見つからない恐れがある．
  R の多重比較では，補正なしの p 値を r 倍した p 値を出力する．ただし，これが 1 を超えた場合は 1 とする．
• ホルム（Holm）補正
  ボンフェローニ補正を改良したものである．すべての比較組み合わせ（対比）の t 値を計算し， それを大きさの順に並べる．一番大きな t 値 t₍₁₎ の有意確率を α/r，次の大きさ の t₍₂₎ の有意確率を α/(r - 1)，というように有意確率を調整する．
  R ではホルム補正がデフォルトで， p 値を大きさの順に並べ最も小さな p 値を r 倍し，次に大きな p 値を r - 1 倍して出力するようである．

  # コメ収量多重比較の R スクリプト

  pth <- pairwise.t.test(y, x); pth	# 対比較ホルム補正
  ptb <- pairwise.t.test(y, x, p.adj = "bonf"); ptb	# 対比較ボンフェローニ補正
  ptn <- pairwise.t.test(y, x, p.adj = "none"); ptn	# 対比較補正なし
  showpt.f <- function(x, p){	# p 値が p 以下の比較を表示する関数
  pl <- which(x < p, arr.ind=TRUE)	# 行列 x の要素が p 以下の場所
  cbind(pl[,2], x[pl])	# 場所と p 値の表示
  }	#
  showpt.f(pth$p.value, 0.05)	# 対比較ホルム補正で 5 ％有意となった比較
  showpt.f(ptb$p.value, 0.05)	# 対比較ボンフェローニ補正で 5 ％有意となった比較
  showpt.f(ptn$p.value, 0.05)	# 対比較補正なしで 5 ％有意となった比較
  # 多重比較の計算を詳しくみる（品種１と５の比較）
  c15 <- c(1,0,0,0,-1,0,0,0,0)	# 対比ベクトル
  mc15 <- c15 %*% c15	# 大きさ
  c15sd <- sqrt(mc15)*esd/sqrt(n)	# 対比較の標準誤差
  c15e <- t(c15) %*% gm	# 対比較推定値
  tv15 <- c15e/c15sd; tv15	# 対比較 t 値
  pv15 <- 2*(1 - pt(abs(tv15), df=(nn-a)));pv15	# 対比較 p 値
  k <- a*(a-1)/2	# 比較の総数
  pv15*k	# 対比較 p 値ボンフェローニ補正

• チューキー（Tukey）の HSD（honestly significant difference）
  今までは，t 検定の有意確率を補正することにより，多重比較の問題に対処していたが， スチィーデント化された範囲の分布 （Studentized range distribution）という多重比較専用の分布 を用いて検定する．2 つの処理 i，j 間の比較 を行うときに用いる検定統計量は，先ほどの t_ij である．

  # コメ収量 Tukey HSD の R スクリプト

  hsd <- TukeyHSD(aov(y ~ x)); hsd	# チューキー HSD のすべての組み合わせの結果表示
  ph <- hsd$x[,4]	# 各比較の p 値ベクトル
  sc <- (1:length(ph))[ph<0.05]	# p 値が 0.05 以下の比較
  hsd$x[sc,]	# 5 ％有意な比較

• 多重比較法による結果
  コメ９品種収量の多重比較を行った結果 5 ％有意となった組み合わせは以下の表にまとめられる．有意 確率の補正とチューキー HSD は似た結果を与えたが，補正なしの LSD では倍以上の組み合わせが有意 とされた．

  多重比較法	共通の組み合わせ	補正なしと HSD	補正なし
  ホルム補正	1-5 2-4 2-5 2-8 5-9
  ボンフェローニ補正
  補正なし		5-7	1-4 1-8 2-3 2-6 2-7 3-5 4-9 5-6 8-9
  チューキー HSD

• 多重比較法の比較
  多重比較の方法はここで取り上げた以外の手法も知られているが，R で手軽に使える手法を解説した． ここで紹介した手法の有意水準をシミュレーションで比較してみる．標準正規乱数 50 を 1 から 5 まで のグループに 10 個ずつ分ける．このデータを処理数 a = 5，処理内標本 n = 10 の一元配置データ とみなす．このデータは帰無仮説が真のときで，処理平均に差がないはずである．
  　分散分析 F 検定の p 値とホルム補正，ボンフェローニ補正，補正なし，チューキー HSD の 多重比較の p 値の最小値 を出す．p 値の最小値が 0.05 以下であれば，5 ％有意な組み合わせが少なくとも 1 つは存在 したことになる．これを，N = 10000 回繰り返して有意な組み合わせが見つかった回数を調べれば 有意水準がわかる．

  　その結果は以下の表のようになった．また，分散分析の F 検定で有意になったときと そうでないときで多重比較で有意な組み合わせが見つかったかどうかも分類した．これをみると， 補正なしの多重比較は有意水準 25 ％以上で， 明らかにゴーストを拾ってしまうことがわかり，これを使ってはいけないことが 示された．
  　一方，ホルム補正とボンフェローニ補正は，このシミュレーションでは違いがまったくなかった． これは，p 値の最小値の補正はどちらも α/r であるからである． 有意水準が 4 ％ぐらいであり，問題がないと言える．チューキー HSD の有意水準は約 5 ％ で一番よいと言える．
  　また，分散分析 F 検定との関連をみると，多重比較の有意な組み合わせの有無は F 検定と 大きく関連があると言えるが，まったく一致しているわけではなかった．分散分析 F 検定と多重比較は 違う検定と考えた方がよいと思われる．すなわち，分散分析 F 検定が有意なときだけ多重比較を行うと 有意水準が低下するので，より保守的な検定になってしまうからである．

  多重比較法の有意水準と F 検定の有意性との関係

  	F 検定	ホルム補正	ボンフェローニ補正	補正なし	チューキー HSD
  有意水準	0.0497	0.0377	0.0377	0.2807	0.0503
  有意となった組み合わせ があった回数	有意なとき（497）	337	337	497	393
  	有意でないとき	40	40	2310	110

  # 多重比較法の有意水準 の R スクリプト

  N <- 1000	# シミュレーション回数（時間節約のため減らした）
  a <- 5; n <- 10	# 処理水準数 a，処理内標本数 n
  x <- NULL	#
  for(i in 1:a) x <- c(x, rep(i, n))	# グループラベル
  x <- factor(x)	# ラベル化
  pv <- NULL	# p 値行列
  for(i in 1:N){	#
  y <- rnorm(n*a)	# 標準正規乱数 n*a 個
  pth <- pairwise.t.test(y, x)	# 対比較ホルム補正
  ptb <- pairwise.t.test(y, x, p.adj = "bonf")	# 対比較ボンフェローニ補正
  ptn <- pairwise.t.test(y, x, p.adj = "none")	# 対比較補正なし
  av <- aov(y ~ x)	# 分散分析
  hsd <- TukeyHSD(av)	# チューキー HSD
  p0 <- summary(av)[[1]][1,5]	# 分散分析 p 値
  p1 <- min(pth$p.value, na.rm=TRUE)	# 対比較ホルム補正の p 値の最小値
  p2 <- min(ptb$p.value, na.rm=TRUE)	# 対比較ボンフェローニ補正の p 値の最小値
  p3 <- min(ptn$p.value, na.rm=TRUE)	# 対比較補正なしの p 値の最小値
  p4 <- min(hsd$x[,4])	# チューキー HSD の p 値の最小値
  pv <- rbind(pv, c(p0, p1,p2,p3,p4))	# p 値行列に格納
  }	#
  fs <- (1:N)[pv[,1]<0.05]	# 分散分析で 5 ％有意となった回の番号
  hs <- (1:N)[pv[,2]<0.05]	# 対比較ホルム補正で 5 ％有意な組み合わせがあった回の番号
  bs <- (1:N)[pv[,3]<0.05]	# 対比較ボンフェローニ補正で 5 ％有意な組み合わせがあった回の番号
  ns <- (1:N)[pv[,4]<0.05]	# 対比較補正なしで 5 ％有意な組み合わせがあった回の番号
  ts <- (1:N)[pv[,5]<0.05]	# チューキー HSD で 5 ％有意な組み合わせがあった回の番号
  num <- c(length(fs), length(hs), length(bs), length(ns), length(ts))
  num/N	# 有意水準
  table(hs %in% fs)	# 対比較ホルム補正の番号と分散分析有意の番号とのマッチング
  table(bs %in% fs)	# 対比較ボンフェローニ補正の番号と分散分析有意の番号とのマッチング
  table(ns %in% fs)	# 対比較補正なしの番号と分散分析有意の番号とのマッチング
  table(ts %in% fs)	# チューキー HSD の番号と分散分析有意の番号とのマッチング

二元配置（two-way layout）

構造モデル

各種平方和

分散分析表と F 検定

実験計画法

実験計画法（追加）

# コメ収量データ の R スクリプト

rice <- read.csv("ricecul.csv")	# コメデータ読み込み
rice[rice$year==2000,]	# 2000年度データの表示
yield0 <- rice$gy[rice$year==2000]	# 2000年度収量
dens0 <- factor(rice$density[rice$year==2000])	# 2000年度密度水準のラベル化
fert0 <- factor(rice$fert[rice$year==2000])	# 2000年度肥料水準のラベル化
blk0 <- factor(rice$rep[rice$year==2000])	# 2000年度ブロックのラベル化
cbind(yield0, dens0, fert0, blk0)	# データと変数の表示
ry.aov <- aov(yield0 ~ blk0 + dens0 + fert0 + dens0:fert0)	# ２要因乱塊法分散分析
summary(ry.aov)	# 分散分析表表示
x <- tapply(yield0, dens0:fert0, mean); x	# 栽植密度と施肥量組み合わせの収量平均
plot(1:3, x[1:3], type="b", lwd=2, xaxt="n", xlab="施肥量", ylab="収量", ylim=c(300, 600), pch=0, col="blue")
axis(1, 1:3, labels=c("施肥無","施肥少","施肥多"))	# グラフ表示
points(1:3, x[4:6], type="b", lwd=2, pch=2, col="red")	#
legend(locator(1), legend=c("疎植","密植"), pch=c(0,2), col=c("blue","red"))
title(main="栽植密度と施肥量の交互作用（2000年）")	#

課題：収量の他の年度の分散分析を行え．

# コメ収量年次効果の R スクリプト

yield <- rice$gy	# コメ収量データ
dens <- factor(rice$density)	# 密度水準のラベル化
fert <- factor(rice$fert)	# 施肥量水準のラベル化
year <- factor(rice$year)	# 年次のラベル化
cbind(yield, dens, fert, year)	# データと変数の表示
rya.aov <- aov(yield ~ dens + fert + year + dens:fert + fert:year + dens:year + dens:fert:year)
summary(rya.aov)	# ３元配置分散分析表
x <- tapply(rice$gy, fert:year, mean)	# 年次と施肥量組み合わせの収量平均
plot(1:4, x[1:4], type="b", lwd=2, xaxt="n", xlab="年次", ylab="収量", ylim=c(300,600), pch=0, lty=1,col="red")
axis(1, 1:4, labels=levels(year))	# グラフ表示
points(1:4, x[5:8], type="b", lwd=2, pch=2,lty=1, col="blue")	#
points(1:4, x[9:12], type="b", lwd=2, pch=3,lty=1, col="green")	#
legend(locator(1), legend=c("施肥無","施肥少","施肥多"), pch=c(0,2,3), col=c("red","blue","green"))
title(main="年次と施肥量の交互作用")	#

課題：他の形質の分散分析を行え．

参考文献

1. 心理・教育のための統計法（第 2 版），山内光哉，1998，サイエンス社
2. 工学のためのデータサイエンス入門−フリーな統計環境Rを用いたデータ解析−，間瀬茂ら，2004， 数理工学社
3. 実践生物統計学−分子から生態まで−（第 1 章，第 2 章）， 東京大学生物測定学研究室編（大森宏ら）， 2004，朝倉書店
4. R で学ぶデータマインニング I −データ解析の視点から−，熊谷悦生・船尾暢男，2007，九天社
5. R で学ぶデータマインニング II −シミュレーションの視点から−，熊谷悦生・船尾暢男，2007，九天社
6. 生物統計学入門，上村賢治・高野泰・大森宏，2008，オーム社