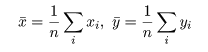
標本(サンプル)に対し,2つの変数 x,y が測定されているとする. たとえば,x が身長(m)であり,y が体重(kg)である. 大きさ n の標本(サンプル)に対し,2つの変数の組のデータが,
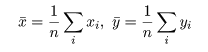
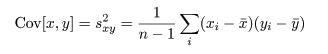
共分散は測定単位により大きさが変わるので,これをおのおのの変数の標本分散, Var[x],Var[y],
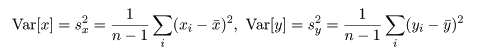
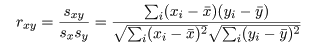
 |
 |
 |
 |
| r <- read.csv("r1.csv") | # csv データ読み込み |
| x <- r[,1]; y <- r[,2] | # |
| plot(x,y, xlim=c(2,8), ylim=c(0,6)) | # x,y の散布図 |
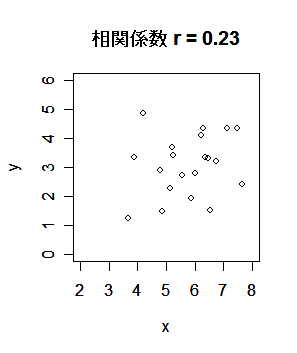
| title(main="相関係数 r = 0.23") | # |
| cov(x, y) | # x と y の共分散 |
| cor(x, y) | # x と y の相関係数 |
| x <- 10*x | # |
| plot(x,y, xlim=c(2,8), ylim=c(0,6)) | # x,y の散布図 |
| cov(x, y) | # x と y の共分散 |
| cor(x, y) | # x と y の相関係数 |
| library(MASS) | # MASS ライブラリーの読み込み |
| s <- matrix(c(100, 70, 70, 100), nrow=2) | # 分散共分散行列の定義 |
| x <- mvrnorm(1000,c(50,50),s) | # 平均 50,分散 s の 2 変量正規分布乱数 1000 個生成 |
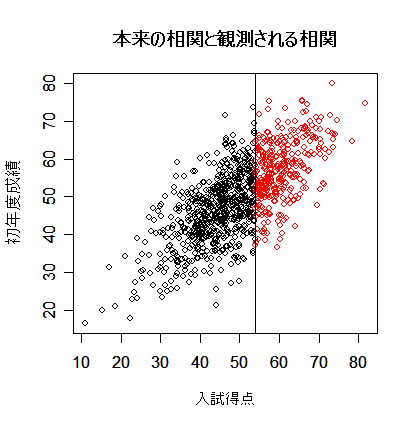
| plot(x, xlab="入試得点", ylab="初年度成績") | # 分布全体を表示 |
| points(x[x[,1]>54,], col="red") | # 入学者のみ赤で表示 |
| abline(v=54) | # 合格ライン |
| title(main="本来の相関と観測される相関") | # |
| cor(x)[1,2] | # 本来あるべき相関 |
| cor(x[x[,1]>54,])[1,2] | # 実際に観測される相関 |
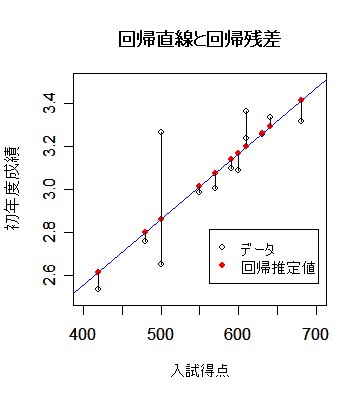
データに最もよくあてはまる直線回帰式を得るには,データ点 (xi ,yi ), と回帰による推定点, (xi ,y^i ), y^i = a + b xi , の間の距離の2乗和 S が最小になるような回帰係数 a ,b を求める.つまり,
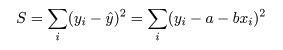
これは,S を a ,b で偏微分して 0 とおくことによって得られる.つまり,
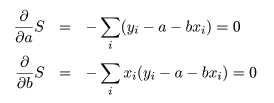
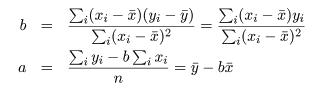
| 入試得点(x) | 680 | 500 | 600 | 420 | 480 | 630 | 550 | 590 | 610 | 500 | 640 | 570 | 610 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 初年度成績(y) | 332 | 265 | 309 | 253 | 276 | 326 | 299 | 310 | 324 | 327 | 334 | 301 | 336 |
| mba <- read.csv("mbagrade2.csv") | # データ読み込み |
| mbaf <- mba[mba[,1]=="F",] | # 女性データのみ抽出 |
| mbaf.lm <- lm(初年度成績 ~ 入試得点, data=mbaf) | # 回帰:lm(y ~ x, data=zzz), y = ax + b |
| summary(mbaf.lm) | # 結果表示 |
| plot(mbaf[,2:3], xlim=c(400,700), ylim=c(2.5,3.5)) | # データ散布図 |
| abline(mbaf.lm, col="blue") | # 回帰直線 |
| points(mbaf[,2], mbaf.lm$fitted.value, pch=19, col="red") | # 回帰推定値 |
| segments(mbaf[,2],mbaf[,3],mbaf[,2], mbaf.lm$fitted.value) | # 回帰残差 |
| title(main="回帰直線と回帰残差") | # |
| legend(locator(1), legend=c("データ","回帰推定値"), pch=c(1,19), col=c("black","red")) | |
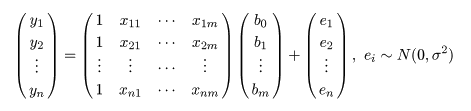
推定された直線回帰式がどの程度現実のデータに適合しているかを調べるために, 回帰式が従う統計モデルを考える.標本の格データ点, (xi ,yi ), が,
回帰で説明がつかない残差平方和 Se は,
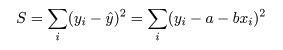
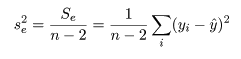
一般に,Var(yi ) = σ2 であるとき,その定数 倍の分散は,
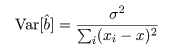
目的変数 y が説明変数 x との回帰関係にないという 帰無仮説,
回帰係数 b の推定値 b^ の分散は,
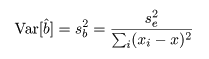
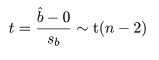
回帰式により, 従属変数 y のデータ yi は,
データが直線回帰式でよく説明できるのは,回帰平方和が大きく,残差平方和 が小さい場合である.総平方和のうち回帰平方和で説明される割合を決定係数,もしくは 重相関係数の2乗といい,
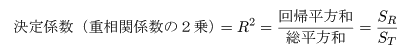
| 変動因 | 平方和 | 自由度 | 平均平方 | F 値 |
|---|---|---|---|---|
| 回帰 | SR | 1 | SR | F = SR/se2 |
| 残差 | Se | n−2 | se2 = Se/n−2 | |
| 全体 | ST | n−1 |
従属変数 y が説明変数 x の回帰関係にないという 帰無仮説,
| anova(mbaf.lm) | # 分散分析表 |
| n <- nrow(mbaf); n | # データ数 |
| st <- var(mbaf[,3])*(n-1); st | # 総平方和 |
| sr <- var(mbaf.lm$fitted.values)*(n-1); sr | # 回帰平方和 |
| se <- var(mbaf.lm$residuals)*(n-1); se | # 残差平方和 |
| s <- sqrt(se/(n-2)); s | # 残差標準偏差 |
| sx <- var(mbaf[,2])*(n-1); sx | # x の総平方和 |
| b <- cov(mbaf[,2],mbaf[,3])*(n-1)/sx; b | # 回帰係数 |
| sb <- s/sqrt(sx); sb | # 回帰係数bの標準誤差 |
| r2 <- sr/st; r2 | # 重相関係数の2乗 |
| r <- cor(mbaf[,3], mbaf.lm$fitted.values); r | # 目的変数と回帰推定値の相関 |
| fv <- sr/(se/(n-2)); fv | # F値 |
| tv <- b/sb; tv | # t値 |
回帰係数の標準誤差 s b を用いて, 回帰係数 b の信頼区間がつくれる.すなわち, 自由度 n−2 の t 分布の 97.5%点を t0 とすると, 回帰係数 b の 95%信頼区間の幅 d は,d = t0 s b となるので, 95%信頼区間は,
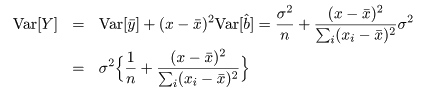
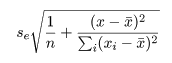
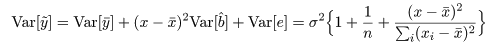
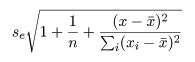
| x <- mbaf[,2] | # 入試得点 |
| y <- mbaf[,3] | # 初年度成績 |
| d <- lm(y ~ x) | # 回帰モデル |
| new <- data.frame(x=seq(400,700,by=2)) | # 予測したい範囲の定義 |
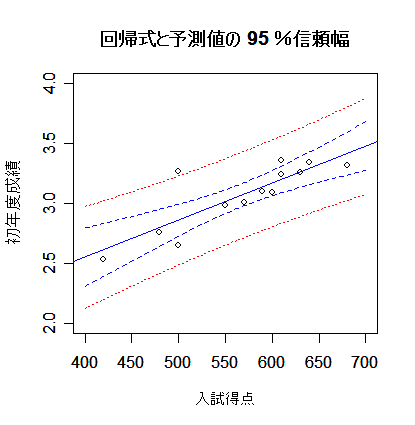
| dc <- predict(d, new, interval="confidence", level=0.95) | # 回帰推定値(回帰直線)の 95 %信頼幅 |
| dp <- predict(d, new, interval="prediction", level=0.95) | # 回帰予測値の 95 %信頼幅 |
| matplot(new$x, cbind(dc,dp[,-1]), lty=c(1,2,2,3,3), type="l", col=c("blue","blue","blue","red","red"), xlab="入試得点", ylab="初年度成績") | |
| points(x, y) | # データの表示 |
| title(main="回帰式と予測値の 95 %信頼幅") | # |
| # 信頼幅を詳しく計算 | |
| n <- nrow(mbaf); n | # データ数 |
| sx <- var(x)*(n-1); sx | # x の偏差平方和 |
| se <- summary(d)$sigma; se | # 残差標準偏差 |
| b <- d$coefficients[2]; b | # 回帰係数 |
| mx <- mean(x) | # x の平均 |
| my <- mean(y) | # y の平均 |
| t0 <- qt(0.975, df=(n-2)); t0 | # 自由度 n - 2 の t 分布 97.5%点 |
| plot(x, y, xlim=c(400,700), ylim=c(2,4)) | # データ散布図 |
| abline(d, col="blue") | # 回帰直線 |
| sr <- 1/n + (new$x-mx)^2/sx | # |
| y1 <- my + b*(new$x-mx) + t0*se*sqrt(sr) | # 回帰直線 95%信頼幅上限 |
| y2 <- my + b*(new$x-mx) - t0*se*sqrt(sr) | # 回帰直線 95%信頼幅下限 |
| points(new$x, y1, type="l", lty=2, col="blue") | # |
| points(new$x, y2, type="l", lty=2, col="blue") | # |
| yp1 <- my + b*(new$x-mx) + t0*se*sqrt(sr+1) | # 回帰予測値 95%信頼幅上限 |
| yp2 <- my + b*(new$x-mx) - t0*se*sqrt(sr+1) | # 回帰予測値 95%信頼幅下限 |
| points(new$x, yp1, type="l", lty=3, col="red") | # |
| points(new$x, yp2, type="l", lty=3, col="red") | # |
| title(main="回帰式と予測値の 95 %信頼幅") | # |
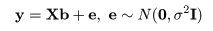
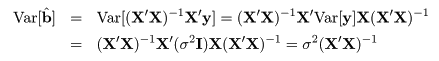
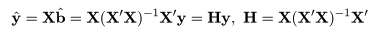
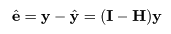
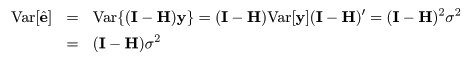
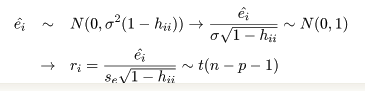
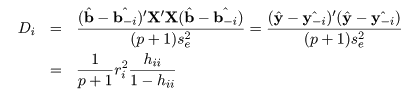
 |
 |
 |
 |
mba <- read.csv("mbagrade2.csv") # データ読み込み
mbaf <- mba[mba[,1]=="F",] # 女性データのみ抽出
mbaf.lm <- lm(初年度成績 ~ 入試得点, data=mbaf) #
summary(mbaf.lm) # 結果表示
plot(mbaf[,2:3], type="n", xlim=c(400,700), ylim=c(2.5,3.5)) # データ散布図
text(mbaf[,2:3], rownames(mbaf)) # データ番号表示
abline(mbaf.lm, col="blue") # 回帰直線
x11() # 新しいグラフウィンドウ
plot(mbaf.lm) # 回帰診断はたったこれだけ.(4枚のグラフが出てくる)
#
# 回帰診断を詳しくみる
# てこ比
lev <- hatvalues(mbaf.lm); lev # てこ比
X <- model.matrix(mbaf.lm) # 説明変数行列
H <- X %*% solve(t(X) %*% X) %*% t(X) # ハット行列
diag(H) # てこ比の計算による導出
# 標準化残差
rstd <- rstandard(mbaf.lm); rstd # 標準化残差
se <- summary(mbaf.lm)$sigma # 残差標準偏差
mbaf.lm$residuals/(se*sqrt(1-lev)) # 標準化残差の計算による導出
# Cook 距離
x <- mbaf$入試得点
y <- mbaf$初年度成績
cookd <- cooks.distance(mbaf.lm); cookd # Cook 距離
b <- mbaf.lm$coefficients; b # 回帰係数
lm1 <- lm(y[-1] ~ x[-1])
b1 <- lm1$coefficients; b1 # 1番目のデータを除いた回帰係数
t(b-b1) %*% t(X) %*% X %*% (b-b1)/se^2/2 # 1番目のデータの Cook 距離
rstd^2*lev/(1-lev)/2 # Cook 距離の計算による導出
# 回帰推定値 - 残差プロット
x0 <- mbaf.lm$fitted.values # 回帰推定値
y0 <- mbaf.lm$residuals # 回帰残差
plot(x0, y0, type="n", xlab="回帰推定値", ylab="残差") #
text(x0, y0, rownames(mbaf), cex=0.8)
abline(h=0, lty=3)
title(main="回帰推定値 - 残差プロット")
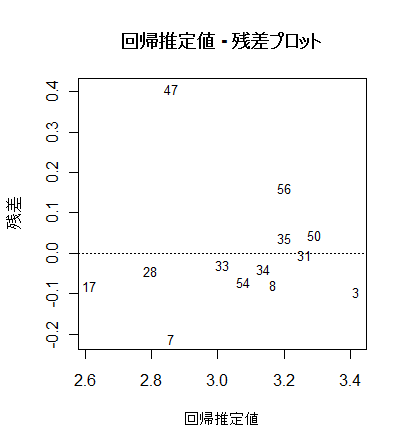
# 標準化残差 Q - Q プロット
a <- qqnorm(rstd, type="n", main="") # 標準化残差の Q - Q プロット(正規分布からのずれ)
text(a, rownames(mbaf), cex=0.8)
qqline(rstd, col="red")
title("標準化残差正規 Q-Q プロット")
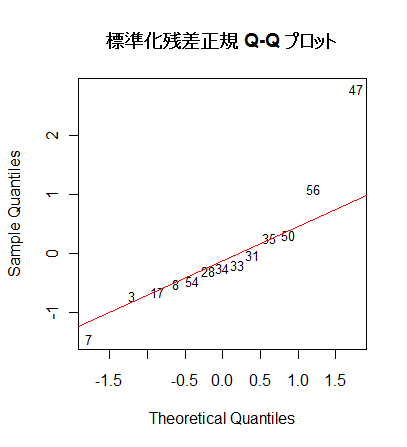
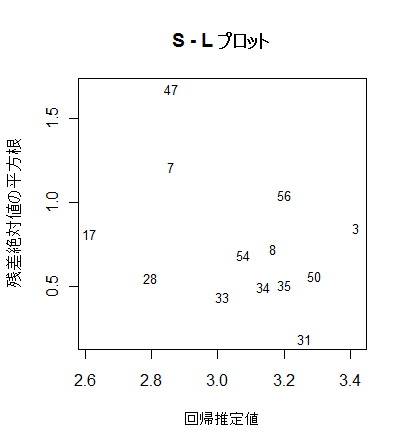
# S - L プロット
yr <- sqrt(abs(rstd)) # 標準化残差絶対値の平方根
plot(x0, yr, type="n", xlab="回帰推定値", ylab="残差絶対値の平方根") #
text(x0, yr, rownames(mbaf), cex=0.8)
title(main="S - L プロット")
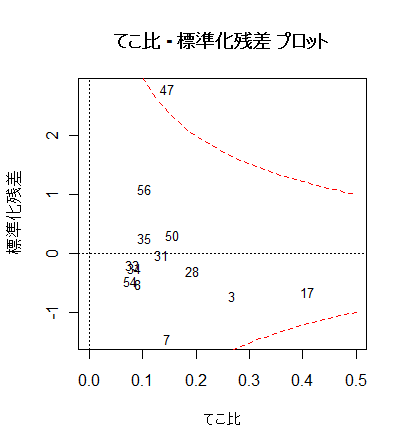
# てこ比 - 標準化残差 プロット
plot(lev, rstd, type="n", xlim=c(0,0.5), xlab="てこ比", ylab="標準化残差")
text(lev, rstd, rownames(mbaf), cex=0.8)
abline(h=0, lty=3)
abline(v=0, lty=3)
title(main="てこ比 - 標準化残差 プロット")
xx <- seq(0, 0.5, by=0.01)
yc <- .5*2*(1-xx)/xx # Cook 距離 0.5 となる標準化残差
yc1 <- sqrt(yc)
yc2 <- -yc1
points(xx, yc1, type="l", lty=2, col="red") # Cook 距離 0.5 線
points(xx, -yc1, type="l", lty=2, col="red")
|
| mba <- read.csv("mbagrade2.csv") | # データ読み込み |
| mbaf <- mba[mba[,1]=="F",] | # 女子データ |
| mbam <- mba[mba[,1]=="M",] | # 男子データ |
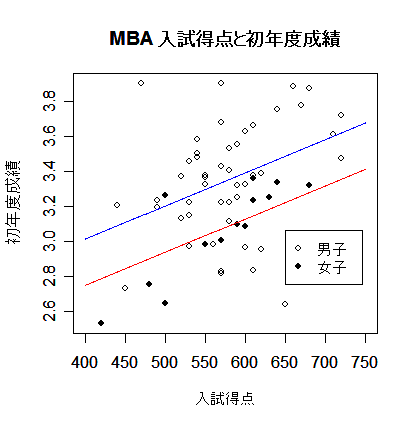
| mba.lm <- lm(初年度成績 ~ 性別 + 入試得点, data=mba) | # 重回帰分析 |
| summary(mba.lm) | # 結果表示 |
| plot(mba[,2:3], type="n", xlim=c(400,750)) | # |
| points(mbam[,2:3], pch=21) | # 男子データ(白丸) |
| points(mbaf[,2:3], pch=19) | # 女子データ(黒丸) |
| b <- mba.lm$coefficients | # 回帰係数 |
| x <- seq(400,750,by=1) | # |
| ym <- b[1] + b[2] + b[3]*x | # 男子回帰式 |
| yf <- b[1] + b[3]*x | # 女子回帰式 |
| lines(x, ym, type="l", col="blue") | # |
| lines(x, yf, type="l", col="red") | # |
| legend(locator(1), c("男子","女子"), pch=c(21,19)) | # |
| title(main="MBA 入試得点と初年度成績") | # |
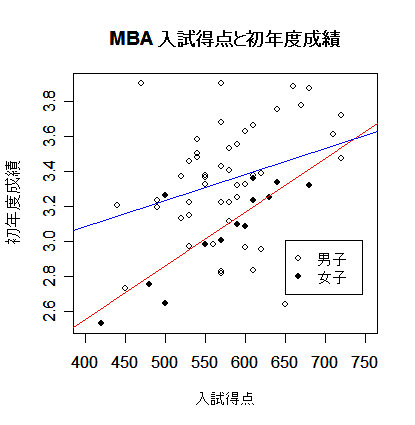
| mbaf.lm <- lm(初年度成績 ~ 入試得点, data=mbaf) | # 女子回帰 |
| summary(mbaf.lm) | # 結果表示 |
| mbam.lm <- lm(初年度成績 ~ 入試得点, data=mbam) | # 男子回帰 |
| summary(mbam.lm) | # 結果表示 |
| plot(mba[,2:3], type="n", xlim=c(400,750)) | # |
| points(mbam[,2:3], pch=21) | # 男子データ(白丸) |
| points(mbaf[,2:3], pch=19) | # 女子データ(黒丸) |
| abline(mbaf.lm, col="red") | # 女子回帰式 |
| abline(mbam.lm, col="blue") | # 男子回帰式 |
| legend(locator(1), c("男子","女子"), pch=c(21,19)) | # |
| title(main="MBA 入試得点と初年度成績") | # |
| mba2.lm <- lm(初年度成績 ~ 性別 + 性別 : 入試得点, data=mba) | # 性別ごとの回帰 |
| summary(mba2.lm) | # 結果表示 |
| anova(mba2.lm) | # 分散分析表示 |
k 個のパラメータ θ を持つ回帰モデル
| anova(mba.lm) | # 性別,入試得点重回帰の分散分析表 |
| AIC(mba.lm) | # 性別,入試得点重回帰モデルの AIC |
| n <- nrow(mba) | # 総データ数 |
| v2 <- anova(mba.lm)[3,2]/n | # 残差分散の最尤推定値(n で割る) |
| aic <- n*log(2*pi) + n*log(v2) + n + 2*4; aic | # 自由パラメータ数 4 の AIC |
| anova(mba2.lm) | # 男女別々回帰,残差分散共通の分散分析表 |
| AIC(mba.lm) | # 男女別々回帰,残差分散共通モデルの AIC |
| anova(mbaf.lm) | # 男子単回帰分散分析表 |
| anova(mbam.lm) | # 女子単回帰分散分析表 |
| AIC(mbaf.lm)+AIC(mbam.lm) | # 男女完全別々モデルの AIC |
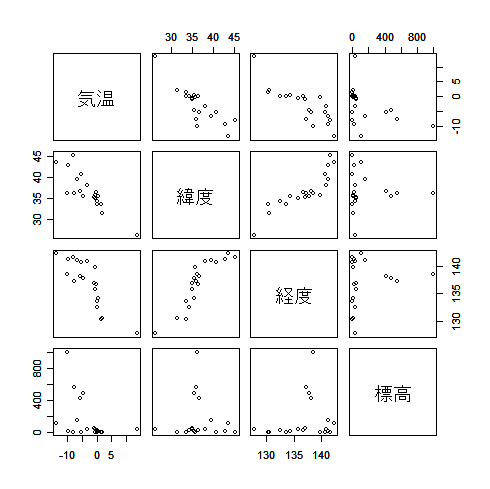
| kion <- read.csv("kion.csv") | # 気温データ読み込み |
| pairs(kion[,2:5]) | # 変数間散布図一覧 |
| cor(kion[,2:5]) | # 変数間相関 |
| kion1.lm <- lm(気温 ~ 緯度 + 経度 + 標高, data=kion) | # 3 変数重回帰 |
| summary(kion1.lm) | # 結果表示 |
| anova(kion1.lm) | # 分散分析表示 |
| n <- nrow(kion) | # データ数 |
| x0 <- rep(1,n) | # |
| x <- as.matrix(cbind(x0, kion[,3:5])) | # 説明変数行列 |
| se2 <- anova(kion1.lm)[4,3] | # 残差分散 |
| v <- se2 * solve(t(x) %*% x) | # 回帰係数の分散共分散行列 |
| sqrt(diag(v)) | # 回帰係数の標準誤差 |
| kion0.lm <- lm(気温 ~ 1, data=kion) | # 説明変数無し回帰 |
| anova(kion0.lm) | # |
| kion11.lm <- lm(気温 ~ 緯度, data=kion) | # 説明変数:緯度,回帰 |
| anova(kion11.lm) | # |
| kion12.lm <- lm(気温 ~ 経度, data=kion) | # 説明変数:経度,回帰 |
| anova(kion12.lm) | # |
| kion13.lm <- lm(気温 ~ 標高, data=kion) | # 説明変数:標高,回帰 |
| anova(kion13.lm) | # |
| kion21.lm <- lm(気温 ~ 緯度 + 経度, data=kion) | # 説明変数:緯度,経度,回帰 |
| anova(kion21.lm) | # |
| kion22.lm <- lm(気温 ~ 経度 + 標高, data=kion) | # 説明変数:経度,標高,回帰 |
| anova(kion22.lm) | # |
| kion23.lm <- lm(気温 ~ 緯度 + 標高, data=kion) | # 説明変数:緯度,標高,回帰 |
| anova(kion23.lm) | # |
| kion3.lm <- lm(気温 ~ 緯度 + 経度 + 標高, data=kion) | # 説明変数:緯度,経度,標高,回帰 |
| anova(kion3.lm) | # |
| AIC(kion0.lm) | # 説明変数無し回帰 AIC |
| AIC(kion11.lm) | # 説明変数:緯度,回帰 AIC |
| AIC(kion12.lm) | # 説明変数:経度,回帰 AIC |
| AIC(kion13.lm) | # 説明変数:標高,回帰 AIC |
| AIC(kion21.lm) | # 説明変数:緯度,経度,回帰 AIC |
| AIC(kion22.lm) | # 説明変数:経度,標高,回帰 AIC |
| AIC(kion23.lm) | # 説明変数:緯度,標高,回帰 AIC |
| AIC(kion3.lm) | # 説明変数:緯度,経度,標高,回帰 AIC |
| library(MASS) | # MASS ライブラリィー読み込み |
| null <- lm(気温 ~ 1, kion) | # 説明変数無し |
| full <- lm(気温 ~ 緯度 + 経度 + 標高, kion) | # 説明変数3つ |
| result <- stepAIC(null, scope=list(lower=null, upper=full), data=kion) | # 変数増減法 |
| summary(result) | # 結果表示 |
| cars | # R 付属データ 'cars' の呼び出し |
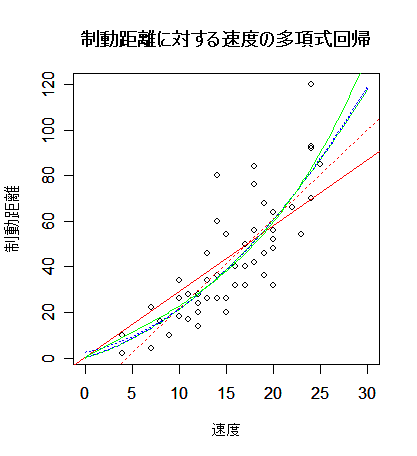
| plot(cars, xlim=c(0,30), xlab="速度", ylab="制動距離") | # cars の散布図 |
| title(main="制動距離に対する速度の多項式回帰") | # |
| y <- cars$dist | # 目的変数(制動距離) |
| x <- cars$speed | # 説明変数(速度) |
| car1.lm <- lm(y ~ x) | # 1次回帰 |
| abline(car1.lm, lty=3, col="red") | # 赤点線で表示 |
| summary(car1.lm) | # |
| car10.lm <- lm(y ~ 0 + x) | # 原点を通る1次回帰 |
| abline(car10.lm, col="red") | # 赤実線で表示 |
| summary(car10.lm) | # |
| x2 <- x^2 | # x の2乗を新しい変数で定義 |
| car2.lm <- lm(y ~ x + x2) | # 重回帰(2次式回帰) |
| b <- car2.lm$coefficients | # 回帰係数 |
| xv <- seq(0, 30, by=0.2) | # x の点列の定義 |
| yv <- b[1] + b[2]*xv + b[3]*xv^2 | # x の点列に対する2次回帰推定値 |
| lines(xv, yv, lty=3, col="blue") | # 青点線で表示 |
| summary(car2.lm) | # |
| car20.lm <- lm(y ~ 0 + x + x2) | # 原点を通る2次式回帰 |
| b <- car20.lm$coefficients | # 回帰係数 |
| yv <- b[1]*xv + b[2]*xv^2 | # x の点列に対する2次回帰推定値 |
| lines(xv, yv, col="blue") | # 青実線で表示 |
| summary(car20.lm) | # |
| x3 <- x^3 | # x の3乗を新しい変数で定義 |
| car3.lm <- lm(y ~ x + x2 + x3) | # 3変数重回帰(3次式回帰) |
| b <- car3.lm$coefficients | # 回帰係数 |
| yv <- b[1] + b[2]*xv + b[3]*xv^2 + b[4}*xv^3 | # x の点列に対する3次回帰推定値 |
| lines(xv, yv, lty=3, col="green") | # 緑点線で表示 |
| summary(car3.lm) | # |
| car30.lm <- lm(y ~ 0 + x + x2 + x3) | # |
| b <- car30.lm$coefficients | # 回帰係数 |
| yv <- b[1]*xv + b[2]*xv^2 + b[3]*xv^3 | # x の点列に対する3次回帰推定値 |
| lines(xv, yv, col="green") | # 緑実線で表示 |
| summary(car30.lm) | # |
| AIC(car1.lm) | # 1次回帰の AIC |
| AIC(car10.lm) | # 原点を通る1次回帰の AIC |
| AIC(car2.lm) | # 2次式回帰の AIC |
| AIC(car20.lm) | # 原点を通る2次式回帰の AIC |
| AIC(car3.lm) | # 3次式回帰の AIC |
| AIC(car30.lm) | # 原点を通る3次式回帰の AIC |