東京国際大学

統計学の応用(b)

東京大学大学院農学生命科学研究科　大森宏

講義プリントサイト：http://lbm.ab.a.u-tokyo.ac.jp/~omori/kokusai/kokusai06_index.htm

携帯解答サイト： http://lbm.ab.a.u-tokyo.ac.jp/~omori/k/

QRコード

１. この講義のねらい

　前期の統計学の応用(a)では，正規分布理論に基づいて，１変量データに対する統計解析を説明した． 統計学の応用(b)では，多変量データやカテゴリーデータなどの質的データを取り扱う．まずは， 前期の復習を行い．その後２変量データの重要な解析法である回帰分析を行う．

２. 統計学の応用(a)の復習

2-1. データ（標本）の代表値

数量データ：x1， x2，…，xn
→サンプルサイズ（標本の大きさ）：n

データの中心の位置を表す
→（標本）平均：x- ＝ （1/n）Σi xi ＝ (x 1 ＋ x2 ＋ … ＋ xn ) / n

データのちらばりの程度を表す
→標本分散：s 2 ＝ （1/n−1）Σi （x i − x-）2
　　　 ＝ ｛（x1 − x-）2 ＋（x2 − x-）2 ＋ … ＋ （xn − x-）2 ｝ /（n−1）
→標本標準偏差（SD：Standard Deviation）：s（標本分散の平方根）

2-1. 例題 1

以下のデータの代表値を小数第２位まで（小数第３位まで求めて四捨五入する）求めよ． 計算には電卓等を用いてよい．解答は携帯サイトで送信(半角数字) するか紙に記入すること．

9，4，6，5，-4，2，-1, 3

問題１：標本平均
問題２：標本分散
問題３：標本標準偏差

2-2. 平均の信頼区間

平均 μ，分散 σ2，の正規分布 から大きさ n の標本 x i 〜 N( μ，σ2 ) を抽出．
→標本平均の分散：Var[x-] ＝ σ2/n
→標本平均の標準偏差（標準誤差 SE：Standard Error）：sd[x-] ＝ σ/√n
→標本平均の分布： x- 〜 N( μ，σ2/n )
→標準化 z ＝ √n (x- − μ )/σ 〜 N（0，1）：標準正規分布
→分散 σ2 未知 →標本分散 s 2 で推定
→ t 値： t ＝ √n (x- − μ )/s 〜 t（n−1）：自由度 n−1 の t 分布
→自由度 n − 1 の t 分布の 97.5％分位点 t0
→Pr[ − t0 ＜ √n (x- − μ )/ s ＜ t0 ] ＝ 0.95
→Pr[ x- − t0 s / √n ＜ μ ＜ x- ＋ t0 s / √n　] ＝ 0.95
→母集団平均 μ の 95％ 信頼区間

2-2. 例題 1 (続き)

例題のデータから母平均の 95％ 信頼区間（x- ± d ）を求める． 以下の問題に答えよ．
問題４：用いる t 分布の 97.5％分位点 t0 を表から選べ
問題５：標本平均の標本標準偏差
問題６：信頼区間の幅 d

2-3. 平均に対する仮説検定

例題のデータは，リハビリ方式 A を３ヶ月行ったときの，身体能力の増加ポイントであるとする． リハビリを行わなかったときの身体能力の増加は平均的にみて無いことが知られている．
リハビリ方式 A が意味のあるものであるかどうか統計的に検定する．
リハビリの効果が無いと仮定すると，身体能力の増加ポイントの平均は０であると期待される．よって，

帰無仮説，H0：μ＝ 0（リハビリの効果認められない）
対立仮説，H1：μ≠ 0（リハビリの効果認められた）

と定式化される．仮説検定を行ったときには以下の２種類の誤りがある．過誤の確率は小さいほどよい．

統計的検定における2種類の過誤
  仮説の棄却 仮説の採択
仮説が真のとき 第１種の過誤 正解
仮説が偽のとき 正解 第２種の過誤

有意水準：帰無仮説（H0）が真のとき，仮説が棄却される確率．つまり第１種の過誤 の確率である．

仮説検定の手順．帰無仮説のもとでは，
→標本平均の分布：x- 〜 N( 0，σ2/n )
→標準化 z ＝ √n x- /σ 〜 N（0，1）（標準正規分布）
→分散 σ2 未知 →標本分散 s 2 で推定
→ t 値： t ＝ √n x- /s 〜 t（n−1）（自由度 n−1 の t 分布）
→自由度 n − 1 の t 分布の 97.5％分位点 t0
→絶対値 |t| 値：√n |x-| /s ＞ t0
　　→帰無仮説を棄却し，リハビリに効果が認められたと判断
→絶対値 |t| 値：√n |x-| /s ＜ t0
　　→帰無仮説を採択し，リハビリに効果が認められないと判断

2-3. 例題 1 (続き)

仮説検定における以下の問に答えよ．
問題７：t 分布の 97.5％分位点 t0 を用いたときの両側 仮説検定の有意水準（％単位）
問題８：絶対値 |t| 値
問題９：帰無仮説採択（1），棄却（2）のいずれか解答

2-4. 例題 2

以下のデータに関する問題を小数第２位まで（小数第３位まで求めて四捨五入する）求めよ． 計算には電卓等を用いてよい．解答は携帯サイトで送信(半角数字) するか紙に記入すること．

3.5，-1，7，1.5，11，5

問題１：標本平均（x-B ）
問題２：標本分散（sB2）
問題３：標本平均の分散
問題４：信頼区間の幅 d

2-4. ２つの平均の同等性に対する仮説検定

例題１のデータは，リハビリ方式 A を３ヶ月行ったときの，身体能力の増加ポイントであるとする． 例題２のデータは，リハビリ方式 B を３ヶ月行ったときの，身体能力の増加ポイントであるとする． リハビリを行わなかったときの身体能力の増加は平均的にみて無いことが知られている．
リハビリ方式 A と B の平均的な効果に違いがあるかどうかを統計的に検定する．
リハビリ方式 A の平均的な効果を μA，リハビリ方式 B の平均的な効果を μB とする．

帰無仮説，H0：μA ＝ μB （リハビリ方式 A と B の効果に違いは認められない）
対立仮説，H1：μA ≠ μB （リハビリ方式 A と B の効果は有意に異なる）

と定式化される．

仮説検定の手順．

　データ　標本数標本平均標本分散
標本 AnA x-A sA2
標本 BnB x-B sB2

1. A，B 共通の標本分散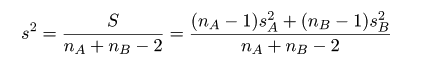： bunsan

2. 平均の差の標本分散：sd2 ＝ s 2 （1/nA ＋ 1/nB）
3. 平均の差の標本標準偏差（標準誤差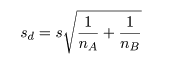）： difft
4. 検定統計量 t 値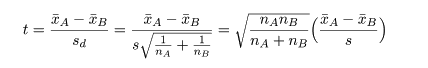： difft
5. 自由度 nA ＋ nB − 2 の t 分布の 97.5％分位点 t0
6. t の絶対値，
　　|t | ＞ t0 → 帰無仮説を有意水準 5 ％で棄却．
　　|t | ≦ t0 → 帰無仮説を棄却しない（受託する）．

2-4. 例題 2 (続き)

問題５：A，B 共通の標本分散
問題６：標本平均の差の絶対値
問題７：平均の差の標本分散
問題８：97.5％点 t0
問題９： t の絶対値

2-5. まとめ

リハビリ方式 A による身体能力の増加ポイントデータと リハビリ方式 B による身体能力の増加ポイントデータを要約すると，

　データ　標本数標本平均標本分散
標本 AnA ＝ 8 x-A ＝ 3 sA2 ＝ 16.57
標本 BnB ＝ 6 x-B ＝ 4.5 sB2 ＝ 17.8

となった．

例題 1 ：方式 A の平均に対する信頼区間と仮説検定

　方式 A の平均 μA の95％信頼区間と 帰無仮説（ H0 ： μA ＝ 0 ）の検定を行った．
　標本平均 x-A の分散は， s*A2 ＝ sA2/ nA ＝ 16.57/8 ＝ 2.07，となったので，標本平均の 標準誤差（標準偏差）は，s*A ＝ √2.07 ＝ 1.44 となった．
　一方，自由度 nA − 1 ＝ 7 の t 分布の 97.5％点が tA ＝ 2.36 であるので，方式 A の母集団 平均 μA に対する95％信頼区間の幅は，

dA ＝ tA ×s*A ＝ 2.36×1.44 ＝ 3.40

と なった．よって μA の95％信頼区間は，x-A ± dA ＝ 3 ± 3.40 ＝ -0.40 〜 6.40，となる．
　平均 μA の 95％信頼区間が 0 を含むので，

帰無仮説，H0： μA ＝ 0（リハビリの効果認められない）

は有意水準 5％の検定では棄却されない．
　実際，標本平均をその標準誤差で割った t 値は以下のように，

t ＝ x-A / s*A ＝ 3/1.44 ＝ 2.08 ＜ tA ＝ 2.36

自由度 nA − 1 ＝ 7 の t 分布の 97.5％点， tA ＝ 2.36 より小さいので，帰無仮説は 5％の 有意水準では棄却されず，方式 A は統計的に有意な効果が認められなかった，という 結論が得られる．

例題 2：方式 B の平均に対する信頼区間

　標本平均 x-B の分散は， s*B2 ＝ sB2/ nB ＝ 17.6/6 ＝ 2.97，となったので，標本平均の 標準誤差（標準偏差）は，s*B ＝ √2.97 ＝ 1.72 となった．
　一方，自由度 nB − 1 ＝ 5 の t 分布の 97.5％点が tB ＝ 2.57 であるので，方式 B の母集団 平均 μB に対する95％信頼区間の幅は，

dB ＝ tB ×s*B ＝ 2.57×1.72 ＝ 4.42

と なった．よって μB の95％信頼区間は，x-B ± dB ＝ 4.5 ± 4.42 ＝ 0.80 〜 9.82，となる．
　平均 μB の 95％信頼区間が 0 を含まないので，

帰無仮説，H0： μB ＝ 0（リハビリの効果認められない）

の検定を行えば，有意水準 5％では棄却される．方式 B は統計的に有意な効果が認められた， という結論が得られる．

例題 2 ：方式 A の平均と方式 B の平均との同等性に対する仮説検定

　方式 A の標本から推定された標本分散が sA2 ＝ 16.57 であり，方式 B の標本分散が sB2 ＝ 17.8 であったので，両者の分散には大きな違いがないと考えられた． このため，両者は同じ分散 σ2 を持つと考えた． 共通の分散の推定値は，

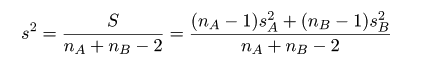bunsan
＝ ( 7×16.57 ＋ 5×17.8 )/12 ＝ ( 116 ＋ 89 )/12 ＝ 17.08

となった．一方，両集団の平均が等しいという帰無仮説（ H0：μA ＝ μB ）のもとでは，両集団の標本平均の差 x-A − x-B は，

x-A − x-B 〜 N( 0, σ2( 1/nA ＋ 1/nB）

という正規分布に従う．これより，標本平均の差の分散は，

sd2 ＝ s 2 （1/nA ＋ 1/nB） ＝ 17.08(1/8 + 1/6) ＝ 17.08×14/48 ＝ 4.98

と推定される．よって，標本平均の差の標準誤差は，sd ＝ √4.98 ＝ 2.23 となる．
　これより t の絶対値は，

|t | ＝ | x-A − x-B |/ sd ＝ 1.5/2.23 ＝ 0.62

となった．これは，自由度 nA ＋ nB − 2 ＝ 12 の t 分布の 97.5% 点 2.18 より小さい．よって， 両集団の平均が等しいという帰無仮説（ H0：μA ＝ μB ）は 5 ％の有意水準では棄却されない．

３. ２変量間の関係

３−１．相関

　標本（サンプル）に対し，２つの変数 x，y が測定されているとする． たとえば，x が身長(m)であり，y が体重(kg)である． 大きさ n の標本（サンプル）に対し，２つの変数の組のデータが，

（x1 ，y1 ）， （x2 ，y2 ）， …， （xn ，yn ）
であったとする． 変数間の関連性の強さを測る量として共分散（Covariance），Cov(x ，y ）がある． これは，変数に対する平均を，x- ＝ （1/n）Σi xi ， y- ＝ （1/n）Σi yi ，として，
Cov(x ，y ）＝ sxy ＝ （1/n−1）Σi （x i − x- ） （y i − y- ）
と定義される．

　共分散は測定単位により大きさが変わるので，これをおのおのの変数の分散， Var(x)，Var(y)，

Var(x) ＝ sx2 ＝ （1/n−1）Σi （x i − x- ) 2
で標準化したものが 相関係数 r，-1≦r≦1，であり，

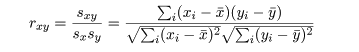
sokan

と定義される．これは，変数間の線形的関係の強さ，
（x が大きいと y も大きく，x が小さいと y も小さい，）
を測る指標で，｜r｜＝1 のときは， 変数 x，y は完全な直線関係にあり，r ＝0 のときは，線形的な関係 がない．r が 1 に近いときは，正の相関関係があるといい， r が -1 に近いときは，負の相関関係があるという．

データ散布図と相関係数
sokan sokan
sokan sokan

3-2．回帰分析

直線回帰

　２つの変数 x ，y に対し，y の値が x の値の動きにつれて 線形的に変化すると仮定される，つまり，

y ＝ a ＋ b x

という関係が成り立っていると考えられる場合である．これを y の x に 対する直線回帰といい，a ，b を回帰係数という． また，変数 y を従属変数，目的変数といい，変数 x を独立変数，説明変数と いう．

最小２乗法

　データに最もよくあてはまる直線回帰式を得るには，データ点 （xi ，yi ）， と回帰による推定点， （xi ，y^i ）， y^i ＝ a ＋ b xi ， の間の距離の２乗和 S が最小になるような回帰係数 a ，b を求める．つまり，

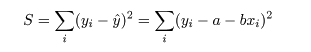
minsqure

を最小化する a ，b を求める問題に帰着する．これを最小２乗法という．

　これは，S を a ，b で偏微分して 0 とおくことによって得られる．つまり，

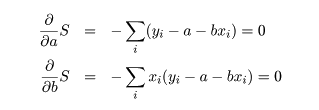
partial

の連立方程式を a ，b で解けばよい．これより，

coef

が得られる．b の最後の式は，

Σi （x i − x- ) y- ＝ y- Σi （x i − x- ) ＝ y- （Σi x i − nx- ) ＝ 0

より得られる．

例題 1

　下の表はアメリカのあるビジネススクール（MBA）での女子学生の入試得点と初年度成績である． 以下の問に答え，携帯で送信せよ．

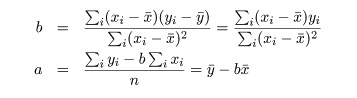
入試得点（x） 680 500 600 420 480 630 550 590 610 500 640 570 610
初年度成績（y） 332 265 309 253 276 326 299 310 324 327 334 301 336

問題１：初年度成績（y）の偏差平方和（小数点第２位）
問題２：入試得点（x）と初年度成績の偏差積和平方和（小数点第２位）
問題３：回帰係数（b）（小数点第２位）

kaiki

回帰式の統計モデル

　推定された直線回帰式がどの程度現実のデータに適合しているかを調べるために， 回帰式が従う統計モデルを考える．標本の格データ点， （xi ，yi ）， が，

yi ＝ a ＋ b xi ＋ ei ， ei 〜 N( 0，σ2 )

であると仮定する．ei は誤差（error），あるいは， 残差（residual）で，直線回帰 式では説明がつかない部分を表し，これが互いに独立に平均 0，分散 σ2 の正規分布に従うと仮定する．誤差の大きさが大きいときは，直線回帰式ではデータが説明できない と考える．

残差分散と回帰係数の標準誤差

　回帰で説明がつかない残差平方和 Se は，

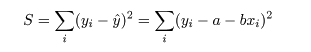
minsqure

で求められる．これの自由度は n−2 であるので（２つの回帰係数分の自由度を除く），回帰の 残差（誤差）分散は，

se2 ＝ Se/(n−2) ＝ Σi（yi −　 yi^ ）2 /(n−2)

で求められる．

　一般に，Var(yi ) ＝ σ2 であるとき，その定数 倍の分散は，

Var(ayi ) ＝ a2σ2， Var(Σiai yi ) ＝ Σiai 2 σ2

であり，従属変数 y のデータ yi は，

yi 〜 N( a ＋ b xi ，σ2 )

と分布するので，回帰係数 b の分散は，

Var(b ) ＝ σ2/Σi （x i − x- ) 2

となる．この分散の平方根を回帰係数 b の標準誤差という．

平方和分解と分散分析

　回帰式により， 従属変数 y のデータ yi は，

yi ＝ y^i ＋ (y^i − yi ) ＝ 回帰値 ＋ 残差

のように分解される．この分解に対応して従属変数データの総平方和 ST は，

ST ＝ Σi （y i − y- ) 2 ＝ Σi （y^i − y- ) 2 ＋ Σi （y i − y^i ) 2 ＝ SR ＋ Se
総平方和 ＝ 回帰平方和 ＋ 残差平方和

のように分解される．これを平方和の分解という．この分解に対応して自由度は，
n−1 ＝ 1 ＋ n−2
と分解される．

　データが直線回帰式でよく説明できるのは，回帰平方和が大きく，残差平方和 が小さい場合である．総平方和のうち回帰平方和で説明される割合を決定係数，もしくは 重相関係数の２乗といい，

決定係数（重相関係数の２乗）＝ R2 ＝（回帰平方和）/（総平方和）

で定義される．なお，重相関係数 R とは，データ y i と回帰値 y^i との間の相関係数である．これより， 以下の分散分析表ができる．

回帰分析の分散分析表
変動因平方和自由度平均平方F 値
回帰 SR 1 SR F ＝ SR/se2
残差 Se n−2 se2 ＝ Se/n−2 　
全体 ST n−1 　 　

回帰式の有意性の検定

分散分析による F 検定

従属変数 y が説明変数 x の回帰関係にないという 帰無仮説，

H0：b ＝ 0，

を考える．帰無仮説のもとでは，回帰平均平方 SR と残差分散 se2 がともに誤差 σ2 の不偏推定量になるので， その比 F 値が，

F ＝ SR/se2 〜 F（1，n−2），

という F 分布に従うことを利用して検定ができる．すなわち，分子，分母 自由度が 1，n−2 である F 分布 F（1，n−2）の95％点を F0 とすると，

F ＞ F0 → 帰無仮説を有意水準 5 ％で棄却（回帰関係が有意に認められる）
F ≦ F0 → 帰無仮説を棄却しない（回帰関係が認められない）

と定式化できる．
回帰係数の標準誤差による t 検定

回帰係数 b の推定値 b^ の分散は，

Var(b^ ) ＝ sb2 ＝ se2/Σi （x i − x- ) 2

と推定できるので，b^ の標準偏差（標準誤差）は， s b と推定 される．これより，回帰係数をその標準誤差で割った t 値が，帰無仮説のもとで，

t ＝ b^/s b 〜 t（n−2）

のように，自由度 n−2 の t 分布に従うことを利用して回帰係数の検定が行える．すなわち， 自由度 n−2 の t 分布の 97.5％点を t0 とすると，

|t | ＞ t0 → 帰無仮 説を有意水準 5 ％で棄却（回帰関係が有意に認められる）
|t | ≦ t0 → 帰無仮説を棄却しない（回帰関係が認められない）

と定式化できる．この検定式を２乗した

t 2 ＞ t02

が分散分析の F 検定と同値であることに注意．

　回帰係数の標準誤差 s b を用いて， 回帰係数 b の信頼区間がつくれる．すなわち， 自由度 n−2 の t 分布の 97.5％点を t0 とすると， 回帰係数 b の 95％信頼区間の幅 d は，d ＝ t0 s b となるので， 95％信頼区間は，

b^ − t0 s b ＜ b ＜ b^ ＋ t0 s b

となる．

例題 1 の続き

問題４：残差平方和（小数点第２位）
問題５：残差分散（小数点第２位）
問題６：重相関係数の２乗（小数点第２位）
問題７：F 値（小数点第２位）
問題８：回帰係数（b）の標準誤差（小数点第３位）
問題９：回帰係数（b）の95％信頼区間の幅 d（小数点第２位）

F 分布

　U が自由度 m の χ2 分布に従い （U 〜 χ2（m））， また，V 〜 χ2（n）と 分布し，U と V が互いに独立であるとする．このとき， 2つの χ2 分布する確率変数をそのおのおのの自由度 で割った量の比を F 値といい，

F = (U/m)/(V/n)

は自由度 m，n の F 分布に従い，F 〜 F(m, n) と表記する． m を分子の自由度，n を分母の自由度という．

　ところで，回帰係数の推定値 b^ をその 標準誤差 sb で割った t 値は， 回帰関係がないという帰無仮説 H0，

H0：b＝0
のもとで自由度 n − 2 の t 分布に従う，すなわち，
t ＝ b^/sb 〜 t(n−2)
となる．この関係において，
t 2 〜 F(1, n−2)
が成り立つ．つまり，t 分布をより一般化したのが F 分布である．
この F 分布を用いた F 検定が，回帰分析や分散分析でよく用いられる．

例題 ２

　下の表はアメリカのあるビジネススクール（MBA）での 48 名の男子学生の入試得点（x）と 初年度成績（y）である．

入試得点（x） 590 550 520 560 540 440 680 520 610 490 620 580 600 590 570 640
初年度成績（y） 325 333 313 299 351 321 388 338 367 320 296 311 297 332 368 376
入試得点（x） 540 530 660 540 570 710 450 650 580 590 490 600 570 580 520 610
初年度成績（y） 348 346 389 359 343 361 273 264 354 356 324 363 323 323 338 338
入試得点（x） 620 530 670 550 530 570 570 600 550 720 570 530 720 580 610 470
初年度成績（y） 339 322 378 337 315 391 283 333 338 348 282 298 372 341 284 391

　回帰分析を行うために必要な統計量は以下のように計算された．

　入試得点（x）初年度成績（y） (x − x-)(y − y-)
平均576.67335.19　
偏差平方和190066.747921.3 28170.0

以下の問に答え，携帯で送信せよ．

問題１： x と y の相関係数（r）（小数点第３位）
問題２： x に対する y の回帰係数（b）（小数点第３位）

　問題２で求めた回帰係数を用いて回帰推定値（ y^ ）を算出し， 回帰残差（ y − y^ ）を求めた．すると，残差平方和は， Se ＝ 43746.2，となった．
　これより以下の分散分析表を完成させよ（×の欄には値が入らない）．

回帰分析の分散分析表
　変　動　因　　平　方　和　　自由度　 　平 均 平 方　　F 　　値　
　回　帰　　　　　
　残　差　　43746.2　　×
　全　体　　　××

問題３：残差の自由度
問題４：残差分散（小数点第１位）
問題５：F 値（小数点第２位）
問題６：重相関係数の２乗，R2（小数点第３位）
問題７：回帰係数（b）の標準誤差（小数点第３位）
問題８：回帰係数（b）のt値（小数点第２位）
問題９：回帰係数（b）の95％信頼区間の幅 d（小数点第３位）

mba

４. カテゴリー度数の解析

４−１．適合度検定

　K 個のカテゴリーに対する理論的度数（理想的状態での度数）， E1，…，EK，がわかっているとき，観測された度数， O1，…，OK，が理論的度数と一致しているとみなされるかどうかを検定する． これは，以下の量
chi0
が，理論的度数に従って観測度数が生成されるという帰無仮説のもとで，ある適当な自由度 （通常は K − 1）の χ2 分布に従うことを利用して検定する．また，各セルの観測度数がそれ程大きくない（10以下）ときは， イエーツの連続性の補正，
chi0
を施した方がよいとされている．

例

　サイコロが正しいものであるかどうか確かめるために，60回さいころをふったところ，出た目の数は，

サイコロの目 　1　　2　　3　　4　　5　　6　
回数 　8　　11　　12　　8　　11　　10　

となったしよう．サイコロが正しいかどうか，どのように調べたらよいだろうか．
　このような問題に答えるのが適合度検定である．これは，サイコロが正しいと考えたときに出ることが 期待される度数と実際の観測度数が有意に異なっているかどうかを検定するものである．サイコロが正しい 場合，出る目はすべて等しく 1/6 の確率で出現することが期待される．このため，各目の期待度数 は，60×1/6＝10 となる．これより，

サイコロの目 　1　　2　　3　　4　　5　　6　
観測度数 　8　　11　　12　　8　　11　　10　
期待度数 　10　　10　　10　　10　　10　　10　

という表がかける．観測度数が期待度数からどの程度離れているかは，χ2 値，
χ2 ＝ (8−10)2／10 ＋ (11−10)2／10 ＋ (12−10)2／10 ＋ (8−10)2／10 ＋ (11−10)2／10 ＋ (10−10)2／10
＝ 4／10 ＋ 1／10 ＋ 4／10 ＋ 4／10 ＋ 1／10 ＋ 0／10 ＝ 14／10 ＝ 1.4
を計算する．この χ2 値が，サイコロが正しいという帰無仮説のもとで，自由度 6−1＝5 の χ2 分布に従うことを利用して検定ができる．

χ2 分布の％点
自由度90％95％99％
12.713.846.64
24.615.999.21
36.257.8111.34
47.789.4913.28
59.2411.0715.09

　χ2 ＝1.4 を上の χ2 分布の表の自由度5の値と比べると， 有意でない，つまり，サイコロが正しいという帰無仮説は棄却されないことがわかる． これより，サイコロは正しいと考えることができる．

４−２．２元分割表

独立性の検定

　n 標本を２つの変数 A，B で分類したとき，２つの変数に関連があるかを調べたい． 変数 A を集団属性（集団１，集団２），変数 B を反応パターン（反応１，反応２）とした とき，データは以下のようにまとめられる．

2 元分割表データ
　　反応１　　反応２　　計　　
　集団１　 n11 n12 n1・
　集団２　 n21 n22 n2・
　計　 n・1 n・2 n

　ここで，nij は，集団 i の標本の中で，反応 j を取った人数（度数） である．また，ni・ は集団 i の標本の大きさで， n・j は標本全体（大きさ n）の中で反応 j を取った人数 を表し，それぞれ周辺度数という．
　このような表において，集団で反応パターンに違いがなければ，集団 i で反応 j を取る確率は， 集団 i である確率 ni・/n に 集団 j である確率 n・j/n をかけた ni・n・j/ n2 となることが期待される．これより， 集団 i で反応 j を取る人数（度数）は， ni・n・j/n となることが期待される．これを独立性の仮定という．
　独立性の仮定の帰無仮説（H0）もとでは，集団 i で反応 j を取る期待度数は，

独立性の仮定下の 2 元分割表データ
　　反応１　　反応２　　集団周辺　
　集団１　 n1・ n・1/n n1・ n・2/n n1・
　集団２　 n2・ n・1/n n2・ n・2/n n2・
　反応周辺　 n・1 n・2 n

となる．このとき，独立性の帰無仮説 H0 のもとでは，以下の χ2 値が

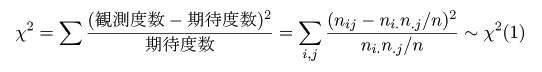
chai2

のように自由度 1 の χ2 分布に従うことを利用して，集団と反応が独立 であるかどうかの検定ができる．

比率（分布）の等質性の検定

　分割表は，世論調査やアンケート調査で，ある対象に対する好みや政策に対する賛否などを問うことがよくある． 性別や年齢層などの集団で意見が異なるかを調べたい場合にも用いられる．このときは， 集団で比率が異なるかどうかの検定を行う．このときは，集団の周辺度数 ni・ をあらかじめ設定した標本となり，しばしば， n1・ ＝ n2・ とする．検定の計算法は上記の独立性の検定と同じである．

例題１

　ある大学の学生250名をランダムに選び，ある商品に対する好みを尋ね性別で分類したところ 以下の表が得られた．この商品に対する好みと性別には関連があると考えてよいか．

性別と好みの２元分割表
　　好き　　嫌い　　計　　
　男　60 60 　120
　女　 40 90 　130
　計　 100 150 　250

　この問題を考えるには，帰無仮説として，商品の好みと性別は独立である（関連はない）と 仮定する．この仮説のもとでの期待度数を計算し，それと観測度数との違いの程度を計算すればよい． 計算は以下の表に値を埋めていくとやりやすい．

χ2 値の計算表
　　男・好き　　男・嫌い　 　女・好き　　女・嫌い　　計（χ2 値）　
観測度数（O）　60　60 　40　90　250
期待度数（E）　　　　　250
(O − E)2／E　　　　　

以下の問に答え携帯で送信せよ．

問題１：男性が好きと回答する期待度数（E）
問題２：男性が嫌いと回答する期待度数（E）
問題３：女性が嫌いと回答する期待度数（E）
問題４：男・好きのセルでの (O − E)2／E の値（小数第２位）
問題５：χ2 値（小数第１位）

例題１（続き）

　さきほどの例とは異なり，学生の人数が25人であった場合どうなるだろうか．男女比，好き嫌いの比 は同じであるとする．

性別と好みの２元分割表
　　好き　　嫌い　　計　　
　男　6 6 　12
　女　 4 9 　13
　計　 10 15 　25

　さきほどと同様に，帰無仮説として，商品の好みと性別は独立である（関連はない）と 仮定する．この仮説のもとでの期待度数を計算し，それと観測度数との違いの程度を計算すればよい．

χ2 値の計算表
　　男・好き　　男・嫌い　 　女・好き　　女・嫌い　　計（χ2 値）　
観測度数（O）　6　6 　4　9　25
期待度数（E）　　　　　25
(O − E)2／E　　　　　

問題６：χ2 値（小数第２位）

　質問に回答した学生の人数が250人から25人と1/10に減ると，χ2 値が減少する．これは， 独立性の帰無仮説を棄却するためには，多くの標本（サンプル）が必要なことを示している．

R×C 表

　変数 A，B のカテゴリーがそれぞれ R，C となったときも同様の検定が行える．このときの χ2 値は独立性の帰無仮説のもとで自由度 (R−1)(C−1) の χ2 分布に従うことを利用して検定ができる．

例題１（続き）

　カップヌードルの好みは年代によって違いがあるかどうかを調べた．10代，20代，30代，40代 の被験者をそれぞれ100名ずつ選び，好みを聞いたところ以下の表がえられた．

年代による好みの違い
　　10代　　20代　　30代　 　40代　    計  
　カップヌードル　41 50 　57　56　204
　シーフードヌードル　 59 50 　43 　44　196
　計　 100 100 100 100 400

グラフに図示すると以下のようになった．
konomi

問題７：好みの違いの表の自由度
問題８：好みの違いのχ2 値（小数第２位）

　グラフにすると，若い人（10代）はシーフードヌードルを好み，比較的年配の人（30代，40代）は カップヌードルを好む傾向にありそうだが，

帰無仮説：ヌードルの好みは年代により異ならない

は，有意水準5％で棄却できなかった．30代と40代では，好みに違いがなさそうなので，検定の自由度を減らす ため，30代と40代でまとめて，10代，20代，30・40代の３つのカテゴリーにまとめてみた．

問題９：好みの違いのχ2 値（小数第２位）

すると，帰無仮説は有意水準５％で棄却され，ヌードルの好みは年代により異なることが統計的に示された．

参考文献

  1. 『心理・教育のための統計法（第 2 版）』，山内光哉，1998，サイエンス社
  2. 『実践生物統計学−分子から生態まで−（第 1 章，第 2 章）』， 東京大学生物測定学研究室編（大森宏ら）， 2004，朝倉書店
  3. 『フリーソフトウェア R による統計的品質管理入門』，荒木孝治　編著，2005，日科技連
  4. 『The R Tips（データ解析環境Rの基本技・グラフィックス活用集）』，船尾暢男，九天社
  5. 『工学のためのデータサイエンス入門（フリーな統計環境Rを用いた統計解析）』間瀬茂ら，2004, 数理工学社
  6. 『生のデータを料理する』，岸野洋久，日本評論社
  7. 『統計的官能検査法』，佐藤信，1985, 日科技連
  8. 『データマインニング事例集』，上田太一郎，1998，共立出版
Copyright (C) 2006, Hiroshi Omori. 最終更新：2006年12月20日