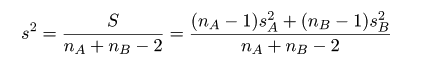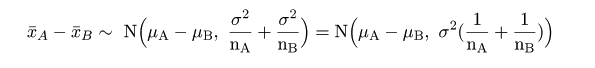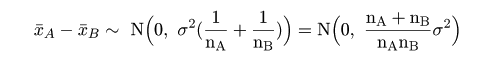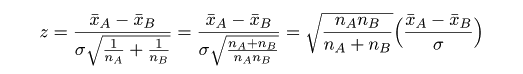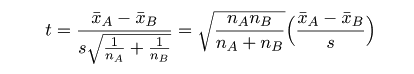- 一様分布からの標本の平均値の分布
-
(0,1)一様分布が有名で,一様乱数(一様分布する
確率変数の実現値)を生成する機能がパソコンに組み込まれている.
一様分布からの標本の大きさを増やしていくと,標本平均の分布は正規分布
に近づく(中心極限定理)
(0,1)一様分布からの大きさ n 標本の標本平均の1万回試行シミュレーション分布.
n = 12 では正規分布を上書き
3-6. データへの正規分布の当てはめ
データの標本平均と標本分散(標準偏差)を正規分布の平均と分散(標準偏差)とみなす.
データの当てはまり具合は,累積分布で比較する
→ コルモゴルフ・スミルノフ(Kolmogorov - Smirnov)検定
正規 Q-Q プロットを用いるとさらによくわかる.
3-7. 正規分布に基づく母数の区間推定
- 分散既知の場合の母平均 μ の区間推定
-
正規分布する母集団で分散がわかっている場合は,未知の平均に関する区間推定ができる.
いま,正規分布 N( μ,σ2 ) において,大きさ n の標本を
抽出したとき,標本平均 x- は,
x- ~ N( μ,σ2/n ) →
z = √n(x- - μ )/σ ~ N(0, 1)
と分布する.標準正規分布の 97.5%分位点は 1.96 であるので,
標準正規分布する確率変数 z が -1.96 から 1.96 に入る確率は 0.95 となる.つまり,
Pr[ - 1.96 < z < 1.96 ] = 0.95,
Pr[ - 1.96 < √n(x-
- μ )/σ < 1.96 ] = 0.95,
Pr[ - 1.96×σ/ √n < x- - μ < 1.96×σ/ √n ] = 0.95,
Pr[ - 1.96×σ/ √n < μ - x-< 1.96×σ/ √n ] = 0.95,
Pr[ x- - 1.96×σ/ √n < μ
< x- + 1.96×σ/ √n ] = 0.95,
となる.最後の式を母集団平均 μ の 95% 信頼区間と言う.
このように,母数の信頼区間を標本から推定することを区間推定という.
- 例題4
-
過去の経験から分散が 9 であることがわかっている正規母集団から大きさ 16 の標本を抽出
したところ,標本平均が 1.5 であった.標準正規分布の 97.5% 分位点を 1.96
として,母平均 μ の 95% 信頼区間を求めよ.
- 解答:
-
σ=√9=3,√n=√16=4,より,1.96×σ/ √n=1.96×3/4=1.47
よって,1.5 ± 1.47,つまり, 0.03 < μ < 2.97 が母平均 μ の 95% 信頼区間
となる.
- 95% の意味
-
同じ正規母集団から標本抽出を繰り返すと,毎回標本平均として異なる値がえられ,それに
対応して信頼区間も異なる.この信頼区間の 95% が真の平均 μ を含む,という意味である.
つまり,100回の標本抽出により,100 個の信頼区間を作ったら平均的にみて,95 個の信頼区間が
真の平均 μ を含むことが期待できる.
下の図は,平均 0 分散 2 の正規分布 N( 0, 2 ) から大きさ 10 の標本を取りだし,分散が既知であるとして,
母平均に対する信頼区間を 100 個生成したものである."×" が標本平均を示す.左の "*" は,信頼区間
が母平均の真値 0 を含まなかった場合である.
3-8. 正規分布から派生する分布
- 3-8-1. χ2分布
-
標準正規分布する確率変数の 2 乗は自由度(df: degree of freedom)
1 の χ2 分布
(χ2(1) )に従う.
互いに独立に標準正規分布する確率変数の 2 乗の n 個の和は,
自由度 n の χ2 分布
(χ2(n))に従う.
[(標準正規分布データ)2の n 個の和] ~
χ2(n)
zi ~ N(0, 1) →
zi2 ~
χ2(1) →
z12+ … +
zn2 ~
χ2(n)
xi ~
N( μi,
σi2 ) →
(xi -
μi)/σi
~ N(0, 1)
→
(x1 -
μ1)2 /
σ12
+ … + (xn -
μn)2 /
σn2 ~
χ2(n)
自由度 n の χ2 分布の平均と分散はそれぞれ n,2n である.
- 標本分散の分布
-
xi を正規分布
N( μ,σ2 ) からの大きさ n の標本とする.
標本平均を
x- =
(x1 + … +
xn )/n =
(∑i
xi )/n,
標本分散を
s2 =
{ (x1 - x-
)2 + … +
(xn - x-
)2 }/(n - 1) =
{∑i
(xi - x-
)2 }/(n - 1)
,
とすると,
∑i
(xi - μ
)2 =
∑i
(xi -
x- + x- -
μ )2 =
∑i
(xi -
x- )2 +
n(x- - μ )2
と変形できる.一方,
xi ~
N( μ,σ2 ) →
(xi -
μ )/σ ~ N(0, 1) →
∑i
(xi - μ )2 /
σ2 ~
χ2(n)
x- ~ N( μ,σ2/n ) →
√n(x- - μ )/σ ~ N(0, 1) →
n(x- - μ )2/
σ2 ~ χ2(1)
であるので,
(n - 1)s2 /σ2
= ∑i
(xi -
x- )2/
σ2 =
∑i
(xi - μ )2/
σ2 -
n(x- - μ )2/
σ2
~ χ2(n) - χ2(1)
= χ2(n-1)
つまり,標本分散を自由度(n - 1)倍したものを,母集団分散(母分散)
で割ったもの,
(n - 1)s2
/σ2,
は,自由度 n - 1 の χ2 分布に従うことがわかる.
- 標本分散の不偏性
-
自由度 n - 1 の χ2 分布の平均は n - 1 なので,
(n - 1)s2
/σ2の平均は n - 1,つまり,
E[ (n - 1)s2
/σ2 ] =
(n - 1) E[ s2 ]
/σ2 =
n - 1
E[ s2 ]
/σ2 = 1 →
E[ s2 ] = σ2
が成り立つ.これは,標本分散 s2 の期待値(平均)が
母分散 σ2 になることを示す.
正規母集団(正規分布する母集団)から標本抽出を繰り返して,標本分散を求めると,その平均が
真の値 σ2 になることを示す.これを不偏性という.
標本分散 s2 は,
母分散 σ2 の不偏推定値であることがわかる.
つまり,母分散の推定値として,偏差平方和 ∑i
(xi -
x- )2 を標本の大きさ n ではなく,
n - 1 で割って,s2 =
{∑i
(xi - x-
)2 }/(n - 1)
とするのは,母分散の不偏推定値をえるためである.このため,標本分散をとくに不偏分散と
呼ぶこともある.
- 母分散 σ2 の区間推定
-
正規母集団 N( μ,σ2 ) から大きさ n の
標本を取り出したとき,標本分散 s2 は,
(n - 1)s2 /σ2
~ χ2(n-1)
と分布する.自由度 n - 1 の χ2 分布の 2.5%分位点を
χ1,97.5%分位点を
χ2,とすると,
Pr[ χ1 <
(n - 1)s2 /σ2
< χ2 ] = 0.95,
Pr[ 1/χ1 >
σ2 /
(n - 1)s2
> 1/χ2 ] = 0.95,
Pr[ (n - 1)s2
/χ1 >
σ2
> (n - 1)s2
/χ2 ] = 0.95,
となる.最後の式を母集団分散
σ2 の 95% 信頼区間と言う.
- 例題5
-
正規母集団から大きさ 10 の標本を取りだしたところ,標本分散(不偏分散)は 3 であった.
母分散 σ2 の 95% 信頼区間を求めよ.
ただし,自由度 9 の χ2 分布の 2.5%分位点は
2.7,97.5%分位点は19.0である.
- 解答
-
(n - 1)s2
/χ1 = 9×3/2.7 = 10,
(n - 1)s2
/χ2 = 9×3/19 = 1.42,であるので,求める区間は,
1.42 < σ2 <10,である.
- 3-8-2. t 分布
-
標準正規分布に従う確率変数を z,(z ~ N(0,1)),
自由度 n の χ2 分布に従う
確率変数を V,(V ~ χ2(n)),
とし,両者が独立であるとすると,その比 t は,自由度 n の t 分布,t(n),に従う.
t = z /√(V /n) ~ t(n)
- 分散未知のときの標本平均の分布
-
正規母集団 N( μ,σ2 ) から大きさ n の
標本を取り出したとき,標本平均 x- を標準化したもの z は,
z = √n( x- - μ )/σ ~ N(0, 1)
と標準正規分布に従うが,母標準偏差 σ が未知であるときこれを標本標準偏差 s で置き換えた
ものを t 値といい,自由度 n - 1 の t 分布に従う.
これは,標本分散の分布から
V = (n - 1)s2
/σ2 ~ χ2(n-1)
であり,比をとると,V /(n-1) = s2
/σ2 であるので,
t = z /√{V /(n-1)} = { √n( x- - μ )/σ }/
{ s /σ }
= √n( x- - μ )/s ~ t(n-1)
となる.
- 分散未知のときの母平均 μ の区間推定
-
正規母集団 N( μ,σ2 ) から大きさ n の
標本を取り出したとき,標本平均が x- で標本分散が
s2 であるとすると,t 値は
t = √n( x- - μ )/s ~ t(n-1)
であるので,自由度 n - 1 の t 分布の 97.5%分位点 t0 と
すると,
Pr[ - t0 < √n(x-
- μ )/ s < t0 ] = 0.95,
Pr[ - t0 s
/ √n < x- - μ <
t0 s / √n ] = 0.95,
Pr[ - t0 s
/ √n < μ - x- <
t0 s / √n ] = 0.95,
Pr[ x- - t0 s
/ √n < μ < x- +
t0 s / √n ] = 0.95,
となる.最後の式を母集団平均 μ の 95% 信頼区間と言う.
- 例題6
-
正規母集団から大きさ 16 の標本を抽出したところ,標本平均が 1.5 で,標本分散が
9 であった.母集団平均 μ の 95% 信頼区間を求めよ.
ただし,自由度 15 の t 分布の 97.5%分位点を2.13とする.
- 解答
-
t0 s / √n = 2.13×√9/√16 = 1.60,
よって,1.5 ± 1.60,つまり, -0.1 < μ < 3.10 が母平均 μ の 95% 信頼区間
となる.
母集団分散が σ2 = 9
とわかっていた例題4の母平均 μ の 95% 信頼区間,0.03 < μ < 2.97,より幅が広くなることに
注意.
- F 分布
-
U が自由度 m の χ2 分布に従い
(U ~ χ2(m) ),
また,V ~ χ2(n) と
分布し,U と V が互いに独立であるとする.このとき,
2つの χ2 分布する確率変数をそのおのおのの自由度
で割った量の比を F 値といい,
F = (U/m)/(V/n)
は自由度 m,n の F 分布に従い,F ~ F(m, n) と表記する.
自由度 n - 1 の t 分布に従うt 値,
t = z /√{V /(n-1)}
= √n( x- - μ )/s ~ t(n-1),
において,
t 2 ~ F(1, n-1)
である.つまり,t 分布をより一般化したのが F 分布である.
回帰分析や分散分析で用いられる.
4. 仮説検定
4-1. 帰無(きむ)仮説(H0)と対立仮説(H1)
統計学で扱う仮説とは,母集団に対する断定や推測.たとえば,
- 母集団は正規分布に従っている.
- 母集団平均は 0 である.
- 母集団 A と母集団 B の平均は等しい.
などである.
統計的仮説検定で用いられる仮説は,まず,帰無仮説という形式で与えられる.
帰無仮説は棄却されることに意味がある仮説である.
帰無仮説と反対の仮説を対立仮説という.
上の3番目の例でみると,
帰無仮説:
母集団 A と母集団 B の平均は等しい.
(H0: μA = μB)
対立仮説:
母集団 A と母集団 B の平均は等しくない.
(H0: μA ≠ μB)
母集団 A と母集団 B は異なる処理(薬の投与など)をしているので,実験の目的
は,母集団 A と母集団 B の平均は異なる(処理効果がある)ことを言いたい
(対立仮説が正しいことを望む)のだが,まずは
「等しい(処理効果無し)」と仮定してみようという考え方.
数学の背理法と似た論理.
背理法:√2 が無理数であることを証明するため,まず√2 が有理数であると仮定し,矛盾があることを
示す.つまり,有理数であることは絶対ありえない(確率 0 である!)ことを示す.
この矛盾は,そもそも√2 を有理数とした仮定が誤っていたからであると考え,有理数という仮定を
棄却して,無理数であることを証明する.
4-2. 有意水準
検定とは,帰無仮説を受託(採択)するか
棄却(対立仮説の採択)するかを,母集団からの標本から判定すること.
検定のため,標本から算出される t 値などを検定統計量という
統計的仮説検定では,たとえば2つの母集団平均が等しいという帰無仮説を考えると,
この帰無仮説のもとで,検定統計量(標本平均の差に基づく t 値など)以上
(もしくは未満)の値が得られる確率を求める.
くだけた言い方をすれば,帰無仮説が正しいとしたときに,標本のようなデータが得られる確率
を求める.
これが十分小さい(ほとんどありえない)ときは,平均が等しいと仮定したことが誤りであったと判断して
帰無仮説を棄却し,2つの母集団平均には差があると結論づける.
この確率がそれほど小さく
ない場合は,このような統計量が得られることもありえると考え,帰無仮説を採択し,平均が等しいと考え
てもよいとする.
棄却か採択かの判断の基準となる確率を有意水準といい,
5 % や 1 % がよく用いられる.
- 例題4-1
- 通常の飼育方式では,鶏の1ヶ月の成長量が平均 100g,標準偏差 10g であることが知られて
いるとする.新方式 A による飼育方法を 25 羽で試したところ,平均成長量が 105g となった.新方式
でも標準偏差は変わらないものとして,新方式 A は通常の飼育方式と成長量が有意に異なるか
検定せよ.ただし,以下の標準正規分布の分位点(パーセント点)を用いよ.
標準正規分布の分位(パーセント)点
| 確率 |
0.95 | 0.975 | 0.99 | 0.995 |
| 分位点 |
1.64 | 1.96 | 2.33 | 2.58 |
- 解答例
- 新方式による成長量の母集団平均を μ とおき,通常の飼育方式の成長量の
母集団平均を μ0 = 100 とおく.題意より,新方式での成長量の標準
偏差は,通常の飼育方式と等しい σ0 = 10 とみなせる.
この問題での帰無仮説(H0)と対立仮説(H1)は,
H0:μ = μ0
H1:μ ≠ μ0
と定式化される.検定に用いる検定統計量は,標本平均を標準化した z 値の絶対値
である.
標本の大きさ n = 25 の標本の標本
平均 x- = 105より,
|z | =
√n | x- - μ0 |/σ0
=5(105-100)/10=2.5
である.新方式の標本平均の標準化値の絶対値 |z | = 2.5 は,両側 5 %点(片側 2.5 %点)
の 1.96 よりは
大きく,両側 1 %点(片側 0.5 %点)の 2.58 よりは小さい.
よって,新方式は通常方式と成長量は 5 %水準で有意に異なると言えるが,1 %水準
では有意でない.つまり,5 %有意である.
検定の結論の書き方
- 有意でない → 5 %で帰無仮説が棄却できないとき.
- 5 %有意 → 5 %で帰無仮説が棄却できたが 1 %では棄却できなかったとき.
- 1 %有意 → 1 %で帰無仮説が棄却できたとき.
4-3. 片側検定と両側検定
実験状況によっては,薬投与などの処理を行った集団(処理群)平均
μA が,薬を投与しない
集団(対照群)の平均 μB より小さくなることはないことが事前に
わかっているような場合が
ある.このようなとき,
帰無仮説,H0: μA =
μB
対立仮説,H0: μA >
μB
となる.これは,事前情報より,μA < μB となる可能性
をまったく考えない場合である.
このため検定には,片側 5 %点や 1 %点を用いる.
- 例題4-2
- 通常の飼育方式では,鶏の1ヶ月の成長量が平均 100g,標準偏差 10g であることが知られて
いるとする.改良方式 B による飼育方法を25羽で試したところ,平均成長量が 103.5g となった.
改良方式は,通常方式より成長量が減少することがないことが知られている.
改良方式での標準偏差は変わらないものとして,改良方式 B は通常の飼育方式と
成長量が有意に増大したか
検定せよ.ただし,例題4-1の標準正規分布の分位点(パーセント点)を用いよ.
- 解答例
- 改良方式による成長量の母集団平均を μ' とおき,通常方式の成長量の
母集団平均を μ0 =100とおく.題意より,改良方式での成長量の標準
偏差は,通常の飼育方式と等しい σ0 = 10 とみなせ,また,
改良方式平均 μ' は通常方式平均 μ0 より
下回ることは想定されない.よって,対立仮説は片側となり,
この問題での帰無仮説(H0)と対立仮説(H1)は,
H0:μ' = μ0
H1:μ' > μ0
と定式化される.検定に用いる検定統計量は,標本平均を標準化した z 値
である.
標本の大きさ n = 25 の標本の標本
平均 x- = 103.5より,
z =
√n(x- - μ0 )/σ0
= 5(103.5-100)/10 = 1.75
である.片側検定なので,片側パーセント点を用いる.
改良方式の標本平均の標準化値 z = 1.75 は,片側 5 %点の 1.64 よりは
大きく,片側 1 %点の 2.33 よりは小さい.
よって,改良方式は通常方式と成長量は 5 %水準で有意に増大したと言えるが,1 %水準
では有意でない.
両側検定であれば,5 %水準でも有意にならなかったことに注意.つまり,改良方式と通常方式
の間には有意な差はみとめられなかった,という結論になった.片側検定の方が有意な結果
が出やすい.
4-4. 両側検定と信頼区間
母集団平均に対する両側検定は,母集団平均に対する信頼区間と大きな関係がある.
いま,帰無仮説(H0)と対立仮説(H1)が,
H0:μ = μ0
H1:μ ≠ μ0
であり,母分散 σ2 が既知のときを考える.
標本の大きさがnで,標本平均が x- であったとすると,母平均μに対する
95%信頼区間は,
Pr[ - 1.96 < √n(x-
- μ )/σ < 1.96 ] = 0.95,
Pr[ x- - 1.96×σ/ √n < μ
< x- + 1.96×σ/ √n ] = 0.95
となる.一方,
有意水準 5%で帰無仮説を受諾するのは,標準化値の絶対値
|z| = √n|x-
- μ0 |/σ が両側 5%点1.96以下のときである.つまり,
帰無仮説を受諾 ⇔ - 1.96 < √n(x-
- μ0 )/σ < 1.96
である.この両者の関係より,
帰無仮説を受諾 ⇔ 母平均の信頼区間に μ0 が含まれる.
帰無仮説を棄却 ⇔ 母平均の信頼区間に μ0 が含まれない.
が成り立つ
- 例題4-3
- 例題4-1を,母平均に対する信頼区間を構成することで検定せよ.
- 解答例
-
母平均 μ に対する 95%信頼区間は,
Pr[ x- - 1.96×σ/ √n < μ
< x- + 1.96×σ/ √n ] = 0.95
x- ± 1.96×σ/ √n →
105 ± 1.96×10/5 → 105 ± 3.92 → 101.08 ~ 108.92
となる.この信頼区間は,帰無仮説の平均 μ0 =100を含まない.
よって,帰無仮説は有意水準 5%で棄却される.
母平均 μ に対する 99%信頼区間は,標準正規分布の99.5%点2.58を用い,
Pr[ x- - 2.58×σ/ √n < μ
< x- + 2.58×σ/ √n ] = 0.99
x- ± 2.58×σ/ √n →
105 ± 2.58×10/5 → 105 ± 5.16 → 99.84 ~ 110.16
となる.この信頼区間は,帰無仮説の平均 μ0 =100を含む.
よって,帰無仮説は有意水準1%で棄却されず採択される..
4-5. 検定における2種類の過誤
検定は,仮説を棄却するか採択するかのいずれかであるが,
統計量は分布をもつので,この判定には間違いが起こることがある.
以下のように,この過誤には
2 種類がある.
統計的検定における2種類の過誤
| |
仮説の棄却 |
仮説の採択 |
| 仮説が真のとき |
第1種の過誤 |
正解 |
| 仮説が偽のとき |
正解 |
第2種の過誤 |
第1種の過誤が有意水準である.また,第2種の過誤の確率を β としたとき,
仮説が偽のとき正しく仮説を棄却する確率,1 - β,を検出力という.
よい検定は,第1種の過誤を固定したもとで検出力の高い検定方式である.
4-6. 母平均に対する t 検定
平均 μ,分散 σ2 がともに未知である正規母集団から
大きさ n の標本を抽出したところ,
標本平均が x-,標本分散が s2 であった.
帰無仮説 H0:μ = μ0,
対立仮説 H1:μ ≠ μ0,
の検定は,帰無仮説のもとで,分散既知のときに標本平均を標準化して
えられる z 値,
z =
√n ( x- - μ0 )/σ の標準偏差のところに
標本標準偏差 s を代入した t 値,
t =
√n ( x- - μ0 )/s,
が自由度 n-1 の t 分布に従うことを利用して検定できる.
- 例題4-4
- 通常の飼育方式では,鶏の1ヶ月の成長量が平均 100gであることが知られて
いるとする.新方式 A による飼育方法を 25 羽で試したところ,平均成長量が 105g であり,
標本標準偏差が 10g であった.新方式 A は通常の飼育方式と成長量が有意に異なるか
検定せよ.ただし,自由度 24 の t 分布の 97.5%パーセント点は 2.06 であり,
99.5%点は 2.80 である.
- 解答例
- 新方式による成長量の母集団平均を μ とおき,通常の飼育方式の成長量の
母集団平均を μ0 = 100 とおく.
この問題での帰無仮説(H0)と対立仮説(H1)は,
H0:μ = μ0
H1:μ ≠ μ0
と定式化される.検定に用いる検定統計量は,標本平均を標準化した t 値の絶対値
である.
標本の大きさ n = 25 の標本の標本
平均 x- = 105より,
|t | =
√n | x- - μ0 |/s
=5|105-100|/10=2.5
である.新方式の標本平均の標準化値の絶対値 |t | = 2.5 は,両側 5 %点(片側 2.5 %点)
の 2.06 よりは
大きく,両側 1 %点(片側 0.5 %点)の 2.80 よりは小さい.
よって,新方式は通常方式と成長量は 5 %水準で有意に異なると言えるが,1 %水準
では有意でない.つまり,5 %有意である.
4-5. 2 つの母集団平均に対する t 検定
2つの母集団 A,B があり,それぞれが平均を μA,μB,
分散を σA2,σB2 の正規分布に従って
いるが,その値は未知であるとする.いま,両集団の分散の値が等しく,
σA2=σB2=σ2,と仮定
できるとしよう.このとき,
帰無仮説,H0: μA =
μB
対立仮説,H1: μA ≠
μB
の検定は t 分布を用いて行える.
母集団 A から大きさ nA,母集団 B から大きさ nB の標本を抽出した.
母集団 A からの標本の標本平均が x-A,
標本分散が sA2 であり,母集団 B の
標本平均が x-B,
標本分散が sB2 であった.母集団 A,B が共通の
分散 σ2 をもつとすると,その推定値 s2 は
以下のように推定できる.
|
母集団 A からの標本の偏差平方和:
|
SA=(nA-1)sA2
|
|
母集団 B からの標本の偏差平方和:
|
SB=(nB-1)sB2
|
|
母集団 A,B 全体での偏差平方和:
|
S = SA + SB
=(nA-1)sA2+
(nB-1)sB2
|
|
母集団 A,B 共通の標本分散:
|
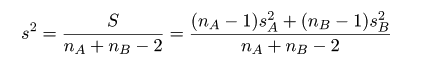
|
また,母集団Aの標本分布は,N(μA,σ2)であり,母集団Bでは,
N(μB,σ2)であることから,それぞれの標本平均は,
x-A ~ N(μA,σ2/nA),
x-B ~ N(μB,σ2/nB)
と分布する.これより,標本平均の差x-A-
x-Bは,
と分布する.
帰無仮説(H0: μA =
μB)のもとでは,μA-μB=0,なので,
標本平均の差は,
と分布する.これを標準化した z 値,
において,標準偏差 σ の代わりに標本標準偏差 s を代入した t 値,
が自由度 nA+nB-2 の t 分布に従うことを利用して検定ができる.
なお,母集団 A,B からの標本の大きさがともに等しく,
nA=nB=n であるときは,式がずっと簡単になる.
母集団A,Bで分散の同等性が疑われるときは,ウェルチの検定を用いる.
- 例題4-5
- 通常の飼育方式と新方式 A による飼育方法で,鶏の1ヶ月の成長量に差があるか
調べたい.通常の飼育方式で20羽を飼育したところ,平均成長量が100g,標本標準偏差
が9gであった.また,新方式 A による飼育方法を 25 羽で行ったところ,平均成長量が 105g であり,
標本標準偏差が 11g であった.新方式 A は通常の飼育方式と成長量が有意に異なるか
両集団の分散は等しいと仮定して検定せよ.
ただし,自由度 43 の t 分布の 97.5%パーセント点は 2.02 であり,
99.5%点は 2.70 である.
- 解答例
- 新方式による成長量の母集団平均を μ とおき,通常の飼育方式の成長量の
母集団平均を μ0 とおく.
この問題での帰無仮説(H0)と対立仮説(H1)は,
H0:μ = μ0
H1:μ ≠ μ0
と定式化される.両集団共通の標本分散と標本標準偏差は,
s2=(19×92+24×112)/(20+25-2)
=4443/43=103.33,
s=√103.33=10.17
となる.t値の絶対値は,
t=√{20×25/(20+25)}×|105-100|/10.17=√(100/9)×5/10.17
=1.64
である.
両集団の標本平均の差の標準化値の絶対値 |t|=1.64は,両側 5 %点(片側 2.5 %点)の
2.02より小さいので,新方式と通常方式の成長量は 5 %で有意に異ならない.つまり,
帰無仮説は棄却されない.
参考文献
- 『心理・教育のための統計法(第 2 版)』,山内光哉,1998,サイエンス社
- 『実践生物統計学-分子から生態まで-(第 1 章,第 2 章)』,
東京大学生物測定学研究室編(大森宏ら),
2004,朝倉書店
- 『フリーソフトウェア R による統計的品質管理入門』,荒木孝治 編著,2005,日科技連
- 『The R Tips(データ解析環境Rの基本技・グラフィックス活用集)』,船尾暢男,九天社
- 『工学のためのデータサイエンス入門(フリーな統計環境Rを用いた統計解析)』間瀬茂ら,2004, 数理工学社
- 『生のデータを料理する』,岸野洋久,日本評論社
- 『統計的官能検査法』,佐藤信,1985, 日科技連
Copyright (C) 2006, Hiroshi Omori. 最終更新:2006年 7月10日