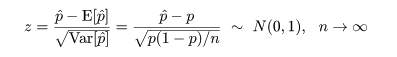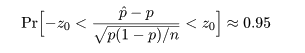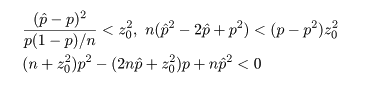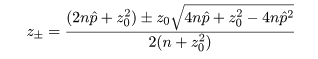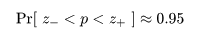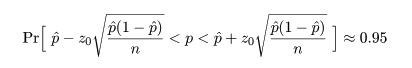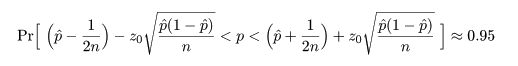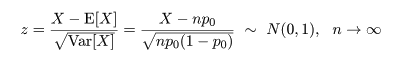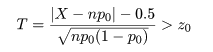2008.10.2

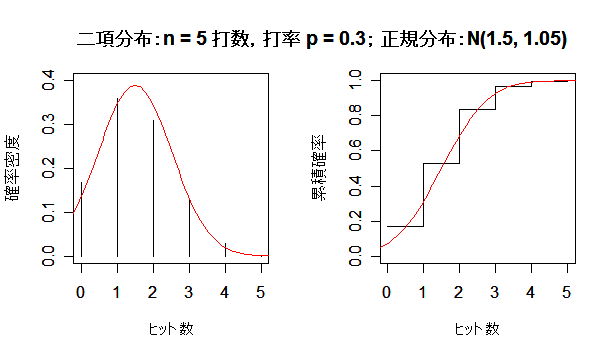
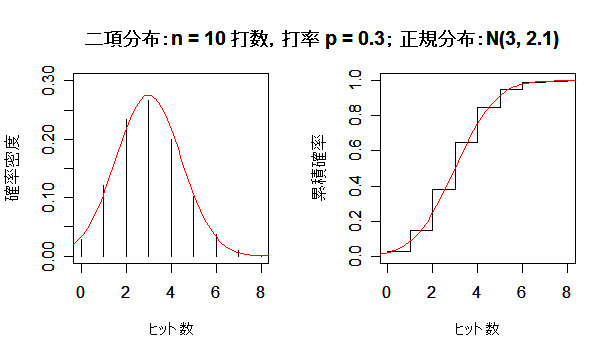
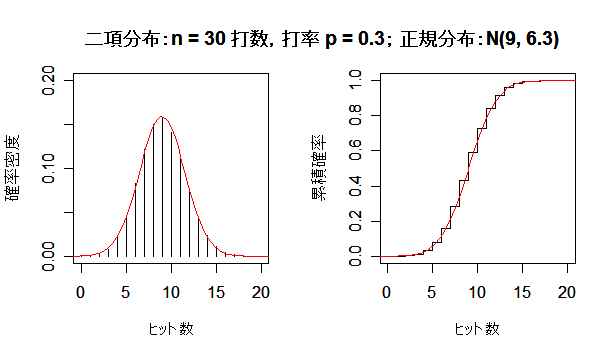
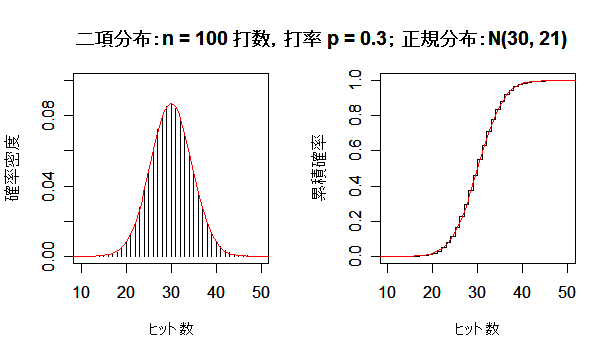
二項分布が正規分布に近づく様子

　成功確率 p の二項分布は，試行回数 n を増やしていくと，平均 np，分散 np(1 - p) の正規分布 に近づく．

6-2．成功確率（比率）の信頼区間

　成功確率 p のベルヌイ試行を n 回行ったとき x 回成功したとすると，成功確率は， p^ = x/n，と推定される．
　成功回数 x は二項分布し，その平均は E[x ] = np，分散は Var[x ] = np(1 - p)，で あるので，成功確率推定量 p^ の平均は E[p^ ] = E[x/n] = p， 分散は Var[p^ ] = Var[x/n] = Var[x ]/n2 = p(1 - p)/n， となる．これより，
binotest
と漸近的に分布するので，標準正規分布の 97.5％点の z0 = 1.96 を用いると， 近似的に
binotest
という不等式が成り立つ．これを整理すると，
binotest
という p の２次不等式を解くことに帰着する．いま，p の２次方程式の根を
binotest
とすると，この根を用い，p の 95％信頼区間は近似的に
binotest
となる．

　試行回数 n が十分大きいと思われるときは，さらに近似を加え， 成功確率推定量 p^ の分散において，真の成功確率 p の 代わりにその推定量 p^ に置き換えて，Var[p^ ] = p^(1 - p^)/n，とみなすと， p の 近似的な 95％信頼区間は，

binotest
と簡略化される．
　簡略化された信頼区間で連続性の補正を入れるには，
binotest
として，信頼区間の幅を拡げる．

　ところで，正規近似による信頼区間の構成では，場合により信頼区間が負になったり 1 を超えることがあるが， このときは，0 と 1 で切り詰める．

例題（テレビ視聴率）
テレビ視聴率は，視聴率の高い番組ほど多くの視聴者が見ているので，広告宣伝の効果が高く影響力が 強いと考えられている．このため，視聴率の高さが広告宣伝費用に反映されるので，テレビ会社は高い視聴率を 得ようとして番組を製作している．
ある調査会社のデータによると，関東地区では 600 世帯を対象にしているようである． NHK 大河ドラマの関東地区世帯視聴率は26.2％であった． 真の世帯視聴率の 95 ％信頼区間を求めよ．
解答：
p の分散推定値は s2 = p^(1 - p^)/n = 0.262*(1 - 0.262)/600 = 0.262*0.738/600 = 0.00032226
p の標準偏差の推定値（標準誤差）は s = √0.00032226 = 0.01795
95 ％信頼区間の幅は d = z0s = 1.96*0.01795 = 0.035
下限は，p^ - d = 0.262 - 0.035 = 0.227， 上限は，p^ + d = 0.262 + 0.035 = 0.297
よって，0.227 < p < 0.297 である．

6-3．成功確率（比率）の検定

標準正規分布による近似検定（大標本理論）

　成功確率 p のベルヌイ試行を n 回行ったときの成功回数 X は， X 〜 B(n, p)，のように２項分布に従う．X の平均と分散はそれぞれ， E[X ] = np，Var[X ] = np(1 - p)，である．
　ここで，成功確率が p0 であるという帰無仮説，
H0： p = p0
の検定を考える．帰無仮説のもとでは，成功回数 X は，X 〜 B(n, p0)， と分布するので，X をその平均と標準偏差で標準化すると，中心極限定理から，
binotest
のように標準正規分布に漸近的に従う．
　これより，近似的な 5％両側検定は，標準正規分布の 97.5％分位点の z0 = 1.96 より 検定統計量 T = |z| の値が大きくなったとき帰無仮説を棄却するこへとで得られる． なお，二項分布は離散的なので，イエーツの連続性の補正を行った検定統計量を用い，
binotest
のとき帰無仮説を棄却する方が近似の精度がよいと言われている．

例題
A 君と B 君が将棋を行った．10 局やったところ，A 君の 7 勝 3 敗であった．A 君と B 君で将棋の強さに 違いがあるか検定せよ．また，30 局やって，A 君の 21 勝 9 敗であったとき（勝率は 7 割で先ほどと同じ） ではどうか．
解答
帰無仮説として，A 君と B 君の将棋の強さが等しい，とする．すなわち，A 君の勝率が 0.5 であるとする． よって，
H0： p ＝ 0.5
である．
平均：m = np = 10*0.5 = 5，分散：s2 = np(1 - p) = 10*0.5*0.5 = 2.5
z = (X - m)/s = (7 - 5)/√2.5 = 1.265
検定統計量 |z| = 1.265 < 1.96（標準正規分布両側 5 ％有意水準）なので，帰無仮説は棄却されない． すなわち，A 君と B 君の将棋の強さは同じと考えてもよい．
30 局のときは， 平均：m = np = 30*0.5 = 15，分散：s2 = np(1 - p) = 30*0.5*0.5 = 7.5
z = (X - m)/s = (21 - 15)/√7.5 = 2.19
1.96 < 2.19 < 2.58（標準正規分布両側 1 ％有意水準）なので，帰無仮説は有意水準 5 ％で棄却される． すなわち，A 君と B 君の将棋の強さは同じでないと考えられる．
Copyright (C) 2008, Hiroshi Omori. 最終更新：2008年10月 2日