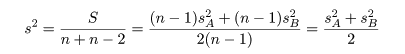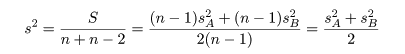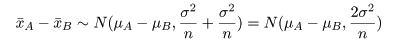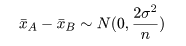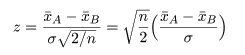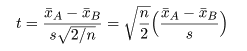2008.12.4

お待たせしました．講義プリントサイトをアップしました．
http://lbm.ab.a.u-tokyo.ac.jp/~omori/kokusai/koki.htm

8-5. 2 つの母集団平均に対する t 検定（サンプルサイズが等しいとき）

　前節の 2 つの母集団平均に対する t 検定は，2 つの母集団から抽出した標本の大きさが ともに等しい n であるときは，計算がずっと簡単になる．先ほどと同様に，

帰無仮説，H0： μA ＝ μB
対立仮説，H1： μA ≠ μB

とする．

母集団 A と B からそれぞれ大きさ n の標本を抽出した． 母集団 A からの標本の標本平均が x-A， 標本分散が sA2 であり，母集団 B の 標本平均が x-B， 標本分散が sB2 であった．母集団 A，B が共通の 分散 σ2 をもつとすると，その推定値 s2 は 以下のように推定できる．

母集団 A からの標本の偏差平方和： 　SA＝（n - 1）sA2
母集団 B からの標本の偏差平方和： 　SB＝（n - 1）sB2
母集団 A，B 全体での偏差平方和： 　S ＝ SA ＋ SB ＝（n - 1）sA2＋ （n - 1）sB2
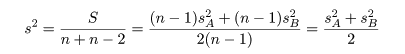
母集団 A，B 共通の標本分散： bunsan

また，母集団Aの標本分布は，N（μA，σ2）であり，母集団Bでは， N（μB，σ2）であることから，それぞれの標本平均は，
x-A 〜 N（μA，σ2/n）， x-B 〜 N（μB，σ2/n）
と分布する．これより，標本平均の差x-A− x-Bは，
diffmean
と分布する．

帰無仮説（H0： μA ＝ μB）のもとでは，μA−μB＝0，なので， 標本平均の差は，

diffmean
と分布する．これを標準化した z 値，
diffz
において，標準偏差 σ の代わりに標本標準偏差 s を代入した t 値，
difft
が自由度 n + n - 2 = 2n - 2 の t 分布に従うことを利用して検定ができる．
例題
　あるダイエット食品の効果を調べるため，ダイエット食品の摂取群10名と通常食事群10名に 被験者をランダムに分けて，3ヶ月間実験を行った．３ヶ月での体重減少量は， ダイエット食摂取群（Ｄ群）で平均2.3kg，標準偏差2.0kgであり，通常食事群（N群）で平均0.5kg， 標準偏差1.2kgであった．ダイエット食品には効果が認められるかの検定を上の表の数値を用いて行う．
　Ｄ群とＮ群では，標準偏差にそれほど違いがあるとは思われなかったので， Ｄ群とＮ群は共通の標準偏差σを持つと仮定した．
解答例
ダイエット食摂取群（Ｄ群）の体重減少量の母集団平均を μD とおき， 通常食事群（N群）の体重減少量の 母集団平均を μN とおく．
この問題での帰無仮説（H0）と対立仮説（H1）は，
H0： μD ＝ μN
H1：μD ≠ μN
と定式化される．以下の表を埋めて解答する．
Copyright (C) 2008, Hiroshi Omori. 最終更新：2008年12月4日