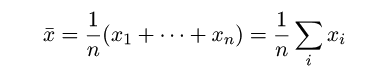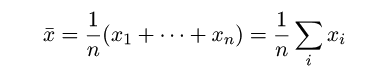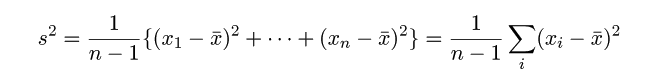2008.4.24

携帯解答サイト： http://lbm.ab.a.u-tokyo.ac.jp/~omori/k/

問８の先週の回答結果

選択肢	１	２	３	４	計
回答者数	2	10	5	2	19

　

回答総数が少なかった．回答分布もあまり変わらなかった．

　

問９．問８の回答の理由を掲示板に投稿せよ．

先週の投稿例

• （大学生に）漢検を受けるのを義務づける
• 調べたらこのような結果が出たのでしょうがない．
• 新入社員は，入社試験や資格を増やすために勉強するので少しは出来るようになっている．
• 他の対象と同じ条件で調査が行われていないと思った．
• 試験内容や対象者が統一されていないから．
• 高校の時は漢字テストがあったから多少勉強していたが，大学では漢字テストがないし，自分でも 高校の時より漢字がすぐ出て来なくなった気がするから．

　

問10．どのような試験を行えば大学生の漢字能力がより明瞭にわかるか．掲示板に投稿せよ．

先週の投稿例

• 大学生が中学，高校のレベルの問題を解いて，その結果次第で白黒がつく．
• 大学生だけでなく，同年代の人全てを対象にして試験を行う．

　

ヒストグラムに対する先週の回答結果

選択肢	１	２	３	４	計
回答者数	0	9	12	0	21

　

今週は回答総数が少なかった．２か３のどちらが良いかで意見が割れた．ヒストグラムは分布の山の数，対称性， 異常値の有無などを視覚的に表現するもので，英語得点分布表示は３がやや良いような気がする．

　

回答の理由を投稿せよ．

先週の投稿例

• 階級幅10が一番見た目にもスマートで，推移の様子も分かりやすい．
• 線が少ない方がみやすい．
• おおざっぱすぎず細かすぎないから３．
• 10点ごとに区切られていて，何点台の人が多いのか一目でわかるから．
• １だと20の内の数がわからない．２も同様．４は細かすぎて見づらい．３なら，５ずつに分かれていて， 日本人の心理なら許容範囲だと思うから．
• ５点ずつというのが，見やすく，パッと見て分かりやすいから．

４. 量的データの代表値

4-1．データと統計量

4-2．データの中心的な位置を表す統計量

（標本）平均：x^-

例題１

A さんの 5 教科のテスト得点は，国語 65 点，数学 30 点，英語 50 点， 社会 55 点，理科 35 点であった．平均得点を求めよ．

　

解答例：x^- = (65＋30＋50＋55＋35)/5 = 235／5 ＝ 47，−＞答：47点

中央値（メディアン）

例題２

A さんのテスト得点の中央値を求めよ．

　

解答例：得点を小さい順に並べると，30，35，50，55，65，である．真ん中は50．−＞答：50点
注）国，数，英，社の4教科のメディアンは，小さい順に並べて，30，50，55，65，となる． 真ん中の値がないので，その両側の値50と55の平均値52.5とする．

最頻値（モード）

• １世帯あたり平均貯蓄額
  
  総務省統計局の調査によると，平成16年１世帯あたりの平均貯蓄額は平均1,692万円であった． A さんの家庭の貯蓄額は1,200万円であった．以下の選択肢からそう思われるものを選び，携帯で送信せよ．

  問１：日本の全国の世帯を「金持ち」，「貧乏」の２つのカテゴリーに等分したとすると，A さんはどれに属すると 思いますか．選択肢解答テスト第１問で送信せよ．

  １．絶対に金持ち

  ２．多分金持ち

  ３．多分貧乏

  ４．絶対に貧乏

  　

  問２：日本の全国の世帯を「金持ち」，「普通」，「貧乏」の３つのカテゴリー に３等分したとすると，平均貯蓄額1,692万円を持っている世帯はどのカケゴリーに属すると思いますか． 選択肢解答テスト第２問で送信せよ．

  １．金持ち

  ２．普通

  ３．貧乏

  　

  上の回答の理由を掲示板に投稿せよ．

4-3．データのちらばりの程度を表す統計量

（標本）分散： s²

標準偏差（SD，Standard Deviation）： s

例題３

以下の木材の長さデータ（cm）の標本分散と標準偏差を求めよ．

2，3，5，8

　

解答例：データの平均値は，x^-＝（2＋3＋5＋8）／4 ＝ 18／4 ＝ 4.5cm

データ	2	3	5	8
偏差	-2.5	-1.5	0.5	3.5
偏差平方	6.25	2.25	0.25	12.25

偏差平方和：S＝��_i(x_i−x^-)² ＝6.25＋2.25＋0.25＋12.25＝21
標本分散：s²＝21／(4-1)＝ 7cm²，標準偏差(SD)：s＝√7＝ 2.65cm

最大値，最小値

分位点（パーセンタイル）

• 25％点：全データの下位25％が入る点 　　　
• 50％点（中央値）：全データの下位50％が入る点 　　　
• 75％点：全データの下位75％が入る点

四分位範囲

箱ひげ図（ボックスプロット）

• 平均値，標本分散の計算
  以下のデータの代表値を小数第１位まで（小数第２位まで求めて四捨五入する）求めよ． 計算には電卓等を用いてよい．解答は数値解答テストで送信(半角数字) すること．
  9，4，6，5，-4，2，-1, 3
  第１問：メディアン（中央値）
  第２問：平均値
  第３問：標本分散
  第５問：標準偏差（SD）

  計算用紙
  

  データ	9	4	6	5	-4	2	-1	3
  偏差
  偏差平方