2008.5.15
携帯解答サイト: http://lbm.ab.a.u-tokyo.ac.jp/~omori/k/
- 平均値,標本分散の計算(再挑戦)の結果
-
第1問:メディアン
| 内訳 |
解答者数 | 間違い |
正解 | のべ解答数 |
|---|
| 人数 |
26 | 12 |
27 | 39 |
-
-
第2問:平均
| 内訳 |
解答者数 | 間違い |
正解 | のべ解答数 |
|---|
| 人数 |
24 | 16 |
25 | 41 |
-
-
第3問:標本分散
| 内訳 |
解答者数 | 間違い |
正解 | のべ解答数 |
|---|
| 人数 |
23 | 32 |
19 | 51 |
-
-
第4問:標本標準偏差
| 内訳 |
解答者数 | 間違い |
正解 | のべ解答数 |
|---|
| 人数 |
18 | 19 |
15 | 35 |
-
-
前回より成績が向上してよかった.
5-2.正規分布の形状
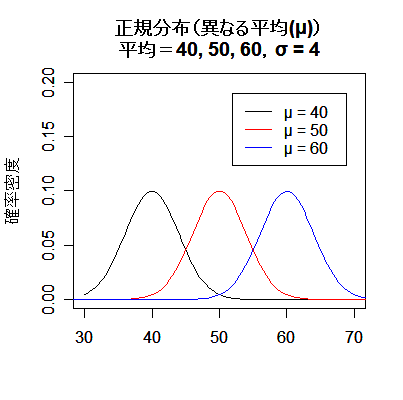
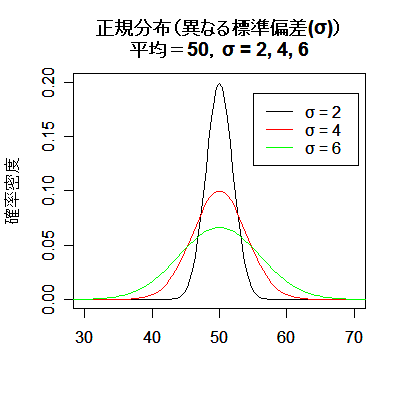
平均 μ と分散 σ2(標準偏差 σ)の違いにより分布の形状がどのように異なるかをみてみよう.
左下図をみると,平均 μ は分布の中心的な位置を表している.また右下図をみると,標準偏差 σ は分布の拡がりを表している.
すなわち,σ が小さいと分布はより平均の近くに集まり,σ が大きいと分布は幅広い範囲に拡がる.
正規分布は,数量データの分布を表す最も重要な分布である.そのわけは,
- 身長,体重など正規分布に従うデータが多い(経験的知識)
- どのような分布をもつ母集団からのサンプルであっても,データの平均値はデータ
数を増やせば正規分布に近づく(中心極限定理)
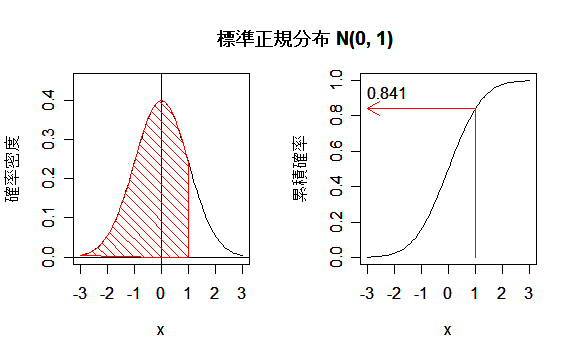
5-3.標準正規分布 N(0, 1)
平均 μ = 0,分散 σ2 = 1(標準偏差も1)の正規分布を標準正規分布という.
正規分布との関係
-
| 正規分布 |
標準正規分布 |
| 平均:μ,分散:σ2
|
平均:0,分散:1 |
| x 〜
N( μ,σ2 ) |
z 〜 N(0,1) |
| z = (x − μ)/σ |
x = μ + σ*z
|
|
標準正規分布累積確率表
| z の値 |
0.0 | 0.1 | 0.2 |
0.3 | 0.4 | 0.5 |
0.6 | 0.7 | 0.8 |
0.9 | 1.0 |
| 累積確率 |
0.500 | 0.540 | 0.579 |
0.618 | 0.655 | 0.691 |
0.726 | 0.758 | 0.788 |
0.816 | 0.841 |
| 1.1 | 1.2 |
1.3 | 1.4 | 1.5 |
1.6 |
1.64 |
1.7 | 1.8 |
1.9 | 1.96 |
2.0 | 2.58 |
3.0 |
| 0.864 | 0.885 |
0.903 | 0.919 | 0.933 |
0.945 |
0.95 |
0.955 | 0.964 |
0.971 | 0.975 |
0.977 | 0.995 |
0.999 |
- 標準正規分布累積表の使い方(小数第1位)
以下のデータの代表値を小数第1位まで(小数第2位まで求めて四捨五入する)求めよ.
計算には電卓等を用いてよい.解答は数値解答テストで送信(半角数字)
すること.
第1問:標準正規分布 N(0, 1) で,1以上にデータの何%を含むか.
第2問:標準正規分布で,-2以下にデータの何%を含むか.
第3問:標準正規分布で,-1から1までの間にデータの何%を含むか.
第4問:標準正規分布で,-1.96から1.96までの間にデータの何%を含むか.
第5問:平均50点,標準偏差10点の正規分布 N(50,100) で,50点以下にデータの何%を含むか.
第6問:平均50点,標準偏差10点の正規分布で,35点以上にデータの何%を含むか.
第7問:平均50点,標準偏差10点の正規分布で,上位5%以内に入るには何点(整数)あればよいか.
第8問:1万人が受けたテストの平均は50点,標準偏差は10点であった.70点の学生の順位.
5-4. 独立な正規分布の合成分布
平均 μ1,
分散 σ12,の正規分布
からの標本 x 〜
N( μ1,σ12 )
と,
平均 μ2,
分散 σ22,の正規分布
からの標本 y 〜
N( μ2,σ22 )
があり,両者が互いに独立であるとする.(y の値は x の値の影響を受けない.)
- 和の分布
-
x + y は平均 μ1 +
μ2,分散 σ12 +
σ22,の正規分布に従う.
x + y 〜 N(
μ1 + μ2,
σ12 +
σ22 )
- 差の分布
-
x − y は平均 μ1 −
μ2,分散 σ12 +
σ22,の正規分布に従う.
x − y 〜 N(
μ1 − μ2,
σ12 +
σ22 )
- 一般の線形結合の分布
-
a と b を任意の実数(スカラー)とすると,x と y の線形結合
ax + by は,
ax + by 〜 N(
aμ1 + bμ2,
a2
σ12 +
b2
σ22 )
- 例題
- 平均 μ 分散 σ2 の正規分布から無作為標本
(ランダムサンプル),
x1,
x2,
x3,
を抽出した.標本平均 x- の分布を求めよ.
- 解答例
-
x- = (x1 +
x2 +
x3 )/3 =
(1/3)x1 +
(1/3)x2 +
(1/3)x3,
である.これより,
標本平均 x- の平均:E[x- ] =
(1/3)μ + (1/3)μ + (1/3)μ = μ
標本平均 x- の分散:Var[x- ] =
(1/3)2σ2
+ (1/3)2σ2
+ (1/3)2σ2
= (1/3)σ2
よって,x- 〜 N(μ,σ2/3 ).
標準偏差は σ/√3.
- 正規分布からの標本(サンプル)の平均値の分布
-
平均 μ,分散 σ2 の正規分布から大きさ n の標本を抽出
→ 標本平均 x- は平均 μ,分散 σ2/n
(標準偏差 σ/√n)の正規分布に従う.
x- 〜 N(μ,σ2/n ).
→ 標本の大きさ(サンプルサイズ)を大きくすれば,母集団平均 μ は標本平均 x- で
精度よく推定できる.
Copyright (C) 2008, Hiroshi Omori. 最終更新:2008年 5月15日