2008.5.22
携帯解答サイト: http://lbm.ab.a.u-tokyo.ac.jp/~omori/k/
標準正規分布 N(0,1) 累積表の結果
第1問:1 以上
| 内訳 |
解答者数 | 間違い |
正解 | のべ解答数 |
|---|
| 人数 |
27 | 73 |
21 | 94 |
| |
第2問:-2 以下
| 内訳 |
解答者数 | 間違い |
正解 | のべ解答数 |
|---|
| 人数 |
25 | 16 |
20 | 36 |
|
第3問:-1 から 1
| 内訳 |
解答者数 | 間違い |
正解 | のべ解答数 |
|---|
| 人数 |
21 | 7 |
20 | 27 |
| | <
第4問:-1.96 から 1.96
| 内訳 |
解答者数 | 間違い |
正解 | のべ解答数 |
|---|
| 人数 |
19 | 1 |
18 | 19 |
|
標準正規分布累積表の使い方と意味については理解できたようだ.
5-3.標準正規分布 N(0, 1)(追加)
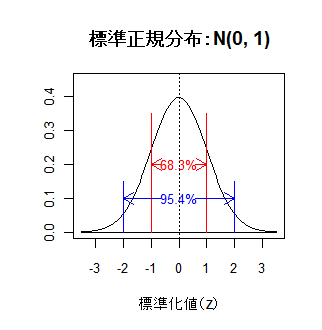
標準正規分布 N(0, 1) では,-1 ≦ z ≦ 1 の範囲に全体の68.3%が含まれ,
-2 ≦ z ≦ 2 の範囲に全体の95.4%が含まれる(下左図).
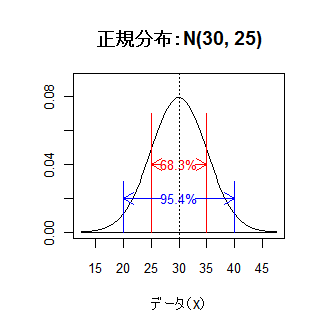
また,平均 μ - 30,
分散 25 の正規分布 N(30, 25) では,標準偏差が σ = √25 = 5 なので,
25 ≦ x ≦ 35 の範囲に全体の68.3%が含まれ,
20 ≦ x ≦ 40 の範囲に全体の95.4%が含まれる(下右図).
範囲に含まれる確率
| N(0, 1) |
N(30, 25) |
N(μ,σ2) |
確率(%) |
| -1 → 1 |
25 → 35 |
μ - σ → μ + σ |
68.3 |
| -1.96 → 1.96 |
20.2 → 39.8 |
μ - 1.96σ → μ + 1.96σ |
95.0 |
| -2 → 2 |
20 → 40 |
μ - 2σ → μ + 2σ |
95.4 |
| -2.58 → 2.58 |
17.1 → 42.9 |
μ - 2.58σ → μ + 2.58σ |
99.0 |
| -3 → 3 |
15 → 45 |
μ - 3σ → μ + 3σ |
99.7 |
- 例題
-
標準正規分布では,-2から2までの間に全データのかなりの部分(95.4%)が含まれる.
平均 8,分散 4 の正規分布でこの区間に対応するのは何か.
-
平均μ=8,標準偏差σ=√4=2.
小さい値=μ−2σ=8−2*2=4,
大きい値=μ+2σ=8+2*2=12.
これより,4 〜 12,に全データのかなりの部分が含まれる.
第9問:1000人の学生による英語試験の成績は,平均60点,標準偏差は12点であった.
上位30番以内に入るには何点が必要か.(携帯で送信)
5-4. 独立な正規分布の合成分布(続き)
- 例題
-
平均身長 172.5cm,標準偏差 6cm の集団 A と,平均身長 168cm,標準偏差 4.5cm の集団 B がある.
いま,集団 A,B からそれぞれ 1 人をランダムに選んだとき,集団 A から選ばれた人の方が集団 B から
選ばれた人より背が高くなる確率を求めよ.
- 解答例
-
集団 A からの標本を x,集団 B からの標本を y とする.
x 〜 N(172.5,36),y 〜 N(168,20.25)なので,
u = x − y 〜 N(4.5,56.25)に従う.
つまり,
集団 A からの標本と集団 B からの標本の差は,平均 4.5cm,標準偏差 √56.25=7.5cm の
正規分布に従う.この正規分布が 0 より大きくなる確率を求めればよい.
標準正規分布に変換すると,
z = (u − μ)/σ = (0−4.5)/7.5 = -0.6
となるので,標準正規分布が -0.6 以上となる確率である.正規分布の対称性から,
Pr[ z > -0.6 ] = Pr[ z < 0.6 ] = 0.726
である.
- 例題
-
上記の 2 つの集団 A,B において,こんどは両集団からそれぞれランダムに 9 名ずつ選び,それぞれの
平均身長を計算した.集団 A から選ばれた人の平均身長の方が集団 B から
選ばれた人の平均身長より高くなる確率を求めよ.
- 解答例
-
集団 A からの標本を x1 ,…,
x9,
集団 B からの標本を y1 ,…,
y9,とし,それぞれの平均を x-,
y- とする.
xi 〜 N(172.5,36)より
x- 〜 N(172.5,36/9)=N(172.5,4),同様に,
yi 〜 N(168,20.25)より
y- 〜 N(168,2.25)である.
これより,集団 A,B の平均身長の差は,
u = x- − y- 〜 N(4.5,6.25)と分布する.
すなわち,
集団 A,B の標本平均の差は,平均 4.5cm,標準偏差 √6.25=2.5cm の正規分布に従う.
この正規分布が 0 より大きくなる確率を求めればよい.
標準正規分布に変換すると,
z = (u − μ)/σ = (0−4.5)/2.5 = -1.8
となるので,標準正規分布が -1.8 以上となる確率である.正規分布の対称性から,
Pr[ z > -1.8 ] = Pr[ z < 1.8 ] = 0.964
である.