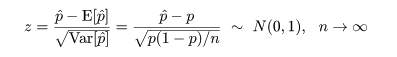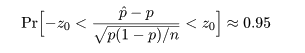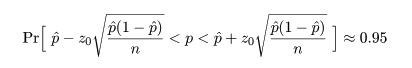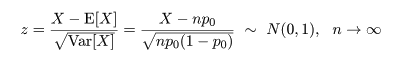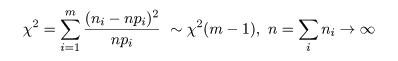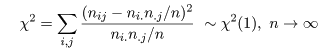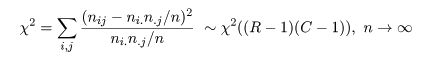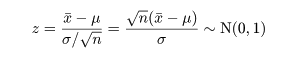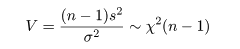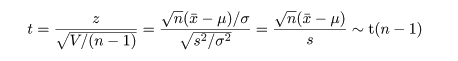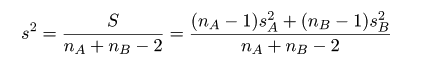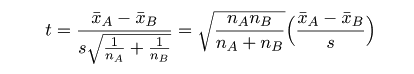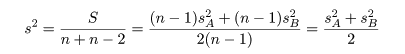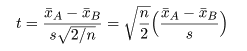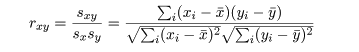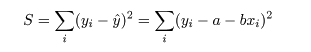2009. 1.15

講義プリントサイト：http://lbm.ab.a.u-tokyo.ac.jp/~omori/kokusai/koki.htm
冬休みの課題：提出者は後期得点が 10 点アップする．
注）３番目の課題ですが， 頭の0を抜かした番号を入力してやって下さい．
それ以外の番号を入力した人(3人)はお手数ですがもう一度やって下さい．

後期の復習

二項分布

成功確率 p の事象を n 回試行したときの成功回数 r の分布．
r 〜 B(n, p) と書く．
平均：np，分散：np(1 - p)
試行回数 n を増やしていくと，平均 np，分散 np(1 - p) の正規分布に近づく．

比率の信頼区間

n 回行って X 回成功したとすると，成功確率 p は， p^{^} = X/n，と推定．
p^{^} の平均：E[p^{^} ] = p， 分散：Var[p^{^} ] = p(1 - p)/n

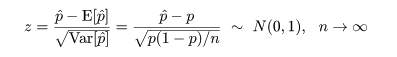
標準正規分布の 97.5％点： z₀ = 1.96 を用い，p の 95％信頼区間は，

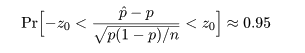
これを解いて，簡略化すると，

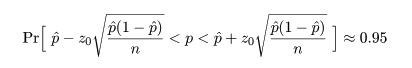
比率の検定

帰無仮説，H₀： 成功確率（比率） p = p₀
n 回行って X 回成功

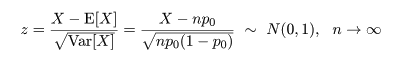
近似的な有意水準 5％両側検定：|z| ＞ z₀ = 1.96 のとき帰無仮説を棄却

χ² 分布（カイ２乗分布）

標準正規分布の２乗の分布： z_i 〜 N(0, 1) → z_i² 〜 χ² (1) ，自由度 1 の χ² 分布
標準正規分布 n 個の２乗和の分布： X_n ＝ z₁²＋ … ＋ z_n² 〜 χ² (n)，自由度 n の χ² 分布

ピアソンの χ² 値

適合度検定

想定離散分布 p_i，観測度数 n_i
帰無仮説 H₀：データは想定確率分布に従う．

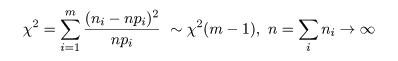
2×2 分割表

比率の同等性の検定： 帰無仮説，H₀： p_x ＝ p_y， 対立仮説，H₁： p_x ≠ p_y
独立性の検定： 帰無仮説，H₀： p_ij ＝ p_i.p_.j， 対立仮説，H₁： p_ij ≠ p_i.p_.j
ピアソンの χ² 値を，自由度 1 の χ² 分布で検定．つまり，

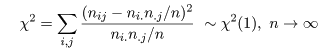
オッズ比：関連性の強さを表す指標．帰無仮説，H₀：オッズ比 = 1

R×C 分割表

帰無仮説，H₀： p_ij ＝ p_i.p_.j， 対立仮説，H₁： p_ij ≠ p_i.p_.j
ピアソンの χ² 値を，自由度 (R - 1)(C - 1) の χ² 分布で 検定．つまり，

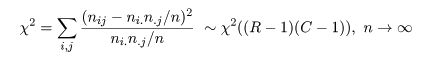
t 分布

標準正規分布に従う確率変数を z，(z 〜 N(0,1))， 自由度 n の χ² 分布に従う 確率変数を V，(V 〜 χ²(n))，

n 個のデータが x_i 〜 N( μ，σ² ) のとき， 標本平均： x^-，標本分散： s²

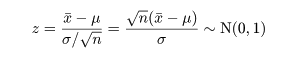
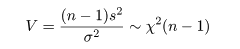
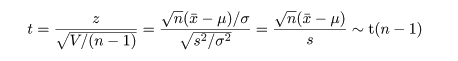
分散未知のときの母平均 μ の 95％ 信頼区間

自由度 n − 1 の t 分布の 97.5％分位点 t₀ と すると，
Pr[ x^- − t₀ s / √n ＜ μ ＜ x^- ＋ t₀ s / √n　] ＝ 0.95

母平均に対する t 検定

帰無仮説 H₀：μ ＝ μ₀， 対立仮説 H₁：μ ≠ μ₀，
検定統計量 t 値：t ＝ √n ( x^- − μ₀ )/s，
自由度 n−1 の t 分布表で検定

2 つの母集団平均に対する t 検定

帰無仮説，H₀： μ_A ＝ μ_B，対立仮説，H₁： μ_A ≠ μ_B
母集団 A ：n_A 個の標本，標本平均 x^-_A， 標本分散 s_A²
母集団 B ：n_B 個の標本，標本平均 x^-_B， 標本分散 s_B²

母集団 A，B 共通の標本分散：

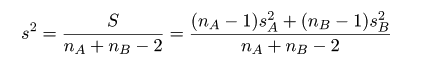
検定統計量 t 値：：

自由度 n_A＋n_B−2 の t 分布表で検定

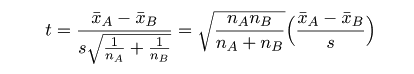
2 つの母集団平均に対する t 検定（サンプルサイズが等しいとき）

n_A = n_B = n

母集団 A，B 共通の標本分散：

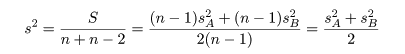
検定統計量 t 値：

自由度 自由度 n + n - 2 = 2n - 2 の t 分布表で検定

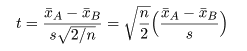
共分散

Cov(x ，y ）＝ s_xy ＝ （1/n−1）Σ_i （x _i − x^- ） （y _i − y^- ）

相関係数

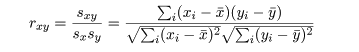
-1≦r≦1，r が 1 に近いと正の相関関係，-1 に近いと負の相関関係，0 に近いと線形的な関係なし．

直線回帰

変数 y ：従属変数，目的変数，変数 x ：独立変数，説明変数
y ＝ a ＋ b x，a：y 切片，b：回帰係数

最小２乗法による回帰係数の推定

データ点 （x_i ，y_i ）， 回帰による推定点， （x_i ，y^_i ）， i = 1，…，n，との距離の２乗

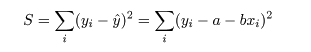
を最小化すると，その解は，

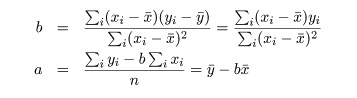
この平方和 S の最小値が残差平方和 S_e，回帰係数の推定値を a^，b^

残差分散

自由度 n - 2， s_e² ＝ S_e/(n−2) ＝ Σ_i（y_i −　 y_i^ ）² /(n−2)

回帰係数 b の分散

s_b² ＝ s_e²/Σ_i （x _i − x^- ) ²

回帰関係の検定

帰無仮説，変数 y は変数 x との回帰関係にない．H₀：b ＝ 0
検定統計量 t 値：t ＝ b^/s _b，自由度 n−2 の t 分布で検定

回帰関係の 95％ 信頼区間

自由度 n−2 の t 分布の 97.5％点を t₀， b^ − t₀ s _b ＜ b ＜ b^ ＋ t₀ s _b

平方和分解

Σ_i（y _i − y^- ) ² ＝ Σ_i （y^_i − y^- ) ² ＋ Σ_i （y _i − y^_i ) ²
S_T ＝ S_R ＋ S_e， 総平方和 ＝ 回帰平方和 ＋ 残差平方和

決定係数（重相関係数の２乗）

R² = S_R / S_e ＝（回帰平方和）/（総平方和），　総平方和のうち回帰平方和で説明される割合，大きい程よい．

分散分析

回帰分析の分散分析表

変動因	平方和	自由度	平均平方	F 値
回帰	SR	1	SR	F ＝ SR/se2
残差	Se	n−2	se2 ＝ Se/n−2
全体	ST	n−1

F 値が大きい程，回帰関係が有意となる．F 値は回帰係数の t 値の２乗．