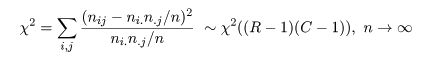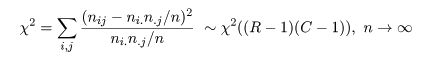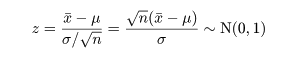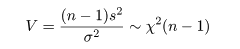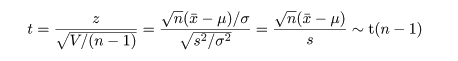2009.10.29
9-4.R × C 表
大きさ n の標本を2つの変数 A,B で分類したとき,2つの変数に関連があるかを調べたい.
変数 A が R 個のカテゴリー A1, A2,…,AR,に分かれ,
変数 B が C 個のカテゴリー B1, B2,…,BC,に分かれていると
すると,標本のうち,カテゴリー Ai,Bj に落ちた個数を
nij とすると,以下のようび R × C 表にクロス集計される.
R × C 分割表データ
| | B1 | B2 |
… | BC | 計 |
|---|
| A1 | n11 |
n12 |
… |
n1C |
n1・ |
|---|
| A2 | n21 |
n22 |
… |
n2C |
n2・ |
|---|
| : | : |
: | … |
: | : |
|---|
| AR | nR1 |
nR2 |
… |
nRC |
nR・ |
|---|
| 計 | n・1 |
n・2 |
… |
n.C |
n |
|---|
すると,2 × 2 分割表のときと同様に,
集団 i の標本の中で,反応 j を取る確率を pij とし,集団 i の周辺確率を pi.,
反応 j の周辺確率を p.j とすると,独立性の仮説は,
帰無仮説,H0: pij = pi.p.j,
対立仮説,H1: pij ≠ pi.p.j,
の検定になる.帰無仮説のもとで χ2 値が,
と分布するので,独立性の検定や頻度分布の同等性の検定を行うことができる.
- 例題
-
カップヌードルの好みは年代によって違いがあるかどうかを調べた.10代,20代,30代,40代
の被験者をそれぞれ100名ずつ選び,好みを聞いたところ以下の表がえられた.
帰無仮説 H0:ヌードルの好みは年代により異ならない
の検定を行え.
年代による好みの違い
| | 10代 | 20代 | 30代 |
40代 | 計 |
|---|
| カップヌードル | 41 | 50 |
57 | 56 | 204 |
|---|
| シーフードヌードル | 59 | 50 |
43 | 44 | 196 |
|---|
| 計 | 100 | 100 |
100 | 100 |
400 |
|---|
-
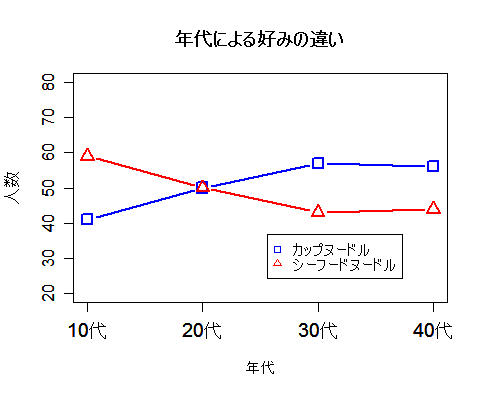
グラフに図示すると以下のようになった. 若い人(10代)はシーフードヌードルを好み,
比較的年配の人(30代,40代)はカップヌードルを好む傾向にありそうに見える.
- 解答
-
表から,観測度数,期待度数,偏差を計算し,ピアソンの χ2 値を計算する.
自由度 (2 - 1)×(4 - 1) = 3 の χ2 分布表から有意かどうか判定する.
- 30代と40代では,好みに違いがなさそうなので,検定の自由度を減らすため,30代と40代でまとめて,
10代,20代,30・40代の3つのカテゴリーにまとめてみた.この場合の自由度は
(2 - 1)×(3 - 1) = 2 となり,自由度が一つ減って有意になりやすくなる.
年代による好みの違い2
| | 10代 | 20代 | 30-40代 |
計 |
|---|
| カップヌードル | 41 | 50 |
113 | 204 |
|---|
| シーフードヌードル | 59 | 50 |
87 | 196 |
|---|
| 計 | 100 | 100 |
200 |
400 |
|---|
10.t 検定
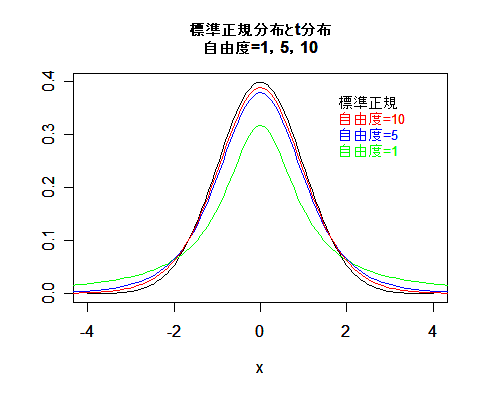
10-1. t 分布
定義
標準正規分布に従う確率変数を z,(z 〜 N(0,1)),
自由度 n の χ2 分布に従う
確率変数を V,(V 〜 χ2(n)),
とする.
両者が独立であるとすると,その比 t は,自由度 n の t 分布,t(n),に従う.
分散未知のときの標本平均の分布
正規母集団 N( μ,σ2 ) から大きさ n の
標本を取り出したとき,標本平均 x- を標準化したもの z は,
と標準正規分布に従う.
母標準偏差 σ が未知であるときこれを標本標準偏差 s で置き換えた
ものを t 値といい,自由度 n − 1 の t 分布に従う.
これは,標本分散の分布から
であるので,比を取ると,
となるからである.
Copyright (C) 2008, Hiroshi Omori. 最終更新:2009年10月29日