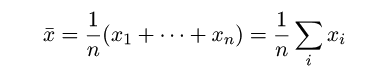2009.4.23
東京国際大学
統計学の基礎
- テーマパークの利用状況に対する先週の回答結果
-
| 選択肢 |
1 | 2 |
3 | 4 |
5 | 計 |
|---|
| 問1:東京ディズニーランド |
39 | 36 |
11 | 1 |
7 | 94 |
| 問2:東京ドームシティ |
7 | 16 |
20 | 7 |
35 | 85 |
| 問3:八景島シーパラダイス |
1 | 9 |
24 | 18 |
27 | 79 |
| 問4:ナムコ・ナンジャタウン |
9 | 14 |
18 | 11 |
25 | 77 |
表にしてまとめると,テーマパーク個別にみるよりは,利用度の違いがわかりやすくなる.
さらに,下図のようにグラフにするとより分かりやすい.
回答者総数に違いがあるのでグラフがでこぼこして見にくい.そこで百分率にすると,利用度
分布がわかり,テーマパークによる利用度の違いがより明瞭になる.
上図をみると,ディズニーランドはリピーターの割合が40%もあり,学生に非常に支持されている.
また,ディズニーランドに興味がない学生もあまりいないことがわかる.
これに対し,シーパラダイスは,ここから遠いせいもあるかも知れないが,リピーターの割合が非常に少なく,
一度行けば十分と思われているようだ.
一方,ドームシティとナンジャタウンの利用度分布は似ていて,一部にコアな利用者がいるが,かなりの
学生からは無視されているようだ.
設問
テーマパークの利用度調査データのまとめ方についての意見や感想を掲示板に投稿せよ.
- 問5の先週の回答結果
-
| 選択肢 |
1 | 2 |
3 | 4 |
5 | 計 |
|---|
| 回答者数 |
6 | 9 |
8 | 5 |
8 | 36 |
-
- 先週の投稿例
-
- 学び残しがあるまま大学生になっているというのには賛同しますが,中学から学びなおす高校もあるくらい
だから追いつかないでしょう.
- 本当に調べたいならば全ての大学から,成績上位層中堅層下位層から選んだうえで試験させるべきです.
- 39.8という数値が漢字検定でのみの数値であることにも不信感があります.
- 無作為という手段に問題があります.たまたま苦手な方ばかりだったのかも知れません.偏りがちな手法
です.
- 何故簡単な漢字を平仮名にすることがあるのかと普通に暮らしていて思います.読めないだろから平仮名
にするのでは悪循環を産んでいます.
- 共同通信社の主張には納得がいきません.漢字は学ぶものでなく日常で覚えるもの.社会側の読ませるという
努力が足らないのだと思います.
- 漢字が苦手だと決めつけすぎてしまっているかもしれないが携帯ばかり使ってるのでは主張に納得するかも
知れない.
- 携帯やパソコンで簡単に変換できちゃうから書く能力が落ちているんじゃないか.
- 自分は漢字書けないし読めないので(共同通信社の主張は)否めない.
- 無作為抽出だからこそ平均値が出て説得力があると考える.
- 大学のレベル別に同じ人数で,漢字検定2級を受けてもらう.
- 中学生と高校生等みんな同じ試験内容にすべき.そこで統計を取った方がいい.
-
2. 質的データと量的データ
統計学で取り扱う値は,変数という考え方で分類できる.
2-1. 変数
質的変数
- 順序なしカテゴリー:
性別(男女),職業(公務員,会社員,学生,主婦,無職など)
- 順位的変数:
成績(優,良,可,不可),嗜好(好き,嫌い),選考(はい,どちらでもない,いいえ)
量的変数
- 離散的(自然数):
世帯数,交通事故数(場合の数がそれほど多くない)
- 連続的(実数):
長さ,身長,重さ,売り上げ(連続的とみなせる)
2-2. 測定
対象に何らかの標識を与える操作(尺度化).データを取ること.
- 名義尺度:
対象をカテゴリーに分ける(順序なしの質的変数に割り付けること)
- 順序尺度:
対象を順序つきのカテゴリー(順位変数)に分けること.
- 間隔尺度:
年次,温度(セ氏)など.数値間の差(引き算)に意味がある.
- 比例尺度:
0が存在する(意味がある).質量(重さ),長さ,価格,絶対温度.
引き算ばかりでなく,比例(割り算)にも意味がある.
3. データのまとめ方
3-1.データ表
収集されたデータは,以下のようにまとめられる.各列が変数を表し,各行が調査や実験対象である標本(サンプル)
を表す.
データ表の例(甘いもの,辛いものは,好き1,嫌い5の5段階評価)
| 標本個体 | 性別 | 年齢(才) | 身長(cm) | 体重(kg) | 甘いもの | 辛いもの |
| サンプル1 | 男 | 23 | 172 |
65 | 2 | 3 |
| サンプル2 | 男 | 18 | 180 |
76 | 5 | 5 |
| サンプル3 | 女 | 20 | 160 |
52 | 5 | 1 |
| サンプル4 | 男 | 20 | 169 |
60 | 4 | 4 |
| サンプル5 | 女 | 22 | 158 |
49 | 1 | 1 |
| サンプル6 | 女 | 19 | 163 |
60 | 5 | 1 |
| : | : | : | : |
: | : | : |
設問
- 上のデータ例で,変数「甘いもの」は以下のどの尺度に該当すると思うか.
以下から選び,
選択肢回答テスト第1問に携帯から送信せよ.
-
| 1.名義尺度 |
2.順序尺度 |
3.間隔尺度 |
4.比例尺度 |
3-2.質的データ
カテゴリーごとにサンプル数を集計する.(先週の集計結果)
3-3.量的データ
度数分布表
階級ごとにデータを分類して階級ごとの頻度を計算.結果をヒストグラムで表示.
- あるクラスの英語得点データ
-
36, 70, 56, 68, 76, 60, 50, 63, 62, 42, 64, 60, 50, 68, 71, 67, 50, 65, 67, 57,
72, 64, 61, 66, 46, 80, 46, 51, 59, 32, 55, 65, 65, 52, 57, 64, 23, 57, 53, 54,
38, 71, 57, 69, 77, 61, 51, 64, 63, 43, 65, 61, 51, 69, 72, 68, 53, 66, 68, 58,
73, 65, 62, 67, 47, 81, 47, 52, 59, 33, 56, 66, 67, 52, 58, 65, 24, 58, 54, 55
-
階級幅を20にして度数分布表を作成
| 得点 | 0 - 20 | 21 - 40 | 41 - 60 | 61 - 80 | 81 - 100 |
| 人数 | 0 | 6 | 34 |
39 | 1 |
階級幅を変えてヒストグラムを書いてみると,
設問
- 上のグラフの中で,どれが一番見やすいと思うか.以下から選び,
選択肢回答テスト第2問に携帯から送信せよ.
| 1.階級幅 = 20 |
2.階級幅 = 10 |
3.階級幅 = 5 |
4.階級幅 = 2 |
5.どれも同じ |
-
- 上の回答の理由を掲示板に投稿せよ.
4. 量的データの代表値
4-1.データと統計量
データ数(サンプルサイズ):n
データ値:x1,x2,…,xn
英語得点データでは,n = 80
統計量:データから計算される値
4-2.データの中心的な位置を表す統計量
(標本)平均:x-
- 例題1
-
A さんの 5 教科のテスト得点は,国語 65 点,数学 30 点,英語 50 点,
社会 55 点,理科 35 点であった.平均得点を求めよ.
-
- 解答例:x- = (65+30+50+55+35)/5 = 235/5 = 47,−>答:47点
中央値(メディアン)
データの真ん中の値 −> 奇数:ちょうど真ん中,偶数:真ん中に最も近い2値の平均.
- 例題2
- A さんのテスト得点の中央値を求めよ.
-
- 解答例:得点を小さい順に並べると,30,35,50,55,65,である.真ん中は50.−>答:50点
注)国,数,英,社の4教科のメディアンは,小さい順に並べて,30,50,55,65,となる.
真ん中の値がないので,その両側の値50と55の平均値52.5とする.
最頻値(モード)
ヒストグラムの山(最も頻度の高い階級)
英語得点の5点階級幅ヒストグラムでは61−65点がモードである.
Copyright (C) 2008, Hiroshi Omori. 最終更新:2009年 4月23日