2009.5.07

携帯解答サイト： http://lbm.ab.a.u-tokyo.ac.jp/~omori/k/

第３問の先週の回答結果

選択肢	１：絶対金持ち	２：多分金持ち	３：多分貧乏	４：絶対貧乏	計
回答者数	3	9	5	1	18

　

　回答総数が少なかったが，多分金持ちと考える学生が多かった． 　貯蓄分布をみると単調減少型になっていて，貯蓄の中央値（メディアン）が1018万円なので，1000万円 以上の貯蓄をもつ家庭はどちらかというと「金持ち」に分類される．

　

第４問の先週の回答結果

選択肢	１：金持ち	２：普通	３：貧乏	計
回答者数	7	10	2	19

　

回答総数は少なかった．普通と考える学生が多かったが，金持ちと捉える学生もかなりいた．
　貯蓄分布をより詳細にみると，平均貯蓄額を下回る家庭が約2/3（67.6％）であった．このため， 平均貯蓄額以上の貯蓄を持つ家庭は，「普通」ではなく「金持ち」に分類した方がよいと思われる．

　

平均値，標本分散の計算

    

第１問：メディアン 内訳 　解答者数　 　間違い　 　正解　　 人数 　26 　8 　23		第２問：平均 内訳 　解答者数　 　間違い　 　正解　　 人数 　24 　4 　23
第３問：偏差平方和 内訳 　解答者数　 　間違い　 　正解　　 人数 　21 　19 　17		第４問：標本分散 内訳 　解答者数　 　間違い　 　正解　　 人数 　16 　26 　15
第５問：標準偏差 内訳 　解答者数　 　間違い　 　正解　　 人数 　13 　9 　12

　

送信時刻をみると，連休中に答えてくれた学生がいてよかった．
偏差平方和や分散は，最初間違えた学生が多かったが，何回目かでできるようになってよかった．

例題

英語得点データにおいて，メディアン（中央値）， 四分位範囲，異常値と思われる値を除いた上での最大値，最小値を求め， 箱ひげ図（ボックスプロット）を書け．

　

解答例：英語データを得点順に並べる．

23, 24, 32, 33, 36, 38, 42, 43, 46, 46
47, 47, 50, 50, 50, 51, 51, 51, 52, 52
52, 53, 53, 54, 54, 55, 55, 56, 56, 57
57, 57, 57, 58, 58, 58, 59, 59, 60, 60
61, 61, 61, 62, 62, 63, 63, 64, 64, 64
64, 65, 65, 65, 65, 65, 65, 66, 66, 66
67, 67, 67, 67, 68, 68, 68, 68, 69, 69
70, 71, 71, 72, 72, 73, 76, 77, 80, 81

• データ数は，n = 80．
• 中央値（50％点）は，40 番目の 60 点と 41 番目の 61 点の平均の 60.5点．
• 25％点は，20 番目の 52 点と 21 番目の 52 点の平均の 52 点．
• 75％点は，60 番目の 66 点と 61 番目の 67 点の平均の 66.5点．
• 四分位範囲は，25％点の 52 点から 75％点の 66.5 点までの，52 〜 66.5 点．
  四分位範囲にデータの真ん中あたりの半数が含まれる．
• 最大値は，81 点．
• 最小値は，23点であるが，ヒストグラムでみてわかるように，23 点と 24 点は他の集団 と離れているので異常値とみなすと，集団での最小値は 32 点．
• これらの統計量を図示したのが箱ひげ図である．
• なお，平均は x^- = 58.6 点
• 標準偏差 SD = 11.6 点．
• これより，データの真ん中あたりの 2/3 は，
  x^- ± SD = 58.6 ± 11.6 = 47 〜 70.2 点に集まっている．

• 中央値，四分位範囲の計算
  

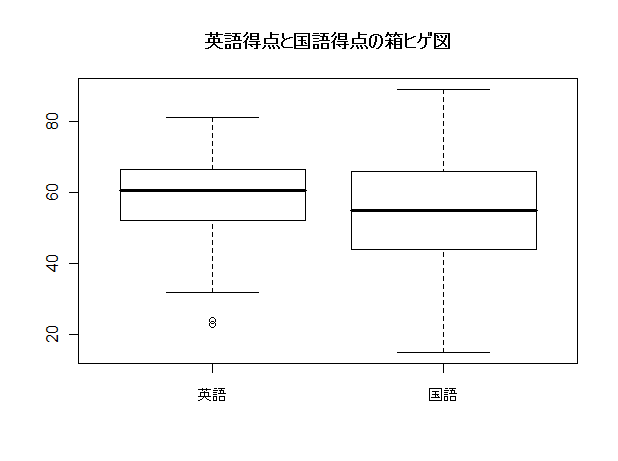
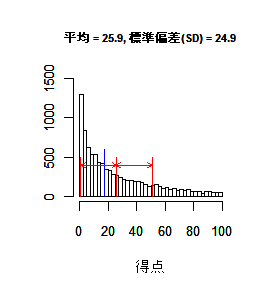
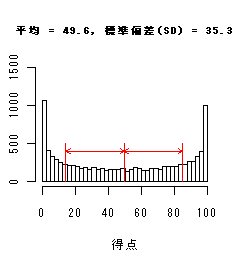
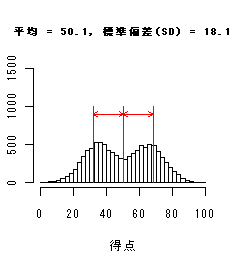
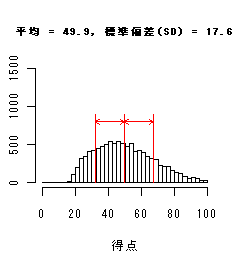
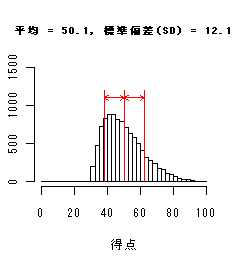
  国語得点データを大きさの順に並べたら以下のようになった． データの代表値を小数第１位まで（小数第２位まで求めて四捨五入する）求めよ． 計算には電卓等を用いてよい．解答は数値解答テストで送信(半角数字) すること．
  　また，これより国語得点の箱ヒゲ図を描け．

  15, 21, 23, 25, 29, 30, 34, 34, 36, 38,
  39, 39, 40, 40, 41, 41, 44, 45, 46, 46,
  47, 47, 49, 50, 50, 52, 52, 53, 53, 54,
  54, 54, 55, 56, 56, 56, 57, 57, 58, 59,
  60, 61, 61, 62, 62, 63, 64, 65, 66, 66,
  67, 68, 68, 70, 70, 71, 72, 73, 75, 76,
  76, 78, 81, 82, 89
  

  第６問：データ数（n）
  第７問：メディアン（中央値）
  第８問：四分位範囲の下限（25％点）
  第９問：四分位範囲の上限（75％点）

  なお，国語データの平均と標準偏差はそれぞれ，
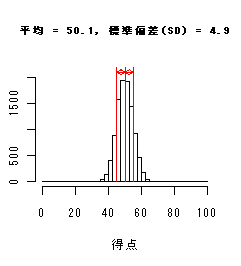
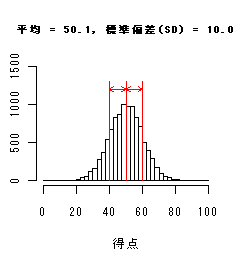
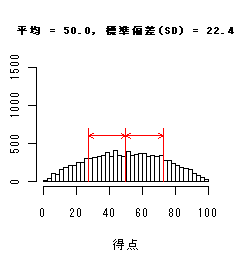
  x^- = 54.2点，SD = 16.0点
  であった．これより，
  x^- ± SD = 54.2 ± 16.0 = 38.2 〜 70.2 点
  の間にデータの多く（2/3ぐらい）が集まっていることがわかる．
  　英語得点の標準偏差 11.6 点より，国語得点の標準偏差の方が大きいので，国語データ の方がデータがより拡がって分布していることがわかる．
  

4-4．形状の情報

• 単調減少（増加）型，単峰型，2峰型：ヒストグラムでわかる．
• 歪度（わいど）Skewness：歪度正→右に長く伸びる．歪度負→左に長く伸びる
• 尖度（せんど）Kurtosis：尖度 = 3 →正規分布と似た尖り． 尖度＞ 3 → 正規分布より尖る．尖度＜ 3 →正規分布よりなだらか．
  

データ分布（ヒストグラム）による標準偏差（SD）の違い

　以下のヒストグラムは，平均値は同じだが標準偏差が異なっている．
標準偏差（SD）が小さいときは分布が平均のまわりに集中し，大きいときは分布が広がり， データのちらばりが大きくなっている．

単峰（つり鐘型）	単峰（つり鐘型）	単峰型
単調減少型 メディアン（中央値）= 17.7，歪度＝1.1	U字型	2峰型
単峰型（左に裾が伸びる） 歪度＝-0.43	単峰型（右に裾が伸びる） 歪度＝0.45	単峰型（右に裾が伸びる） 歪度＝0.80