2009.5.21
携帯解答サイト： http://lbm.ab.a.u-tokyo.ac.jp/~omori/k/
中央値，四分位範囲の計算追加説明
　国語得点データで，25％点と75％点を求める方法で，学生からの指摘があった． とてもわかりやすいので，それを紹介する．ご指摘ありがとうございました． 75％点は，メディアンからのデータの順位33番から順位65番のメディアンで， 順位 33 + 16 = 49 番目（上から17番目）の66点．

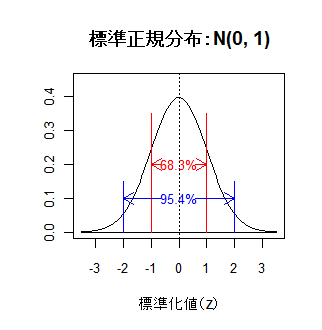
5-3．標準正規分布 N(0, 1)（続き）

標準正規分布 N(0, 1) では，-1 ≦ z ≦ 1 の範囲に全体の68.3％が含まれ， -2 ≦ z ≦ 2 の範囲に全体の95.4％が含まれる（下左図）．
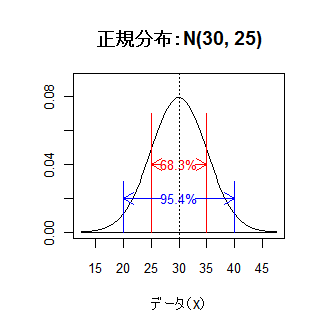
　また，平均 μ - 30， 分散 25 の正規分布 N(30, 25) では，標準偏差が σ = √25 = 5 なので， 25 ≦ x ≦ 35 の範囲に全体の68.3％が含まれ， 20 ≦ x ≦ 40 の範囲に全体の95.4％が含まれる（下右図）．
normal1 normal2
範囲に含まれる確率
　　N(0, 1)　　 　　N(30, 25)　　 　　N(μ，σ2)　　 　確率(％)
　-1 → 1 　25 → 35 　μ - σ → μ + σ 68.3
　-1.96 → 1.96 　20.2 → 39.8 　μ - 1.96σ → μ + 1.96σ 95.0
　-2 → 2 　20 → 40 　μ - 2σ → μ + 2σ 95.4
　-2.58 → 2.58 　17.1 → 42.9 　μ - 2.58σ → μ + 2.58σ 99.0
　-3 → 3 　15 → 45 　μ - 3σ → μ + 3σ 99.7

例題
標準正規分布では，-2から2までの間に全データのかなりの部分（95.4%）が含まれる． 平均 8，分散 4 の正規分布でこの区間に対応するのは何か．
平均μ＝8，標準偏差σ＝√4＝2．
小さい値＝μ−2σ＝8−2*2＝4， 大きい値＝μ＋2σ＝8＋2*2＝12． これより，4 〜 12，に全データのかなりの部分が含まれる．

5-4．正規分布のあてはめと Q - Q プロット

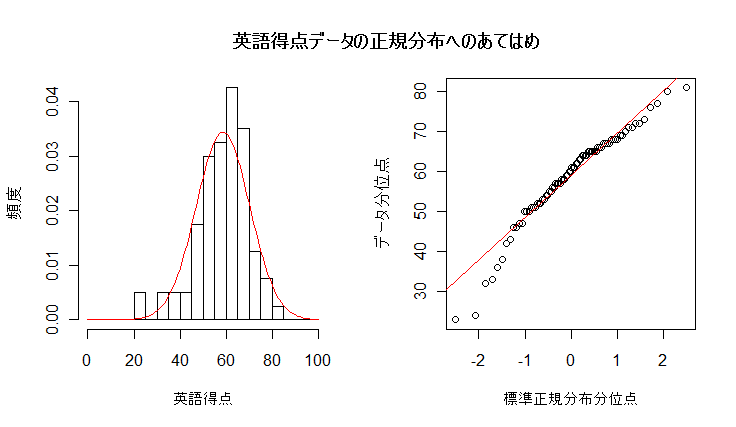
　以前，取り上げた英語得点データに正規分布をあてはめてみる．英語得点データの代表値は，
平均：58.6点，標準偏差：11.6点（分散：134.4）
であったので，平均 μ = 58.6，分散 σ2 = 134.4 の正規分布，
N(58.6, 134.4)
にあてはめればよい．

　データが正規分布によくあてはまっているかを視覚的にみる方法として，Q - Q プロットがある．
　これは，標準正規分布とデータの分位点との関係を図示したもので，これが，直線上に 乗っているとデータが正規分布によくあてはまっていることがわかる．
　このプロットを手でつくるのは難しいので，ソフトウエアで書かせる．ここでは，Q - Q プロット で正規分布へのあてはまりのよさがわかることを覚えておけば十分である．

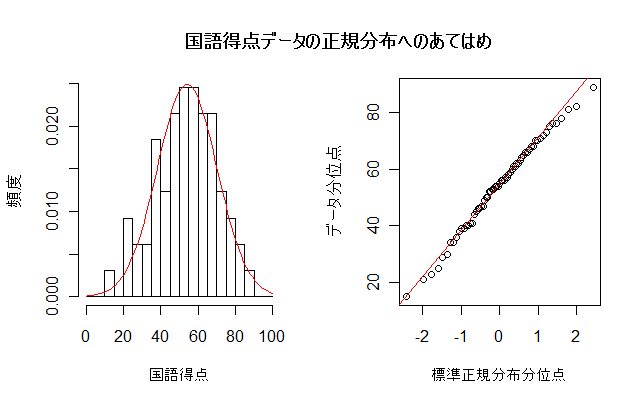
　国語得点データに正規分布をあてはめると，
平均：54.2点，標準偏差：16.0点（分散：255.3）
であったので，平均 μ = 54.2，分散 σ2 = 255.3 の正規分布，
N(54.2, 255.3)
にあてはめる．
問：英語と国語，どちらの方が正規分布へのあてはまりがよい と言えるか．選択肢解答テスト第２問で送信せよ．
　１．国語の方がよい　　 　２．英語の方がよい　　 　３．国語と英語は同じ　
Copyright (C) 2008, Hiroshi Omori. 最終更新：2008年 5月22日