2009.6.04
5-6. 正規分布に基づく母数の区間推定
分散既知の場合の母平均 μ の区間推定
正規分布する母集団で分散がわかっている場合は,未知の平均に関する区間推定ができる.
いま,正規分布 N( μ,σ2 ) において,大きさ n の標本を
抽出したとき,標本平均 x- は,
x- 〜 N( μ,σ2/n ) →
z = √n(x- − μ )/σ 〜 N(0, 1)
と分布する.標準正規分布の 97.5%分位点は 1.96 であるので,
標準正規分布する確率変数 z が -1.96 から 1.96 に入る確率は 0.95 となる.つまり,
Pr[ − 1.96 < z < 1.96 ] = 0.95,
Pr[ − 1.96 < √n(x-
− μ )/σ < 1.96 ] = 0.95,
Pr[ - 1.96×σ/ √n < x- − μ < 1.96×σ/ √n ] = 0.95,
Pr[ - 1.96×σ/ √n < μ − x-< 1.96×σ/ √n ] = 0.95,
Pr[ x- − 1.96×σ/ √n < μ
< x- + 1.96×σ/ √n ] = 0.95,
となる.最後の式を母集団平均 μ の 95% 信頼区間と言う.
このように,母数の信頼区間を標本から推定することを区間推定という.
- 例題
-
過去の経験から分散が 9 であることがわかっている正規母集団から大きさ 16 の標本を抽出
したところ,標本平均が 1.5 であった.標準正規分布の 97.5% 分位点を 1.96
として,母平均 μ の 95% 信頼区間を求めよ.
- 解答例
-
σ=√9=3,√n=√16=4,より,1.96×σ/ √n=1.96×3/4=1.47
よって,1.5 ± 1.47,つまり, 0.03 < μ < 2.97 が母平均 μ の 95% 信頼区間
となる.
95% の意味
同じ正規母集団から標本抽出を繰り返すと,毎回標本平均として異なる値がえられ,それに
対応して信頼区間も異なる.この信頼区間の 95% が真の平均 μ を含む,という意味である.
つまり,100回の標本抽出により,100 個の信頼区間を作ったら平均的にみて,95 個の信頼区間が
真の平均 μ を含むことが期待できる.
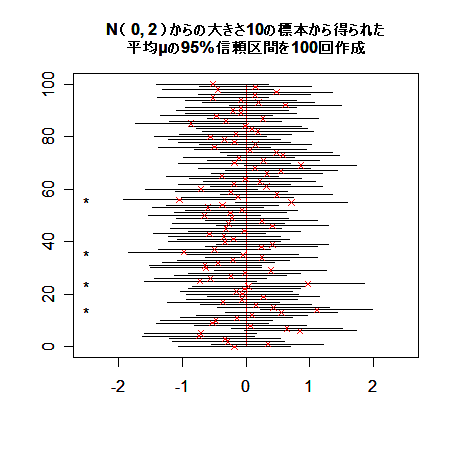
下の図は,平均 0 分散 2 の正規分布 N( 0, 2 ) から大きさ 10 の標本を取りだし,分散が既知であるとして,
母平均に対する信頼区間を 100 個生成したものである."×" が標本平均を示す.左の "*" は,信頼区間
が母平均の真値 0 を含まなかった場合である.
休講中の宿題
以下の問題に携帯もしくはパソコンから解答せよ.
携帯(パソコン)解答サイト: http://lbm.ab.a.u-tokyo.ac.jp/~omori/k/
数値解答テスト3で送信(半角数字) すること.
1問2点で,5問総得点が成績に加算される.何回間違えても
正解すれば得点できる.
- 問題
-
1000人が受験した英語試験がある.学生全体(母集団)の(母)平均は μ = 54点,(母)標準偏差は σ = 12点
であった.
以下の問に
標準正規分布累積確率表を見て答えよ.ただし,確率表を用いるときは,計算した値に最も
近い値に対する確率を使え.
第21問:上位100番以内に入るには,何点(整数)が必要か.
A 先生のクラスは 25 名であった.クラスは学生からランダム抽出(サンプリング)したものと仮定した.
第22問:クラスの平均得点の標準偏差(標準誤差)はいくらか(小数点第1位).
第23問:クラスの平均が50点以下である確率は何%(小数点第1位)か.
B 先生のクラスも 25 名であった.クラスの学生はランダムに選ばれ,A,B 先生で教え方
に差がないと仮定したとする.
第24問:A 先生のクラス平均と B 先生のクラス平均の差の標準偏差(標準誤差)はいくらか(小数点第1位).
第25問:A 先生のクラス平均が B 先生のクラス平均より 5 点高くなる確率は何%(整数)か.
Copyright (C) 2008, Hiroshi Omori. 最終更新:2009年 6月03日