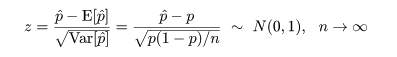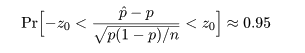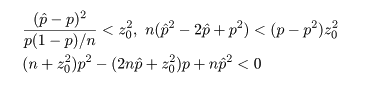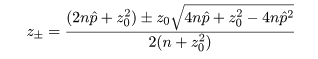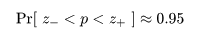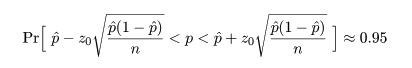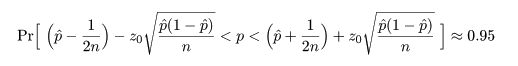2009.7.16

実験レポート

以下の実験は、来週木曜日（７月23日）から始めてください．締め切りは８月５日です。
　景観に対する知覚や感性の統計学的実験レポートを行ってください。 以下のサイトに行き、指示通りに実験を行って下さい。
注）実験終了者は前期得点が 5 点アップします。
http://lbm.ab.a.u-tokyo.ac.jp/~takami/kokusai.html

夏休みの宿題

集合知による景観解析

　多くの人の予想や意見を総合すると，よい予想や結果が得られることがある．これを， 集合知（collective inteligence）あるいは， 群衆の英知（wisdom of crowds）と呼んでいる．情報技術の進展により，多くの人の 意見を収集して集約することが比較的容易に行われるようになってきたので， 最近注目されている概念である．
　現在，多くの学生が写真機能つき携帯や，デジカメを所有している．また，ネット環境も充実しているので， 画像データを収集するのはとても容易になってきた．そこで，多くの学生に画像データを収集してもらい， ターゲットとなる東京国際大学の屋外景観の特徴付けを行うことを試みる．

課題

　東京国際大学の第１キャンパスと第２キャンパスの屋外景観で気に入った１つの景観を 携帯等でなるべく大きな画素数で撮影し，撮影場所，この景観を選んだ理由をなるべくたくさん記載して，
omori@lbm.ab.a.u-tokyo.ac.jp
まで写メールで送れ．メールには題名等で国際大の課題提出であることが一目でわかるようにすること．
注）課題提出者は後期成績が 5 点アップする．

７．比率に関する検定

　製品の不良率，政権への支持率，テレビ視聴率などの比率に関する統計的推論を取り扱う． 比率に関して基礎となる二項分布を学び，それを正規分布に近似して統計的推論を行うことを学ぶ．

7-1．二項分布

　成功確率 p の事象を n 回試行したときの成功回数 r の分布
r 〜 B(n, p) と書く．
　成功回数が r となる確率 Pr[r ] は，n 回の試行で r 回成功する 場合の数が nCr 通りで，r 回成功し n−r 回失敗するので，

Pr[r ] ＝ nCr pr (1−p)n−r

となる．

例題

A 選手は 3 割バッターである．ある試合で 5 回打席に立ったときときのヒット数の分布を求める．
この場合，p＝0.3，n＝5である．

　これより，ヒット数の分布は以下の表のように書ける．

  ヒット数      0       1       2       3       4       5   
確　率       0.16807          0.36015          0.3087          0.1323       0.02835       0.00243   

一般に，二項分布などの離散確率分布は，取ることができる値 xi ごとに，その値をとる 確率 pi，Σ pi ＝ 1， が定義されている．つまり，

値   x1     x2     …     xn  
  確　率     p1   p2   …   pn

の形で表現される．このとき，確率分布の平均と分散は，
平均： x- = x1p1 + x2p2 + … + xnpn = Σixipi
分散: s2 = (x1 - x-)2p1 + (x1 - x-)2p1 + … + (xn - x-)2pn = Σi(xi - x-)2pi
と定義される．

　これより，ヒット数の平均と分散は，

平均： x- = 0*0.16807 ＋ 1*0.36015 ＋ 2*0.3087 ＋ 3*0.1323 ＋ 4*0.02805 ＋ 5*0.00243 = 1.5
分散： s2 = (0−1.5)2*0.16807＋(1−1.5)2*0.36015 ＋(2−1.5)2*0.3087
＋ (3−1.5)2*0.1323＋(4−1.5)2*0.02805 ＋(5−1.5)2*0.00243 = 1.05

と計算される．実は，成功確率 p の事象を n 回行ったときの二項分布 B(n，p) の平均と分散は，
平均： x- = np = 5*0.3 = 1.5， 分散： s2 = np(1 - p) = 5*0.3*0.7 = 1.05
となることがわかる．

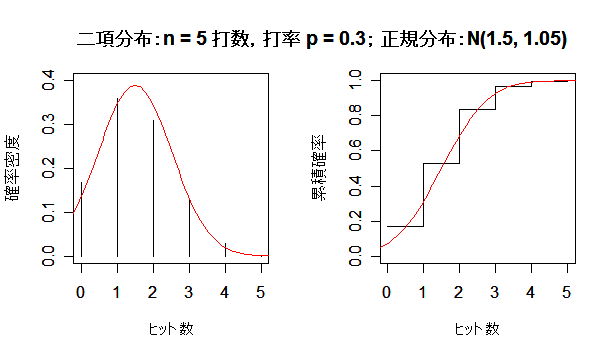
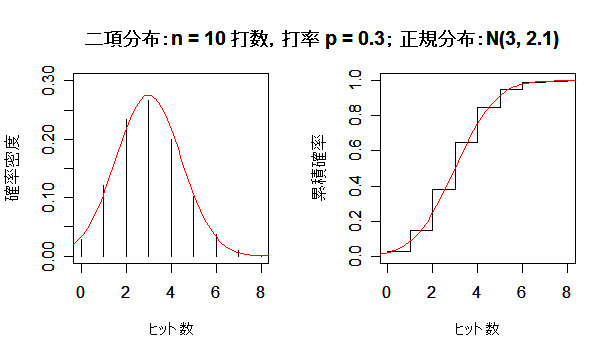
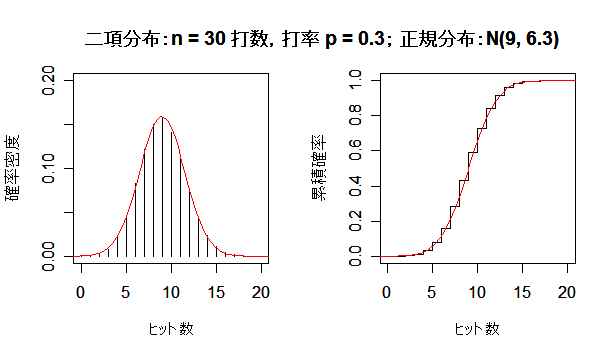
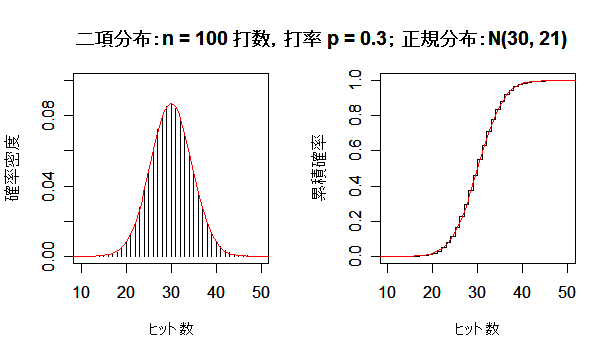
二項分布が正規分布に近づく様子

　成功確率 p の二項分布は，試行回数 n を増やしていくと，平均 np，分散 np(1 - p) の正規分布 に近づく．左図が確率分布（密度）で，右図が累積分布である．
binormal
binormal
binormal
binormal

7-2．成功確率（比率）の信頼区間

　成功確率 p のベルヌイ試行を n 回行ったとき x 回成功したとすると，成功確率は， p^ = x/n，と推定される．
　成功回数 x は二項分布し，その平均は E[x ] = np，分散は Var[x ] = np(1 - p)，で あるので，成功確率推定量 p^ の平均は E[p^ ] = E[x/n] = p， 分散は Var[p^ ] = Var[x/n] = Var[x ]/n2 = p(1 - p)/n， となる．これより，
binotest
と漸近的に分布するので，標準正規分布の 97.5％点の z0 = 1.96 を用いると， 近似的に
binotest
という不等式が成り立つ．これを整理すると，
binotest
という p の２次不等式を解くことに帰着する．いま，p の２次方程式の根を
binotest
とすると，この根を用い，p の 95％信頼区間は近似的に
binotest
となる．

　試行回数 n が十分大きいと思われるときは，さらに近似を加え， 成功確率推定量 p^ の分散において，真の成功確率 p の 代わりにその推定量 p^ に置き換えて，Var[p^ ] = p^(1 - p^)/n，とみなすと， p の 近似的な 95％信頼区間は，

binotest
と簡略化される．
　簡略化された信頼区間で連続性の補正を入れるには，
binotest
として，信頼区間の幅を拡げる．

　ところで，正規近似による信頼区間の構成では，場合により信頼区間が負になったり 1 を超えることがあるが， このときは，0 と 1 で切り詰める．

例題（テレビ視聴率）
テレビ視聴率は，視聴率の高い番組ほど多くの視聴者が見ているので，広告宣伝の効果が高く影響力が 強いと考えられている．このため，視聴率の高さが広告宣伝費用に反映されるので，テレビ会社は高い視聴率を 得ようとして番組を製作している．
ある調査会社のデータによると，関東地区では 600 世帯を対象にしているようである． NHK 大河ドラマの関東地区世帯視聴率は26.2％であった． 真の世帯視聴率の 95 ％信頼区間を求めよ．
解答：
p の分散推定値は s2 = p^(1 - p^)/n = 0.262*(1 - 0.262)/600 = 0.262*0.738/600 = 0.00032226
p の標準偏差の推定値（標準誤差）は s = √0.00032226 = 0.01795
95 ％信頼区間の幅は d = z0s = 1.96*0.01795 = 0.035
下限は，p^ - d = 0.262 - 0.035 = 0.227， 上限は，p^ + d = 0.262 + 0.035 = 0.297
よって，0.227 < p < 0.297 である．
Copyright (C) 2008, Hiroshi Omori. 最終更新：2009年 7月16日