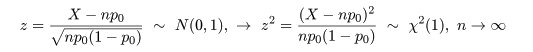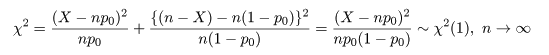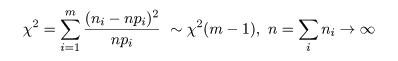2009.9.24
東京国際大学
統計学の基礎(後期)
東京大学大学院農学生命科学研究科 大森宏
前期試験の解説
標準正規分布累積確率表
問題1
あるクラスの漢字テスト成績の一部は,
53,62,58,60,68,54,65,70,63,57
であった.このデータの標本平均と標本標準偏差を小数点第2位まで求めよ.
- 解答例
-
データ数:n = 10
標本平均:x- = (53 + 62 + 58 + 60 + 68 + 54 + 65 + 70 + 63 +57)/10 = 610/10
= 61.00
上の計算表より,
標本分散:s2 = 290/9 = 32.22.標本標準偏差:s = √32.22 = 5.68
問題2
学生数 800 名の X 大学で英語テストを行った.その平均は 55 点,標準偏差 8 点であった.
A 君の得点は 62 点であった.
得点分布が正規分布に従っているとすると,A 君の順位は何番位か,また,上位 50 番以内になるには何点が必要か.
- 解答例
-
A 君の標準化得点: z = (x - μ)/σ = (62 - 55)/8 = 0.875
表から z > 0.875 となる確率: Pr[ z > 0.875 ] ≒ Pr[ z > 0.88 ] = 1 - Pr[ z < 0.88 ] =
1 - 0.811 = 0.189
A 君より成績がよいのは学生の 0.189(18.9%): 800 × 0.189 = 151.2 → 150 番位
-
上位 50 番 → 上位 50/800 = 0.0625(6.25%)→ 1 - 0.0625 = 0.9375 ≒ 0.938 = Pr[ z < 1.54 ]
→ x = μ + zσ = 55 + 1.54×8 = 67.32 → 68 点以上必要
問題3
上の大学で,B先生は2つのクラスを受け持っていた.1 組の 20 名は工学部,2 組の 40 名は文学部学生であった.
1 組の平均点は 53.2 点,2 組の平均点は 57.4 点であった.学生個人の英語得点分布は正規分布に従い,
標準偏差は 8 点であるとしてよい.
問1 1 組の平均点と 2 組の平均点の標準偏差(標準誤差)をそれぞれ求めよ.
- 解答例
-
学生個人得点 xi が平均 μ,分散 σ2 の正規分布に従う,
xi 〜 N( μ, σ2 ),とすると,n 人の平均 x- は,
平均 μ,分散 σ2/n の正規分布に従う,x- 〜 N( μ, σ2/n ),
である.これより,平均 x- の標準偏差(標準誤差)は σ/√n となる.
1組:n = 20 → 標準誤差:σ/√n = 8/√20 = 1.79
2組:m = 40 → 標準誤差:σ/√m = 8/√40 = 1.26
問2 1 組は工学部学生からランダムに取られたものと仮定したときの
工学部学生全体での英語平均得点の 95 %信頼区間
- 解答例
-
工学部学生全体の英語得点平均を μt とする.標準偏差は題意より σ = 8 とみなせる.
そこからランダムにサンプリングした n = 20 名の平均得点が x- = 53.2 であった.
平均得点 x- の標準偏差(標準誤差)は問1より,
σ/√n = 8/√20 = 1.79 である.
これより母平均 μ の信頼区間は,
x- - 1.96 × σ/√n < μt < x- + 1.96 × σ/√n
53.2 - 1.96 × 1.79 < μt < 53.2 + 1.96 × 1.79
53.2 - 3.5 < μt < 53.2 + 3.5
49.7 < μt < 56.7
である.
問3 1 組の平均と 2 組の平均の差の標準偏差(標準誤差)
- 解答例
-
1 組の平均得点を x-,2 組の平均得点を y- とする.また,
工学部学生の英語得点の母平均を μt,文学部学生の母平均を μl とする.
問1,問2より,
x- 〜 N( μt, σ2/n ),
y- 〜 N( μl, σ2/m ),
となる.すると,1 組の平均と 2 組の平均の差 x- - y- は,
x- - y- 〜 N( μt - μl,
σ2/n + σ2/m)
と分布する.すなわち,x- - y- の分散は,
σ*2 = σ2/n + σ2/m = σ2(1/n + 1/m) =
82(1/20 + 1/40) = 82×3/40
である.これより,x- - y- の標準偏差(標準誤差)は,
σ* = √(82×3/40) = 8√(3/40) = 2.19
問4 工学部学生(1 組)と文学部学生(2 組)で英語の実力に違いがあるか検定せよ.
- 解答例
-
帰無仮説として,工学部学生と文学部学生で英語の実力に違いがないとする.
これより,
H0:μt = μl → μt - μl = 0
となる.帰無仮説のもとで,
1 組の平均と 2 組の平均得点の差 x- - y- は,
x- - y- 〜 N( 0,
σ2/n + σ2/m) = N( 0, σ*2 )
と分布するので,
これを標準化した z は,
z = (x- - y-)/σ*
〜 N(0,1)
と標準正規分布に従う.標準正規分布表から検定ができる.
検定統計量 |z| は,
|z| = |x- - y-|/σ*
= | 53.2 - 57.4 |/2.19 = 4.2/2.19
= 1.92
1.92 は標準正規分布の 97.5%点(有意水準両側 5%)の 1.96 よりは小さいので,5 %有意でない.
よって,工学部学生と文学部学生では英語の実力に違いがあるとは認められなかった.
- 解答例2
-
問3より,1 組の平均と 2 組の平均の差 x- - y- は,
x- - y- 〜 N( μt - μl,
σ2/n + σ2/m) = N( μt - μl, σ*2 )
と分布する.これより,工学部学生と文学部学生の英語得点平均の差 μt - μl の 95 %
信頼区間は,
( x- - x- ) - 1.96 × σ* < μt - μl
< ( x- - x- ) + 1.96 × σ*
(53.2 - 57.4) - 1.96 × 2.19 < μt - μl < (53.2 - 57.4) + 1.96 × 2.19
-4.2 - 4.3 < μt - μl < -4.2 + 4.3
-8.5 < μt - μl < 0.1
となる.95 %信頼区間が 0 を含むので,帰無仮説
H0:μt - μl = 0
は棄却されない.すなわち,工学部学生と文学部学生の英語得点平均に有意な差があるとは認められなかった.
問題4
以下の事項を簡単に説明せよ
問1 標本抽出
-
母集団の特徴を調べるときに,コストなどの面で全数調査が難しいときがある.このような場合,母集団の
一部の成員を選び,選ばれた個体の特徴を調べる.これを標本抽出(サンプリング)という.このとき,
選ばれた個体に偏りが出ないように,無作為抽出(ランダムサンプリング)を行うことが重要である.
問2 第1種の過誤
-
標本に対して統計的検定を行い判断を下したとき,2種類の過誤(間違い)がある.
このうち,帰無仮説が真の(正しい)とき誤って帰無仮説を棄却することを第1種の過誤(タイプ1エラー)
という.一方,帰無仮説が偽の(間違っている)とき誤って帰無仮説を受諾することを第2種の過誤
(タイプ2エラー)という.
なお,統計的検定において,第1種の過誤の確率を有意水準といい,これを制御して検定方式を組み立てている.
有意水準には,通常,5%や 1%がよく用いられる.
.
8.適合度検定
8-1.χ2 分布(カイ2乗分布)
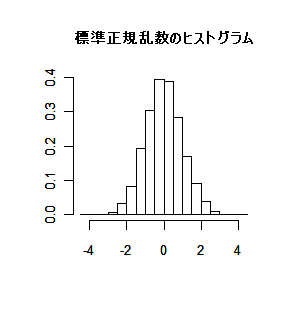
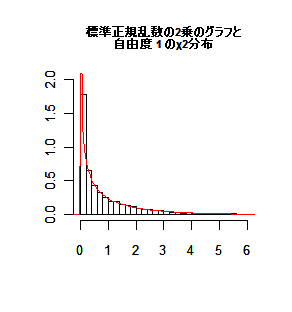
標準正規分布する確率変数の 2 乗は自由度(df: degree of freedom)
1 の χ2 分布
( χ2 (1) )に従う.
zi 〜 N(0, 1) →
zi2 〜
χ2 (1)
zi :
-1.2051165, -1.3398190, 1.5698995, -0.1302181, -0.7212650,…
zi2 :
1.45230569, 1.79511499, 2.46458454, 0.01695676, 0.52022319,…
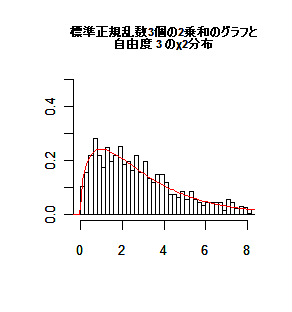
互いに独立に標準正規分布する確率変数の 2 乗の n 個の和は,
自由度 n の χ2 分布
( χ2 (n))に従う.
[(標準正規分布データ)2 の n 個の和] 〜
χ2 (n)
→
Xn = z12+ … +
zn2 〜
χ2 (n)
標準正規乱数 3 個の 2 乗和,X3 :
2.752467, 1.167955, 4.857822, 4.013744, 1.727430,…
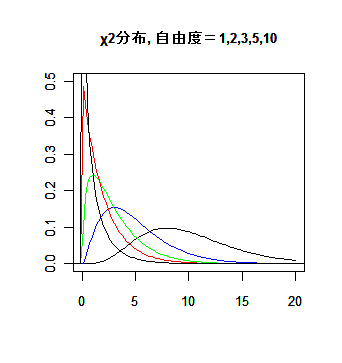
χ2 分布を用いた検定では,χ2 分布の 95 %点(有意水準 5 %)と 99 %点
(有意水準 1 %)の表を参照すればよい.ここでは,参考のため 90 %点(やや有意)も与えておく.
χ2 分布の%点
| 自由度 | 90% |
95% | 99% |
|---|
| 1 | 2.71 | 3.84 | 6.64 |
|---|
| 2 | 4.61 | 5.99 | 9.21 |
|---|
| 3 | 6.25 | 7.81 | 11.34 |
|---|
| 4 | 7.78 | 9.49 | 13.28 |
|---|
| 5 | 9.24 | 11.07 | 15.09 |
|---|
| 6 | 10.64 | 12.59 | 16.81 |
|---|
8-2.ピアソンの χ2 適合度検定
前期最後に行った比率の検定は,χ2 分布を用いる適合度検定と大きな関係がある.
ここでは n 回のベルヌイ試行(成功か失敗のどちらかが得られる試行)
で X 回成功したときに,成功確率が p0 であるという,
帰無仮説,H0: p = p0,
対立仮説,H1: p ≠ p0,
の検定を考えた.そこでは,X を標準化して標準正規分布にもって行ったが,これを2乗して
χ2 分布を用いることもできる.すなわち,
という関係がある.
ところで,n 回のベルヌイ試行の結果と帰無仮説のもとでの期待値を表にすると,
| | 成 功 | 失 敗 |
|---|
| 観測度数 | X | n - X |
|---|
| 期待度数 | np0 | n(1 - p0) |
|---|
となる.ここで,ピアソン(Pearson)のχ2 値,
を計算すると,
となる.つまり,χ2 値は,試行回数 n が大きくなるにつれて
帰無仮説のもとで自由度 1 の χ2 分布に漸近的に従う.よって,これより検定が行える.
8-3.確率分布との適合度
データが想定している確率分布に適合しているかは,ピアソン(Peason)の χ2 適合度検定で行う
ことができる.いま,離散分布の,たとえば m = 5 のセルに対して,観測されたカウントデータと対応する
想定確率が,
| | セル1 | セル2 | セル3 |
セル4 | セル5 | 計 |
|---|
| 観測度数 | n1 | n2 |
n3 | n4 |
n5 | n |
|---|
| 想定確率分布 | p1 | p2 |
p3 | p4 |
p5 | 1 |
|---|
のようになっていたとする.このとき,ピアソン(Peason)の χ2 値は,
のように近似的に自由度 m - 1 の χ2 分布に従う.これにより,データが想定確率分布に
適合しているかの検定が行える.検定の帰無仮説は,
H0:データは想定確率分布に従う.
である.
- 例題
-
A 君と B 君が将棋を行った.10 局やったところ,A 君の 7 勝 3 敗であった.A 君と B 君で将棋の強さに
違いがあるか検定せよ.また,30 局やって,A 君の 21 勝 9 敗であったとき(勝率は 7 割で先ほどと同じ)
ではどうか.
- 解答
-
帰無仮説として,A 君と B 君の将棋の強さが等しい,とする.すなわち,A 君の勝率が 0.5 であるとする.
よって,
H0: p = 0.5
である.
帰無仮説のもとで,A 君の勝ち負けの期待度数は,5 勝 5 敗であるので,
| | 勝 ち | 負 け |
|---|
| 観測度数 | 7 | 3 |
|---|
| 期待度数 | 5 | 5 |
|---|
のような表ができる.これより,
χ2 = (7 - 5)2/5 + (3 - 5)2/5 = 4/5 + 4/5 = 8/5 = 1.6
となる.1.6 < 3.84 なので,帰無仮説は棄却されない.つまり,A 君と B 君の将棋の強さは同じと考えても
よい.
なお,前節の正規分布を用いた検定では,検定統計量が z = 1.265 であったが,
適合度検定では,χ2 = 1.2652 = 1.6 となっていることに注意せよ.
A 君が 21 勝 9 敗であったときは,期待度数は 15 勝 15 敗である.計算をしやすいように表の
行と列を入れ替えてみる.
| | 観測度数 | 期待度数 |
偏差の計算 | χ2 値 |
|---|
| 勝 ち | 21 | 15 |
(21 - 15)2/15 | 12/5 |
|---|
| 負 け | 9 | 15 |
(9 - 15)2/15 | 12/5 |
|---|
| 計 | 30 | 30 |
| 24/5 = 4.8 |
|---|
となる.3.84 < 4.8 < 6.64 なので,帰無仮説は有意水準 5 %で(1 %ではない)棄却される.
つまり,A 君と B 君の将棋の強さは同じとは考えられず,A 君の方が強いと言える.
- 問題
-
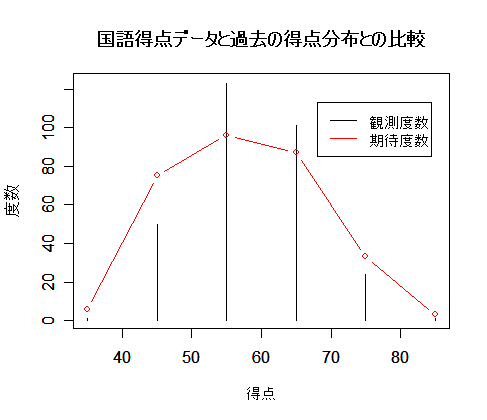
ある大学で国語の試験を行ったところ以下のような得点分布を得た.過去の得点分布と同じ
であるかを表のマス目を埋めることにより,検定せよ.
Copyright (C) 2008, Hiroshi Omori. 最終更新:2009年 9月24日