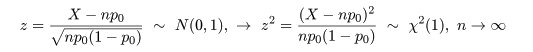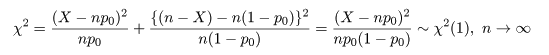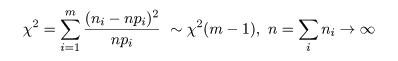2010.10.04
8.適合度検定
8-1.χ2 分布(カイ2乗分布)
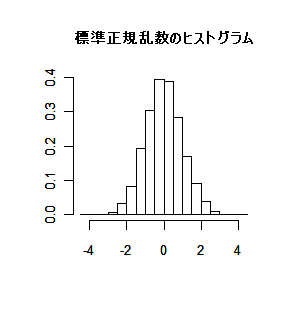
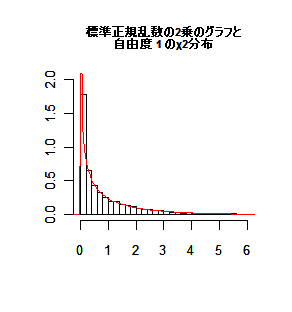
標準正規分布する確率変数の 2 乗は自由度(df: degree of freedom)
1 の χ2 分布
( χ2 (1) )に従う.
zi 〜 N(0, 1) →
zi2 〜
χ2 (1)
zi :
-1.2051165, -1.3398190, 1.5698995, -0.1302181, -0.7212650,…
zi2 :
1.45230569, 1.79511499, 2.46458454, 0.01695676, 0.52022319,…
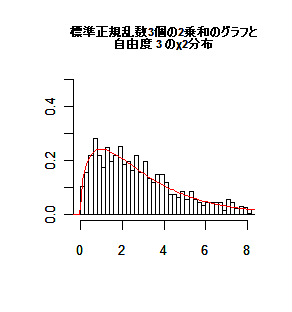
互いに独立に標準正規分布する確率変数の 2 乗の n 個の和は,
自由度 n の χ2 分布
( χ2 (n))に従う.
[(標準正規分布データ)2 の n 個の和] 〜
χ2 (n)
→
Xn = z12+ … +
zn2 〜
χ2 (n)
標準正規乱数 3 個の 2 乗和,X3 :
2.752467, 1.167955, 4.857822, 4.013744, 1.727430,…
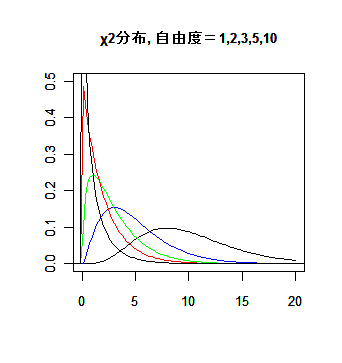
χ2 分布を用いた検定では,χ2 分布の 95 %点(有意水準 5 %)と 99 %点
(有意水準 1 %)の表を参照すればよい.ここでは,参考のため 90 %点(やや有意)も与えておく.
χ2 分布の%点
| 自由度 | 90% |
95% | 99% |
|---|
| 1 | 2.71 | 3.84 | 6.64 |
|---|
| 2 | 4.61 | 5.99 | 9.21 |
|---|
| 3 | 6.25 | 7.81 | 11.34 |
|---|
| 4 | 7.78 | 9.49 | 13.28 |
|---|
| 5 | 9.24 | 11.07 | 15.09 |
|---|
| 6 | 10.64 | 12.59 | 16.81 |
|---|
8-2.ピアソンの χ2 適合度検定
前期最後に行った比率の検定は,χ2 分布を用いる適合度検定と大きな関係がある.
ここでは n 回のベルヌイ試行(成功か失敗のどちらかが得られる試行)
で X 回成功したときに,成功確率が p0 であるという,
帰無仮説,H0: p = p0,
対立仮説,H1: p ≠ p0,
の検定を考えた.そこでは,X を標準化して標準正規分布にもって行ったが,これを2乗して
χ2 分布を用いることもできる.すなわち,
という関係がある.
ところで,n 回のベルヌイ試行の結果と帰無仮説のもとでの期待値を表にすると,
| | 成 功 | 失 敗 |
|---|
| 観測度数 | X | n - X |
|---|
| 期待度数 | np0 | n(1 - p0) |
|---|
となる.ここで,ピアソン(Pearson)のχ2 値,
を計算すると,
となる.つまり,χ2 値は,試行回数 n が大きくなるにつれて
帰無仮説のもとで自由度 1 の χ2 分布に漸近的に従う.よって,これより検定が行える.
8-3.確率分布との適合度
データが想定している確率分布に適合しているかは,ピアソン(Peason)の χ2 適合度検定で行う
ことができる.いま,離散分布の,たとえば m = 5 のセルに対して,観測されたカウントデータと対応する
想定確率が,
| | セル1 | セル2 | セル3 |
セル4 | セル5 | 計 |
|---|
| 観測度数 | n1 | n2 |
n3 | n4 |
n5 | n |
|---|
| 想定確率分布 | p1 | p2 |
p3 | p4 |
p5 | 1 |
|---|
のようになっていたとする.このとき,ピアソン(Peason)の χ2 値は,
のように近似的に自由度 m - 1 の χ2 分布に従う.これにより,データが想定確率分布に
適合しているかの検定が行える.検定の帰無仮説は,
H0:データは想定確率分布に従う.
である.
- 例題
-
A 君と B 君が将棋を行った.10 局やったところ,A 君の 7 勝 3 敗であった.A 君と B 君で将棋の強さに
違いがあるか検定せよ.また,30 局やって,A 君の 21 勝 9 敗であったとき(勝率は 7 割で先ほどと同じ)
ではどうか.
- 解答
-
帰無仮説として,A 君と B 君の将棋の強さが等しい,とする.すなわち,A 君の勝率が 0.5 であるとする.
よって,
H0: p = 0.5
である.
帰無仮説のもとで,A 君の勝ち負けの期待度数は,5 勝 5 敗であるので,
| | 勝 ち | 負 け |
|---|
| 観測度数 | 7 | 3 |
|---|
| 期待度数 | 5 | 5 |
|---|
のような表ができる.これより,
χ2 = (7 - 5)2/5 + (3 - 5)2/5 = 4/5 + 4/5 = 8/5 = 1.6
となる.1.6 < 3.84 なので,帰無仮説は棄却されない.つまり,A 君と B 君の将棋の強さは同じと考えても
よい.
なお,前節の正規分布を用いた検定では,検定統計量が z = 1.265 であったが,
適合度検定では,χ2 = 1.2652 = 1.6 となっていることに注意せよ.
A 君が 21 勝 9 敗であったときは,期待度数は 15 勝 15 敗である.計算をしやすいように表の
行と列を入れ替えてみる.
| | 観測度数 | 期待度数 |
偏差の計算 | χ2 値 |
|---|
| 勝 ち | 21 | 15 |
(21 - 15)2/15 | 12/5 |
|---|
| 負 け | 9 | 15 |
(9 - 15)2/15 | 12/5 |
|---|
| 計 | 30 | 30 |
| 24/5 = 4.8 |
|---|
となる.3.84 < 4.8 < 6.64 なので,帰無仮説は有意水準 5 %で(1 %ではない)棄却される.
つまり,A 君と B 君の将棋の強さは同じとは考えられず,A 君の方が強いと言える.
- 問題
-
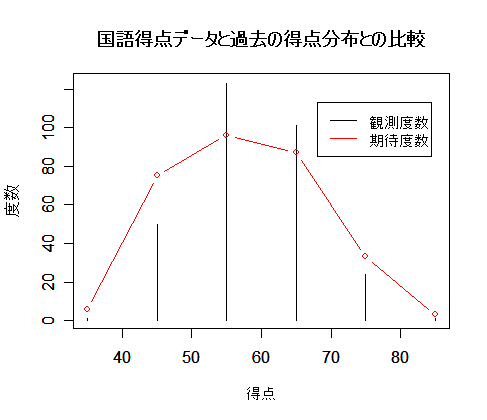
ある大学で国語の試験を行ったところ以下のような得点分布を得た.過去の得点分布と同じ
であるかを表のマス目を埋めることにより,検定せよ.
国語得点の過去の分布との比較
| 得点 | 観測値 | 過去の分布 | 期待度数 |
偏差の計算 | χ2 値 |
| 80〜89 | 1 | 0.01 |
| | |
| 70〜79 | 24 | 0.11 |
| | |
| 60〜69 | 101 | 0.29 |
| | |
| 50〜59 | 123 | 0.32 |
| | |
| 40〜49 | 50 | 0.25 |
| | |
| 30〜39 | 1 | 0.02 |
| | |
| 計 | 300 | 1 |
| | |
Copyright (C) 2008, Hiroshi Omori. 最終更新:2010年10月04日