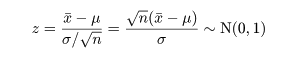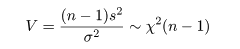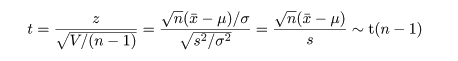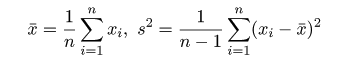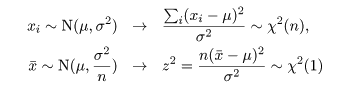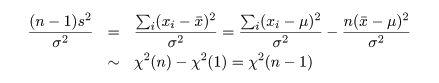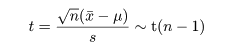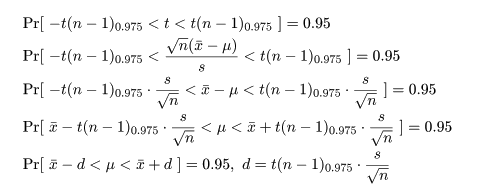2010.11.08

10．t 検定

10-1. t 分布

定義

　標準正規分布に従う確率変数を z，(z ～ N(0,1))，
自由度 n の χ2 分布に従う 確率変数を V，(V ～ χ2(n))， とする．
両者が独立であるとすると，その比 t は，自由度 n の t 分布，t(n)，に従う．

分散未知のときの標本平均の分布

　正規母集団 N( μ，σ2 ) から大きさ n の 標本を取り出したとき，標本平均 x- を標準化したもの z は，
と標準正規分布に従う．
　母標準偏差 σ が未知であるときこれを標本標準偏差 s で置き換えた ものを t 値といい，自由度 n － 1 の t 分布に従う．
これは，標本分散の分布から
であるので，比を取ると，
となるからである．

t 検定に用いる t 分布表

標本分散の分布

　正規母集団で，母数が未知であるときを考える． 大きさ n の標本 x1，x2，…，xn を抽出したとき，母平均 μ と母分散 σ2 は，そえぞれ 標本平均 x- と標本分散 s2，
sampmv
で推定される． 　標本や標本平均は，
sampmv
と分布する．一方，
sampmv
と計算されるので，(n - 1)s2/σ2 という量は，
sampmv
と，自由度 n - 1 の χ2 分布，χ2(n - 1)，に従うことがわかる．

　自由度 n - 1 の χ2 分布の平均は n - 1 なので， (n - 1)s2/σ2 の平均（期待値）は，

E[ (n - 1)s2/σ2 ] = (n - 1)/σ2 E[ s2 ] = n - 1

となる．これより，標本分散 s2 の期待値は，E[ s2 ] = σ2 となる． このように，母（集団）分散の推定量の期待値（平均）が母集団分散 に等しくなる．このような性質を不偏という．母分散 σ2 として，偏差平方和 ∑(xi - x-)2 を n で割らずに n - 1 で割るのは，推定値 が不偏になるためである．このことを強調して，s2 を不偏分散と呼ぶこともある．

10-2．分散未知のときの母平均 μ の区間推定

正規母集団 N( μ，σ2 ) から大きさ n の 標本を取り出したとき，標本平均が x- で標本分散が s2 であるとすると，t 値は
のように自由度 n - 1 の t 分布に従う．
　自由度 n - 1 の t 分布の 97.5％分位点を t(n - 1)0.975 とすると， t 分布する確率変数 t が -t(n - 1)0.975 から t(n - 1)0.975 に入る 確率は 0.95 となる．つまり，
tCI
となる．最後の式を母分散未知のときの母集団平均 μ の 95％ 信頼区間と言う．

例題
正規母集団から大きさ 16 の標本を抽出したところ，標本平均が 1.5 で，標本分散が 9 であった．母集団平均 μ の 95％ 信頼区間を求めよ．
解答
t0 s / √n ＝ 2.13×√9/√16 = 2.13×3/4 ＝ 1.60，
よって，1.5 ± 1.60，つまり， -0.1 ＜ μ ＜ 3.10 が母平均 μ の 95％ 信頼区間 となる．

注）母集団分散が σ2 ＝ 9 とわかっていたとき （6.14号）と少し違うことに注意せよ．
このときの母集団平均 μ の 95％ 信頼区間は，

Pr[ x- － 1.96×σ/ √n ＜ μ ＜ x- ＋ 1.96×σ/ √n　] ＝ 0.95，

である．このときの例題は，
例題
過去の経験から分散が 9 であることがわかっている正規母集団から大きさ 16 の標本を抽出 したところ，標本平均が 1.5 であった．標準正規分布の 97.5％ 分位点を 1.96 として，母平均 μ の 95％ 信頼区間を求めよ．
解答例
σ＝√9＝3，√n＝√16＝4，より，1.96×σ/ √n＝1.96×3/4＝1.47
よって，1.5 ± 1.47，つまり， 0.03 ＜ μ ＜ 2.97 が母平均 μ の 95％ 信頼区間 となる．

すなわち，分散が未知のとき（これが普通）は，分散の推定値である標本分散を用いるので， 推定誤差が伴う．この誤差を考慮した t 分布で信頼区間を構成するので，信頼区間が広くなり， 母平均の推定精度が悪くなる．

Copyright (C) 2008, Hiroshi Omori. 最終更新：2010年11月05日