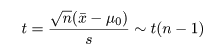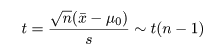2010.11.15

10-3. 母平均に対する t 検定

例題

通常の飼育方式では，鶏の１ヶ月の成長量が平均 100gであることが知られて いるとする．新方式 A による飼育方法を 25 羽で試したところ，平均成長量が 105g であり， 標本標準偏差が 10g であった．新方式 A は通常の飼育方式と成長量が有意に異なるか 検定せよ．ただし，自由度 24 の t 分布の 97.5％パーセント点は 2.06 であり， 99.5％点は 2.80 である．

解答例

新方式による成長量の母集団平均を μ とおき，通常の飼育方式の成長量の 母集団平均を μ₀ ＝ 100 とおく．
この問題での帰無仮説（H₀）と対立仮説（H₁）は，

H₀：μ ＝ μ₀
H₁：μ ≠ μ₀

と定式化される．検定に用いる検定統計量は，標本平均を標準化した t 値の絶対値 である．
標本の大きさ n ＝ 25 の標本の標本 平均 x^- ＝ 105より，

|t | ＝ √n | x^- − μ₀ |/s ＝5|105−100|/10＝2.5

である．新方式の標本平均の標準化値の絶対値 |t | ＝ 2.5 は，両側 5 ％点（片側 2.5 ％点） の 2.06 よりは 大きく，両側 1 ％点（片側 0.5 ％点）の 2.80 よりは小さい．
よって，新方式は通常方式と成長量は 5 ％水準で有意に異なると言えるが，1 ％水準 では有意でない．つまり，5 ％有意である．

10-4. 母平均に対する t 検定（信頼区間との関係）

• 母分散既知 −＞ | z | ＝ √n ×| x^- | /σ ＞ 1.96 なら帰無仮説を棄却．
• 母分散未知 −＞ | t | ＝ √n ×| x^- | /s ＞ t₀ なら帰無仮説を棄却．

例題

過去の経験から分散が 9 であることがわかっている正規母集団から大きさ 16 の標本を抽出 したところ，標本平均が 1.5 であった．母平均が 0 であるという帰無仮説 H₀：μ ＝ 0， を検定せよ．

解答

| z | ＝ √n ×| x^- | /σ = √16×1.5/3 = 2 ＞ 1.96，
となり，| z | 値が標準正規分布の 97.5％点の 1.96 より大きいので帰無仮説は有意水準 5％で 棄却される．

先ほどの例では， 0.03 ＜ μ ＜ 2.97 が母平均 μ の 95％ 信頼区間 であった．
母平均 μ の 95％信頼区間が 0 を含んでいないので帰無仮説 H₀：μ ＝ 0 は棄却される， と考えてもよい．

例題

正規母集団から大きさ 16 の標本を抽出 したところ，標本平均が 1.5 で標本分散が 9 であった． 母平均が 0 であるという帰無仮説 H₀：μ ＝ 0， を検定せよ．

解答

自由度 15 の t 分布の 97.5％点は t 分布表から 2.13 である．
| t | ＝ √n ×| x^- |s / = √16×1.5/3 = 2 ＜ 2.13
となり，| t | 値がこの 2.13 より小さいいので帰無仮説は棄却されない．

先ほどの例では， -0.1 ＜ μ ＜ 3.10 が母平均 μ の 95％ 信頼区間 であった．
母平均 μ の 95％信頼区間が 0 を含んでいるので帰無仮説 H₀：μ ＝ 0 は棄却されない， と考えてもよい．

例題

あるダイエット法 A を無作為に選ばれた 6 名が 3ヶ月間試したところ，以下のデータを得た．この方法に効果があるかを検定してみる．
　帰無仮説は，「ダイエット法 A に効果がない．」であり，ダイエット法の使用前から使用後での体重の減少が０より 有意に大きいか，を検定することで効果の判定が行える．すなわち，

ダイエットの効果：減少量平均 ＝ （使用前体重 − 使用後体重）の平均

としたとき，

帰無仮説　H₀ ： 減少量平均 ＝ 0

対立仮説　H₁ ： 減少量平均 ≠ 0

と定式化される． 以下の表の空欄を埋めよ．