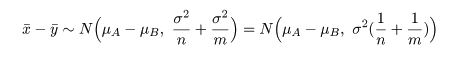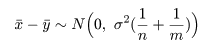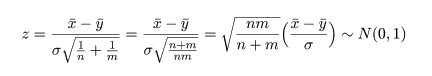2011.7.11

検定における２種類の過誤

検定は，仮説を棄却するか採択するかのいずれかであるが， 統計量は分布をもつので，この判定には間違いが起こることがある．
以下のように，この過誤には 2 種類がある．

統計的検定における2種類の過誤
  仮説の棄却 仮説の採択
仮説が真のとき 第１種の過誤 正解
仮説が偽のとき 正解 第２種の過誤

第１種の過誤が有意水準である．また，第２種の過誤の確率を β としたとき， 仮説が偽のとき正しく仮説を棄却する確率，1 - β，を検出力という． よい検定は，第１種の過誤を固定したもとで検出力の高い検定方式である．

検定における２種類の過誤のシミュレーション

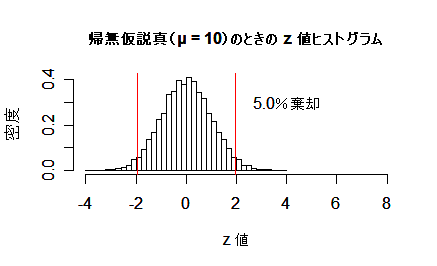
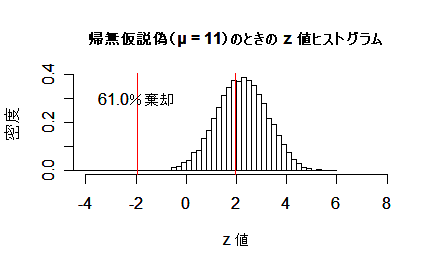
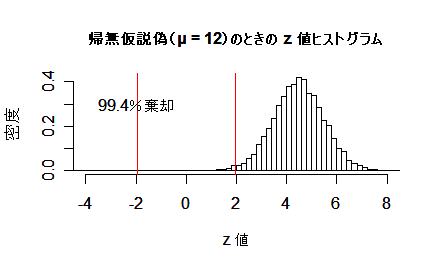
帰無仮説：H0：μ ＝ 10，の検定で第１種の過誤（タイプ１エラー）と 第２種の過誤（タイプ２エラー）の様子をシミュレーションでみる．すなわち，実際の母集団平均μを動かし， サンプルサイズを n = 20 として，多数（１万回）の検定を行う．

6-3．２つの母集団に対する検定（分散既知）

両側検定

　正規分布に従う２つの母集団 A，B があり，その母分散は等しく σ2 で既知であるとする． 母集団 A，B の母平均が μA，μB，であるとしたとき，

帰無仮説，H0： μA ＝ μB
対立仮説，H1： μA ≠ μB

の検定を行う．

　母集団 A から大きさ n，母集団 B から大きさ m の標本を抽出したところ， 母集団 A からの標本の標本平均が x-，母集団 B の 標本平均が y-，であったとしよう．
　母集団 A の標本分布は，N（μA，σ2）であり，母集団 B では， N（μB，σ2）であることから，それぞれの標本平均は，

x- 〜 N（μA，σ2/n）， y- 〜 N（μB，σ2/m）
と分布する．これより，標本平均の差x- − y- は，
と分布する．

帰無仮説（H0： μA = μB）のもとでは，μA−μB = 0，なので， 標本平均の差は，

と分布する．これを標準化した z 値は，
と標準正規分布するので，標準正規分布表を用いて検定が行える．すなわち，検定統計量 |z | に対し，

|z | ＞ 1.96 ⇒ 有意水準 5 ％で帰無仮説を棄却．
|z | ＞ 2.58 ⇒ 有意水準 1 ％で帰無仮説を棄却．

とすればよい．
例題
　通常の飼育方式と新方式による飼育方法で，鶏の１ヶ月の成長量に差があるか 調べたい．通常の飼育方式で 20 羽を飼育したところ，平均成長量が 100g， また，新方式による飼育方法を 25 羽で行ったところ，平均成長量が 105g であった． 新方式は通常の飼育方式と成長量が有意に異なるか 両集団の標準偏差は等しく 10g であることがわかっているとして検定せよ．
解答例
　新方式による成長量の母集団平均を μA とおき，通常の飼育方式の成長量の 母集団平均を μB とおく．
この問題での帰無仮説（H0）と対立仮説（H1）は，
H0： μA ＝ μB
H1：μA ≠ μB
と定式化される．
　通常方式のサンプルサイズが n = 20 なので，平均成長量 x- = 100g の分散は， σ2/n = 102/20 = 100/20 = 5 である．
　一方，新方式のサンプルサイズは m = 25 なので，その平均成長量 y- = 105g の分散は， 102/25 = 100/25 = 4 である．
　帰無仮説のもとでは，通常方式の平均と新方式の平均の差 x- - y- は， 平均 0，分散 100/20 + 100/25 = 9 の正規分布に従う．すなわち， x- - y- 〜 N(0，32) である．これを標準化すると，

z = (x- - y-)/3 = -5/3 = -1.67．
|z | ＝ 1.67 ＜ 1.96 ⇒ 帰無仮説は棄却されない

となる．すなわち，新方式は通常方式とは有意に異ならない．
Copyright (C) 2008, Hiroshi Omori. 最終更新：2011年 7月11日