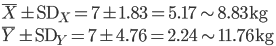2011.5.09
携帯解答サイト: http://lbm.ab.a.u-tokyo.ac.jp/~omori/k/
4-3.データのちらばりの程度を表す統計量
いま,2つの重量データ,
X = (5, 6, 8, 9)kg と
Y = (12, 4, 10, 2)kg があったとする.
X の標本平均
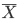
と Y の標本平均
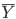
を計算してみると,
となりどちらも同じである.X と Y の違いをみると,X の方が Y よりもデータが平均値 7 に近い値をとっている,つまり,X の方が Y より個々のデータがより近い値を取っていることがわかる.これを表現する概念としてデータのちらばりがある.X の方が Y よりちらばりが小さい.これを表す値として分散や標準偏差がある.
標本分散: s2
n - 1:標本分散の自由度.データ数は
n で,データ全体では
n の自由度(値が自由に変われるデータの個数)を持つが,標本分散を計算するときに標本平均
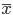
が固定されるので,自由度が 1 つ減って
n - 1 となった.
(標本)標準偏差(SD, Standard Deviation): s,
標本分散の平方根.平均と同じ単位で,データのちらばりの程度を表す.
-
重量データ X kg の分散と標準偏差を求めてみよう.
-
標本分散:
標本標準偏差:
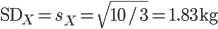
標本分散 s2 はデータの2乗を計算するので 3.33 kg2 と単位も kg の2乗となり標本平均と直接計算することはできないが,標準偏差 SD は 1.83 kg と標本平均 7 kg と
同じ単位をもつので直接計算することができる.すなわち,データの多くの部分が含まれる範囲を,
標本平均 ± 標準偏差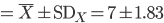
kg
と表すことができる.
ところで,標本分散は以下のように表でまとめると計算しやすい(と思う).
|
X の分散(平均 7)
|
データ
|
5
|
6
|
8
|
9
|
平方和
|
|
偏差
|
-2
|
-1
|
1
|
2
|
|
|
偏差平方
|
4
|
1
|
1
|
4
|
10
|
標本分散:s2X = 10/3 = 3.33
標準偏差:SD X = 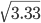 = 1.83
|
|
Y の分散(平均 7)
|
データ
|
12
|
4
|
10
|
2
|
平方和
|
|
偏差
|
5
|
-3
|
3
|
-5
|
|
|
偏差平方
|
25
|
9
|
9
|
25
|
68
|
標本分散:s2Y = 68/3 = 22.7
標準偏差:SD Y = 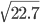 = 4.76
|
これより,
となり,X より Y の方が値の範囲が広いことが標準偏差の値で示される.
- 平均値,標本分散の計算
以下のデータの代表値を小数第2位まで(小数第3位まで求めて四捨五入する)求めよ.
計算には電卓等を用いてよい.解答は数値解答テストで送信(半角数字)
すること.
9,4,6,5,-4,2,-1, 3
第1問:メディアン(中央値)
第2問:平均値
第3問:偏差平方和
第4問:標本分散
第5問:標準偏差(SD)
計算用紙
| データ | 9 |
4 | 6 |
5 | -4 |
2 | -1 |
3 |
平方和 |
| 偏差 | | | | |
| | | |
|
| 偏差平方 | | | | |
| | | |
|
Copyright (C) 2010, Hiroshi Omori. 最終更新:2011年 5月08日
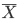 と Y の標本平均
と Y の標本平均 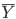 を計算してみると,
を計算してみると,
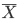 と Y の標本平均
と Y の標本平均 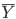 を計算してみると,
を計算してみると,
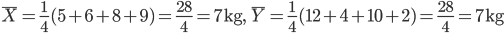
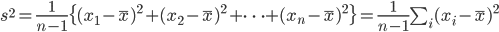
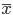 が固定されるので,自由度が 1 つ減って n - 1 となった.
が固定されるので,自由度が 1 つ減って n - 1 となった.
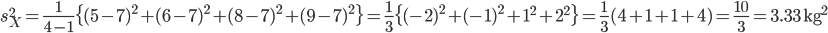
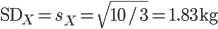
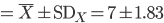 kg
kg
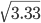 = 1.83
= 1.83
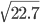 = 4.76
= 4.76