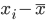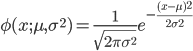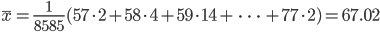統計学の基礎（0523）

携帯解答サイト： http://lbm.ab.a.u-tokyo.ac.jp/~omori/k/

2011.05.23

データの多くが存在する範囲の解答結果

第６問：ボリュームゾーン最低点
内訳	のべ解答数	解答者数	間違い	正　解
人数	61	35	29	32

第７問：ボリュームゾーン最高点
内訳	のべ解答数	解答者数	間違い	正　解
人数	40	30	8	32

第８問：メディアン
内訳	のべ解答数	解答者数	間違い	正　解
人数	60	36	29	31

第９問：四分位範囲の下限（25％点）
内訳	のべ解答数	解答者数	間違い	正　解
人数	105	31	86	19

第10問：四分位範囲の上限（75％点）
内訳	のべ解答数	解答者数	間違い	正　解
人数	35	22	14	21

4-4．形状の情報

単調減少（増加）型，単峰型，2峰型：ヒストグラムでわかる．
歪度（わいど）Skewness：歪度正→右に長く伸びる．歪度負→左に長く伸びる
尖度（せんど）Kurtosis：尖度 = 3 →正規分布と似た尖り．

データ分布（ヒストグラム）による標準偏差（SD）の違い

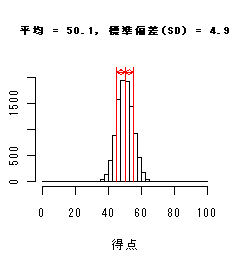
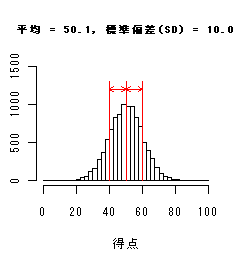
以下のヒストグラムは，平均値は同じだが標準偏差が異なっている．
標準偏差（SD）が小さいときは分布が平均のまわりに集中し，大きいときは分布が広がり，データのちらばりが大きくなっている．

単峰（つり鐘型）	単峰（つり鐘型）	単峰型
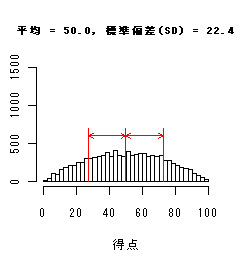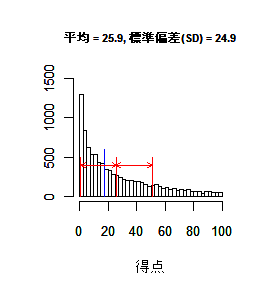
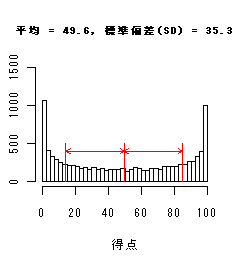
単調減少型メディアン（中央値）= 17.7，歪度＝1.1	U字型	2峰型
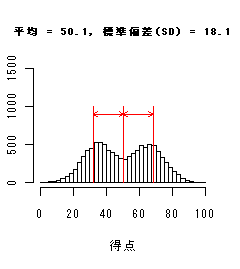
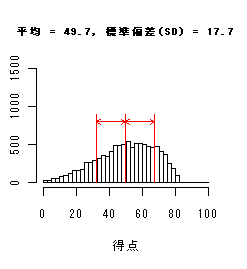
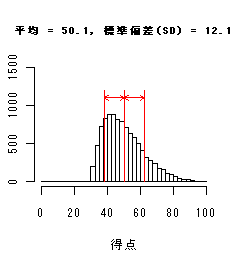
単峰型（左に裾が伸びる）歪度＝-0.43	単峰型（右に裾が伸びる）歪度＝0.45	単峰型（右に裾が伸びる）歪度＝0.80

4-5．データ操作

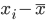
中心化：中心化データ＝データ－平均値＝ $x_i - \bar{x}$
データの偏差を取ること．中心化データの平均は 0．
標準化：標準化データ＝(データ－平均値)/標準偏差＝中心化データ/標準偏差

$z_i = \frac{x_i - \bar{x}}{\rm SD}$

標準化データ（z_i）の平均は 0，標準偏差は 1，（分散も1）．

データを標準化すると比較がしやすくなる．
（->偏差値：平均50，標準偏差10に得点を標準化したもの）

例題

　先々週取り上げたデータ

9，4，6，5，-4，2，-1, 3

の平均は 3，標準偏差は 4.1 であった．これより，データの最小値 -4 と最大値 9 の標準化した値を求めよ．

解答
最小値 -4 に対しては，(-4 - 3)/4.1 = -7/4.1 = -1.7
最大値 9 に対しては，(9 - 3)/4.1 = 6/4.1 = 2.195 = 2.2

あるクラスの英語得点と国語得点の代表値が以下の表のようであった．

	平　均	標準偏差
英　語	58.6点	11.6点
国　語	54.2点	16.0点

問題：A君の得点は英語，国語とも65点であった．

第11問：A 君の英語得点の標準化値（小数第２位）を，数値解答テスト第11問で送信せよ．

第12問：A 君の国語得点の標準化値（小数第２位）を，数値解答テスト第12問で送信せよ．

問：英語と国語，どちらの方が成績が良かったと言えるか．選択肢解答テスト第１問で送信せよ．

　１．国語の方がよい　　

　２．英語の方がよい　　

　３．国語と英語は同じ　

５. 正規分布

5-1．正規分布とは

　正規分布は，数量データの分布を表す最も重要な分布である．そのわけは，

身長，体重など正規分布に従うデータが多い（経験的知識）
どのような分布をもつ母集団からのサンプルであっても，データの平均値はデータ数を増やせば正規分布に近づく（中心極限定理）

平均 μ（ミュー），分散 σ²（シグマ 2 乗）の 2 つのパラメータ（母数）で形が決まる．
釣りがね型の分布
標準偏差 σ が小さいほど中心に集中した分布になる．
確率変数 x がこの正規分布に従うとき，x ～ N( μ，σ² )，と書く．
正規分布の密度関数は，以下の通り．

$\phi(x; \mu, \sigma^2)=\frac{1}{\sqrt{2\pi \sigma^2}} e^{-\frac{(x-\mu)^2}{2\sigma^2}}$

5-2．正規分布の形状

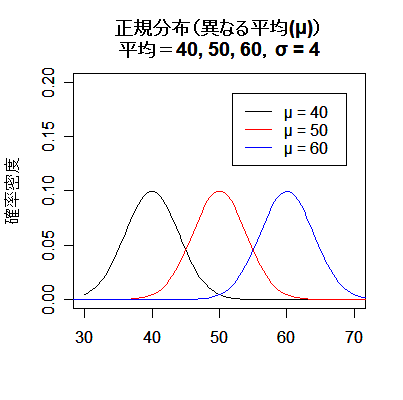
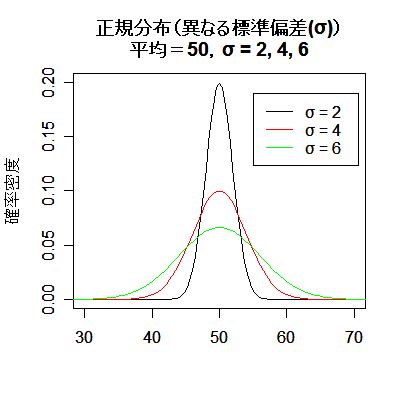
　平均 μ と分散 σ²（標準偏差 σ）の違いにより分布の形状がどのように異なるかをみてみよう．左下図をみると，平均 μ は分布の中心的な位置を表している．また右下図をみると，標準偏差 σ は分布の拡がりを表している．すなわち，σ が小さいと分布はより平均の近くに集まり，σ が大きいと分布は幅広い範囲に拡がる．

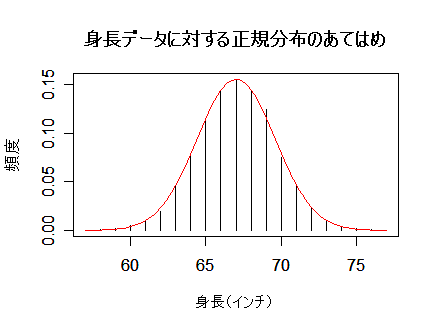
5-3．正規分布のあてはめ

　身長や体重などの身体データや得点データなどは正規分布に従うことが多い．たとえば，英国成人男子身長（インチ）のデータに正規分布をあてはめてみる．

**英国男子身長データ（インチ）**
身長	57	58	59	60	61	62	63	64	65	66
人数	2	4	14	41	83	169	394	669	990	1223
67	68	69	70	71	72	73	74	75	76	77
1329	1230	1063	646	392	202	79	32	16	5	2

まず，データから統計量を求める．データ総数は 8585 名である．

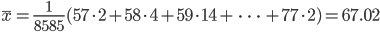
標本平均： $\bar{x} =\frac{1}{8585}(57 \cdot 2 + 58 \cdot 4 + 59 \cdot 14 + \ \cdots \ + 77 \cdot 2)=67.02$

標本分散： $s^2=\frac{1}{8584} \{ (57-67.02)^2 \cdot 2 + (58-67.02)^2 \cdot 4 + \ \cdots \ + (77-67.02)^2 \cdot 2 \} = 6.62$

これより，平均 μ ＝ 67.02，分散 σ² ＝ 6.62，の正規分布にあてはめ，赤線でグラフ表示したところ，上図のようにデータ分布によく一致していた．