統計学の基礎(5.30)

2011.5.30

携帯解答サイト： http://lbm.ab.a.u-tokyo.ac.jp/~omori/k/

5-4．標準正規分布 N (0, 1)

　平均 μ = 0，分散 σ² = 1（標準偏差 σ = 1）の正規分布を標準正規分布という．

標準正規分布累積確率表
z の値			0.0	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1.0
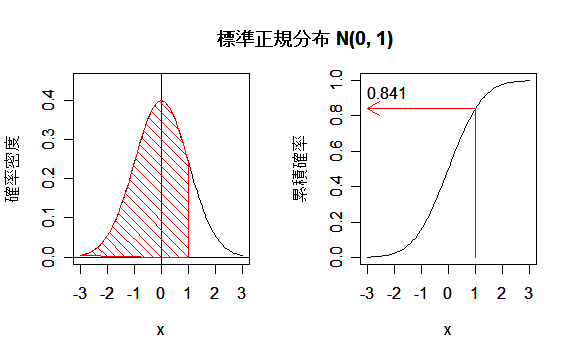
累積確率			0.500	0.540	0.579	0.618	0.655	0.691	0.726	0.758	0.788	0.816	0.841
1.1	1.2	1.3	1.4	1.5	1.6	1.64	1.7	1.8	1.9	1.96	2.0	2.58	3.0
0.864	0.885	0.903	0.919	0.933	0.945	0.95	0.955	0.964	0.971	0.975	0.977	0.995	0.999

標準正規分布累積表の使い方１（小数第１位）
以下のデータの代表値を小数第１位まで（小数第２位まで求めて四捨五入する）求めよ．計算には電卓等を用いてよい．解答は数値解答テスト２で送信(半角数字) すること．
第13問：標準正規分布 N(0, 1) で，1以上にデータの何％を含むか．
第14問：標準正規分布で，-0.5以下にデータの何％を含むか．
第15問：標準正規分布で，-1.96から1.96までの間にデータの何％を含むか．

　正規分布との関係は以下の通り．

正規分布     標準正規分布

平均：μ，分散：σ²         平均：0，分散：1

標準偏差：σ 標準偏差： 1
x ～ N (μ，σ² )     z ～ N (0，1)

     $z = \frac{x-\mu}{\sigma}$      $x = \mu + z \cdot \sigma$

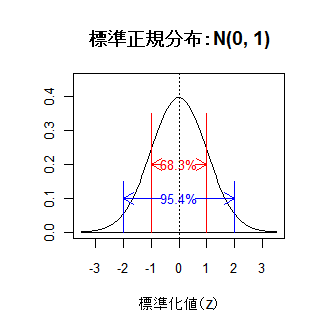
標準正規分布 N(0, 1) では，-1 ≦ z ≦ 1 の範囲に全体の68.3％が含まれ， -2 ≦ z ≦ 2 の範囲に全体の95.4％が含まれる（下左図）．
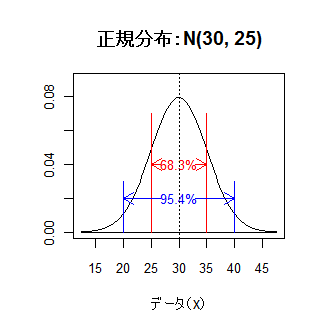
　また，平均 μ - 30，分散 25 の正規分布 N(30, 25) では，標準偏差が σ = √25 = 5 なので， 25 ≦ x ≦ 35 の範囲に全体の68.3％が含まれ， 20 ≦ x ≦ 40 の範囲に全体の95.4％が含まれる（下右図）．

範囲に含まれる確率
N(0, 1)	N(30, 25)	N(μ，σ²)	確率(％)
-1 → 1	25 → 35	μ - σ → μ + σ	68.3
-1.96 → 1.96	20.2 → 39.8	μ - 1.96σ → μ + 1.96σ	95.0
-2 → 2	20 → 40	μ - 2σ → μ + 2σ	95.4
-2.58 → 2.58	17.1 → 42.9	μ - 2.58σ → μ + 2.58σ	99.0
-3 → 3	15 → 45	μ - 3σ → μ + 3σ	99.7

例題: 標準正規分布では，-2から2までの間に全データのかなりの部分（95.4%）が含まれる．平均 8，分散 4 の正規分布でこの区間に対応するのは何か．; 平均μ＝8，標準偏差σ＝√4＝2．
小さい値＝μ－2σ＝8－2*2＝4，大きい値＝μ＋2σ＝8＋2*2＝12．これより，4 ～ 12，に全データのかなりの部分が含まれる．

標準正規分布累積表の使い方２（小数第１位）
以下のデータの代表値を小数第１位まで（小数第２位まで求めて四捨五入する）求めよ．計算には電卓等を用いてよい．解答は数値解答テスト２で送信(半角数字) すること．

第16問：平均50点，標準偏差10点の正規分布で，35点以上にデータの何％を含むか．

第17問：平均50点，標準偏差10点の正規分布で，上位5％以内に入るには何点（整数）あればよいか．

第18問：1万人が受けたテストの平均は50点，標準偏差は10点であった．70点の学生の順位．