統計学の基礎(6.6)

2011.6.6

携帯解答サイト： http://lbm.ab.a.u-tokyo.ac.jp/~omori/k/

5-5．正規分布へのあてはまりのよさと Q - Q プロット

　以前，取り上げた英語得点データに正規分布をあてはめてみる．英語得点データの代表値は，

平均：58.6点，標準偏差：11.6点（分散：134.4）

であったので，平均 μ = 58.6，分散 σ² = 134.4 の正規分布，

N(58.6, 134.4)

にあてはめればよい．

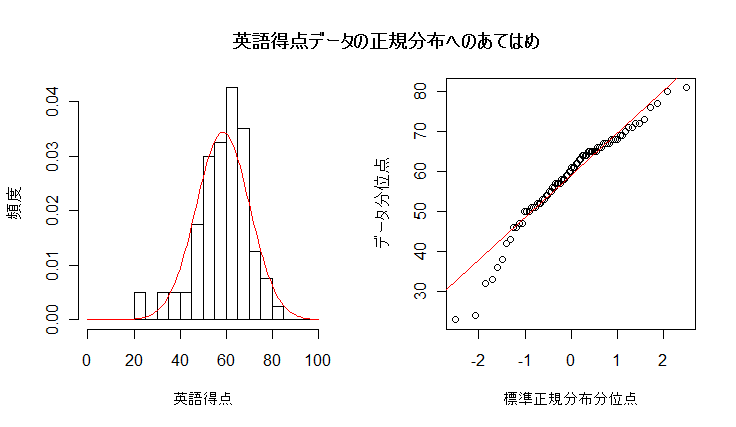
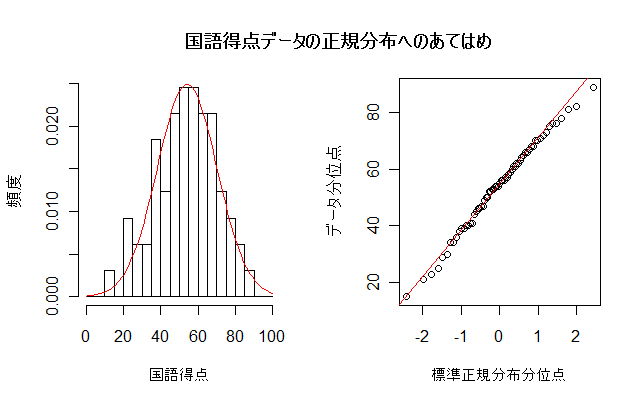
　データが正規分布によくあてはまっているかを視覚的にみる方法として，Q - Q プロットがある．
　これは，標準正規分布とデータの分位点との関係を図示したもので，これが，直線上に乗っているとデータが正規分布によくあてはまっていることがわかる．
　このプロットを手でつくるのは難しいので，ソフトウエアで書かせる．ここでは，Q - Q プロットで正規分布へのあてはまりのよさがわかることを覚えておけば十分である．

　国語得点データに正規分布をあてはめると，

平均：54.2点，標準偏差：16.0点（分散：255.3）

であったので，平均 μ = 54.2，分散 σ² = 255.3 の正規分布，

N(54.2, 255.3)

にあてはめる．

問：英語と国語，どちらの方が正規分布へのあてはまりがよいと言えるか．選択肢解答テスト第２問で送信せよ．

　１．国語の方がよい　　

　２．英語の方がよい　　

　３．国語と英語は同じ　

5-6. 独立な正規分布の合成分布

平均 μ₁，分散 σ₁²，の正規分布からの標本 x ～ N( μ₁，σ₁² ) と，平均 μ₂，分散 σ₂²，の正規分布からの標本 y ～ N( μ₂，σ₂² ) があり，両者が互いに独立であるとする．（y の値は x の値の影響を受けない．）

和の分布 x ＋ y は平均 μ₁ ＋ μ₂，分散 σ₁² ＋ σ₂²，の正規分布に従う．
x ＋ y ～ N（ μ₁ ＋ μ₂， σ₁² ＋ σ₂² ）差の分布 x － y は平均 μ₁ － μ₂，分散 σ₁² ＋ σ₂²，の正規分布に従う．
x － y ～ N（ μ₁ － μ₂， σ₁² ＋ σ₂² ）一般の線形結合の分布 a と b を任意の実数（スカラー）とすると，x と y の線形結合 ax ＋ by は，
ax ＋ by ～ N（ aμ₁ ＋ bμ₂， a² σ₁² ＋ b² σ₂² ）

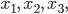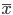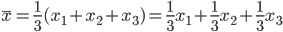
例題平均 μ 分散 σ² の正規分布から無作為標本（ランダムサンプル）， $x_1, \ x_2, \ x_3, \$ を抽出した．標本平均 $\bar{x}$ の分布を求めよ．: 解答例 $\bar{x}=\frac{1}{3}(x_1 + x_2 + x_3) = \frac{1}{3}x_1 + \frac{1}{3}x_2 + \frac{1}{3}x_3$
である．これより，
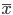標本平均 $\bar{x}$ の平均： ${\rm E}[\bar{x}]=\frac{1}{3}\mu+\frac{1}{3}\mu+\frac{1}{3}\mu=\mu$
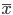標本平均 $\bar{x}$ の分散： ${\rm Var}[\bar{x}]= \bigl(\frac{1}{3} \bigr)^2 \sigma^2+\bigl(\frac{1}{3} \bigr)^2 \sigma^2+\bigl(\frac{1}{3} \bigr)^2 \sigma^2=\frac{1}{3}\sigma^2$
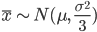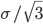よって， $\bar{x}\sim N(\mu, \ \frac{\sigma^2}{3})$ ．標準偏差（標準誤差）は $\sigma/\sqrt{3}$ ．
なお，標本平均のような統計量（標本から計算して得られる値）の標準偏差を標準誤差 （SE : standard error）という．
標準誤差は，標本平均の値がどれくらい振れる可能性があるかを示す指標となる．

正規分布からの標本（サンプル）の平均値の分布 平均 μ，分散 σ² の正規分布から大きさ n の標本を抽出
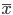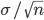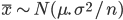→ 標本平均 $\bar{x}$ は平均 μ，分散 σ²/n （標準偏差 $\sigma/\sqrt{n}$ ）の正規分布に従う． $\bar{x} \sim N(\mu. \ \sigma^2/n)$ ．
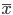→ 標本の大きさ（サンプルサイズ）を大きくすれば，母集団平均 μ は標本平均 $\bar{x}$ で精度よく推定できる．