2011.06.13
携帯解答サイト: http://lbm.ab.a.u-tokyo.ac.jp/~omori/k/
標本平均の分布
母集団とは日本全国の大学生の集合の英語の実力など,ある特性を調べたい集団全体を表す.
いま,正規分布 N(μ,σ2) に従う母集団を考える.すなわち,母平均が μ であり,母分散が σ2 である.
母平均などの母数を調べるため母集団から大きさ n の無作為標本(ランダムサンプル) x1,x2,…,xn を抽出したとする.
個々のサンプル xi はそれぞれ平均 μ 分散 σ2 の正規分布に従っている.これを,xi ~ N(μ,σ2),と表記する.
このとき,標本平均
が従う分布を考える.
まず,n = 2 のときから考えてみる.2 つのサンプルの標本平均を
と表すことにする.
x1 の平均が μ,分散が σ2 なので,これを E[x1] = μ,Var[x1] = σ2,と表記する.
同様に,x2 の平均も μ,分散も σ2 なので,これも E[x2] = μ,Var[x2] = σ2,と表記する.
すると,x1 + x2 の平均と分散はそれぞれ,
E[x1 + x2] = E[x1] + E[x2] = 2μ,Var[x1 + x2] = Var[x1] + Var[x2] = 2σ2
となる.よって,
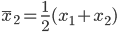
の平均は,
となる.分散は,2 乗の平均なので外に出すときは係数は 2 乗して,
となる.同様に考えると,
n 個のサンプルの標本平均
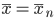
の平均と分散は,それぞれ,
となることがわかる.すなわち,標本平均
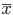
が従う分布は,
となる.
-
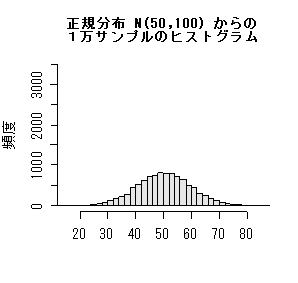
正規分布からの標本平均の分布
平均 μ = 50,分散 σ
2 = 100(標準偏差 σ = 10)の正規分布から大きさ n = 20 の標本を抽出.
|
|
データ例
|
標本平均 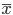
|
|
サンプル1:
|
46.44173, 55.98069, 60.65703, 57.35829, 29.06341, 55.92665, …
|
50.46604
|
|
サンプル2:
|
56.49328, 26.15988, 36.63778, 30.11928, 32.55220, 49.38015, …
|
47.40793
|
|
サンプル3:
|
42.89847, 45.66345, 54.59994, 34.18581, 43.40348, 51.62797 …
|
51.13295
|
|
…
|
…………………
|
…
|
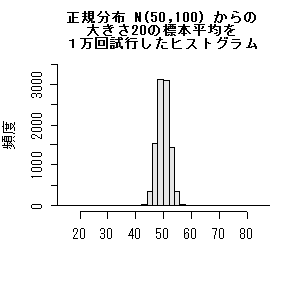
上の表のようにサンプルを多数回抽出したとすると,サンプルごとに標本平均が得られるので,標本平均の分布を考えることができる.
標本平均の分布の平均は,μ = 50,分散は,σ
2/n = 100/20 = 5(標準偏差 = √5 = 2.236)の正規分布になる.つまり,
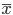
~ N(50, 5),
である.
-
例題 N(50, 100) から大きさ 20 の標本を抽出した.52.24 以上の標本平均が得られる確率は.
-
解答例 標本平均は,
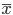
~ N(50, 5) と分布する.標準化の式より,
(値 - 平均)/標準偏差 = (52.24 - 50)/2.24 = 1
これより標準正規分布で z > 1,となる確率を求める.すなわち,
Pr[z > 1] = 1 - Pr[z < 1] = 1 - 0.841 = 0.159
- 問題:
標本平均の分布
-
平均 30 標準偏差 8 の正規分布から大きさ 25 の標本を抽出した.
以下の問に小数第1位までで答えよ.解答は数値解答テスト2で送信(半角数字) すること.
第19問:標本平均の標準偏差(標準誤差)
第20問:標本平均が 27.38 以下になる確率
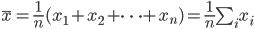
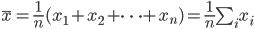
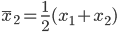
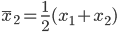 の平均は,
の平均は,
![{\rm E}[\bar{x}_2] = {\rm E}[\frac{1}{2}(x_1 +x_2)] = \frac{1}{2}{\rm E}[x_1 +x_2]=\frac{1}{2} \cdot 2\mu=\mu](images/EXTERN_0002.png)
![{\rm Var}[\bar{x}_2] = {\rm Var}[\frac{1}{2}(x_1 +x_2)] = \frac{1}{2^2}{\rm Var}[x_1 +x_2]=\frac{1}{4} \cdot 2\sigma^2=\frac{\sigma^2}{2}](images/EXTERN_0003.png)
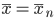 の平均と分散は,それぞれ,
の平均と分散は,それぞれ,
![{\rm E}[\bar{x}] = \mu, \ {\rm Var}[\bar{x}] =\frac{\sigma^2}{n}](images/EXTERN_0005.png)
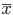 が従う分布は,
が従う分布は,
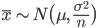
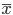
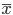 ~ N(50, 5),
~ N(50, 5),
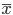 ~ N(50, 5) と分布する.標準化の式より,
~ N(50, 5) と分布する.標準化の式より,