2011.06.20
講義プリントサイト:http://lbm.ab.a.u-tokyo.ac.jp/~omori/kokusai11/
携帯解答サイト: http://lbm.ab.a.u-tokyo.ac.jp/~omori/k/
いままでのまとめ
統計学の考え方はなじみにくいと考えられるので,ここで,今までの内容を再確認して
何を行おうとしているのかを明らかにしたい.
1.正規母集団
今のところ,身長や体重,試験の得点などの数量的データを取り扱っている.
個々人のある数量的データを X とおく.対象となっている個体をすべて集めた集団
を母集団という.
母集団の個々人のデータの詳細は不明であるが,
個々の X を集めるとある釣り鐘型の分布になっていると考える.
この分布の平均を μ,分散を σ2 とすると,これを正規(Normal)分布
N(μ,σ2) という.また,σ を標準偏差(SD : Standard Deviaton)という
このように,正規分布に従っている母集団を,
正規母集団といい,この母集団の平均を特に母平均,分散を母分散と呼ぶこともある.
また,母平均 μ,母分散 σ2 を合わせて母集団の母数(パラメータ)
と呼ぶ.
これを,
X ~ N(μ,σ2),μ:(母)平均,σ2:(母)分散
と表記する.
2.標準正規分布,N(0,1)
平均 0,分散 1 の正規分布 N(0,1) を標準正規分布という.標準正規分布のときは,Z を
用いることが多い.すなわち,
Z ~ N(0,1),
と表記する.
この分布のある範囲に対する確率は,
標準正規分布で,Z が 1 以下になる確率(Probability) → Pr[ Z ≦ 1 ]
のように表記する。標準正規分布では,ある値 z ≧ 0 に対して,Pr[ Z ≦ z ] の値が
標準正規分布累積確率表で以下のように与えられている.
これより,たとえば,
Z が 1 以下になる確率 → Pr[ Z ≦ 1 ] = 0.841 (84.1%)
であることがわかる.正規分布分布全体での確率が 1 であるので,
Z が 1 以上になる確率 → Pr[ Z ≧ 1 ] = 1 - Pr[ Z ≦ 1 ]
= 1 - 0.841 = 0.159 (15.9%)
である.また,正規分布が左右対称であるので,負の z に対しては,
Z が -1 以上になる確率 → Pr[ Z ≧ -1 ] = Pr[ Z ≦ 1 ] = 0.841
であり,また,
Z が -1 以下になる確率 → Pr[ Z ≦ -1 ] = Pr[ Z ≧ 1 ]
= 1 - Pr[ Z ≦ 1 ] = 1 - 0.841 = 0.159
のように求めることができる.詳しい表を用いれば標準正規分布の任意の範囲に入る確率が求められる.
3.正規分布 N(μ,σ2) の確率計算
平均 μ,分散 σ2 の正規分布の場合,
X が x 以下になる確率 Pr[ X ≦ x] は,
の式で x を標準化して z に変換し,
Pr[ Z ≦ z ] に対応させれば求められる.
たとえば,平均 μ = 50,分散 σ2 = 102(標準偏差 σ = 10)の
正規分布 N(50,102) の場合を考えてみる.この分布から得られるデータを X とおくと,
X ~ N(50,102)
と書ける.ここで,
X が 65 以下になる確率 → Pr[ X ≦ 65 ]
を求めてみよう.このとき,x = 65 であるから,標準化により z に変換する.すなわち,
である.z にすれば標準正規分布表により確率計算ができる.よって
X が 65 以下になる確率 → Pr[ X ≦ 65 ] = Pr[ Z ≦ 1.5 ] = 0.933
である.また,
X が 35 以下になる確率 → Pr[ X ≦ 35 ]
では,標準化により
となるので,
X が 35 以下になる確率 → Pr[ X ≦ 35 ] = Pr[ Z ≦ -1.5 ]
= Pr[ Z ≧ 1.5 ] 1 - Pr[ Z ≦ 1.5 ] = 1 - 0.933 = 0.067
と求められる.このように,どのような正規分布でも標準化により標準正規分布に変換
すれば任意の範囲の確率計算を行うことができる.
4.母集団平均の推定とその精度
母集団の平均や分散などの母数がわかっている場合は少ない.このため,
母数の推定をどのように行うのがよいか考え,その精度を見積もることが
統計学の大きな課題である.
まず,母分散の値はわかっているが,母平均の値がわかっていないときを考える.
母平均を推定するために母集団から大きさ n の無作為標本(ランダムサンプル)を抽出する.
これを,
大きさ n の無作為標本:
X1,X2,…,Xn
と表記する.
母平均 μ は標本の標本平均,
で推定する.標本平均 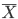 は,抽出する標本により値が変わるので,どれくらい動くのかを考えて精度評価を行う必要がある.
は,抽出する標本により値が変わるので,どれくらい動くのかを考えて精度評価を行う必要がある.
個々の標本 Xi は平均 μ 分散 σ2 の正規分布に従うが,標本平均
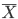 は以前示したように,平均 μ 分散 σ2/n の正規分布に従う.
は以前示したように,平均 μ 分散 σ2/n の正規分布に従う.
標本平均 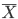 の標準偏差は
の標準偏差は 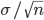 となるので,これが母平均 μ を標本平均
となるので,これが母平均 μ を標本平均
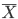 で推定したときの誤差の大きさを表していると考えられる.
で推定したときの誤差の大きさを表していると考えられる.
このため, 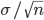 を標本平均
を標本平均 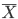 の標準誤差(SE : Standard Error)という.すなわち,
である.すなわち,母平均μを大きさnの標本の標本平均
の標準誤差(SE : Standard Error)という.すなわち,
である.すなわち,母平均μを大きさnの標本の標本平均
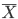 で推定すると,
で推定すると,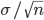 程度の推定誤差があると見積もれる.
程度の推定誤差があると見積もれる.
- 例題1
- 平均 μ = 50,標準偏差 σ = 10 の正規母集団から大きさ n = 25 の無作為標本を抽出した.
問1:標本平均の標準誤差はいくらか.
問2:標本平均が46以下になる確率はいくらか.
- 解答
-
問1:標本平均の標準誤差 SE = σ/√n = 10/√25 10/5 = 2
問2:x = 46 を標準化すると,
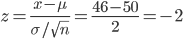
標本平均 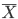 が 46 以下の確率 → Pr[
が 46 以下の確率 → Pr[
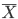 ≦ 46 ]
= Pr[ Z ≦ -2 ] = Pr[ Z ≧ 2 ] = 1 - Pr[ Z ≦ 2 ] = 1 - 0.977 = 0.023 (2.3%)
≦ 46 ]
= Pr[ Z ≦ -2 ] = Pr[ Z ≧ 2 ] = 1 - Pr[ Z ≦ 2 ] = 1 - 0.977 = 0.023 (2.3%)
であり,大きさ n = 25 の標本平均が 46 より小さくなることはあまりないことがわかる.
- 例題2
-
平均 μA = 50,標準偏差 σA = 10 の正規母集団 A から
大きさ nA = 25 の無作為標本を抽出し,
標本平均 X-A を出した.
一方,平均 μB = 45,標準偏差 σB = 9 の正規母集団 B から
大きさ nB = 9 の無作為標本を抽出し,
標本平均 X-B を出した.
このとき,X-B が X-A より
大きくなる確率を求めよ.
- 解答
-
X-A の標準誤差 SEA =
σA/√nA = 10/√25 = 2
→ X-A ~ N(50, 4)
X-B の標準誤差 SEB =
σB/√nB = 9/√9 = 3
→ X-B ~ N(50, 9)
Y = X-B - X-A の平均:
μB - μA = -5,
X-B - X-A の分散:
σA/nA + σB/nB = 4 + 9 = 13
これより,Y の分布は,Y ~ N(-5, 13)
X-B > X-A →
Y > 0 なので,Pr[ X-B > X-A ]
= Pr[ Y > 0 ]
y = 0 を標準化すると,z = {0 - (-5)}/√13 = 5/3.6 = 1.39 ≒ 1.4
Y が 0 より大きくなる確率 → Pr[ Y > 0 ] ≒ Pr[ Z > 1.4 ] =
1 - Pr[ Z < 1.4 ] = 1 - 0.919 = 0.081 (8.1%)
Copyright (C) 2008, Hiroshi Omori. 最終更新:2011年 6月19日
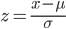
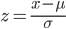
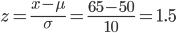
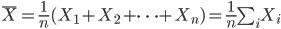
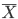 は,抽出する標本により値が変わるので,どれくらい動くのかを考えて精度評価を行う必要がある.
は,抽出する標本により値が変わるので,どれくらい動くのかを考えて精度評価を行う必要がある.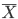 は以前示したように,平均 μ 分散 σ2/n の正規分布に従う.
は以前示したように,平均 μ 分散 σ2/n の正規分布に従う.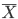 の標準偏差は
の標準偏差は 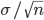 となるので,これが母平均 μ を標本平均
となるので,これが母平均 μ を標本平均
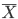 で推定したときの誤差の大きさを表していると考えられる.
で推定したときの誤差の大きさを表していると考えられる.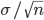 を標本平均
を標本平均 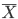 の標準誤差(SE : Standard Error)という.すなわち,
の標準誤差(SE : Standard Error)という.すなわち,
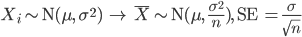
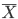 で推定すると,
で推定すると,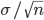 程度の推定誤差があると見積もれる.
程度の推定誤差があると見積もれる.
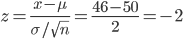
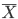 が 46 以下の確率 → Pr[
が 46 以下の確率 → Pr[
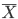 ≦ 46 ]
= Pr[ Z ≦ -2 ] = Pr[ Z ≧ 2 ] = 1 - Pr[ Z ≦ 2 ] = 1 - 0.977 = 0.023 (2.3%)
≦ 46 ]
= Pr[ Z ≦ -2 ] = Pr[ Z ≧ 2 ] = 1 - Pr[ Z ≦ 2 ] = 1 - 0.977 = 0.023 (2.3%)