2011.06.27
5-7. 正規分布に基づく母数の区間推定
分散既知の場合の母平均 μ の区間推定
正規分布する母集団で分散がわかっている場合は,未知の平均に関する区間推定ができる.
いま,正規分布
N(
μ,σ
2) において,大きさ
n の標本を抽出したとき,標本平均
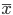
は,
と分布する.標準正規分布の 97.5%分位点は 1.96 であるので,標準正規分布する確率変数 z が -1.96 から 1.96 に入る確率は 0.95 となる.つまり
となる.最後の式を母集団平均 μ の 95% 信頼区間と言う.
このように,母数の信頼区間を標本から推定することを区間推定という.
- 例題
-
過去の経験から分散が 9 であることがわかっている正規母集団から大きさ 16 の標本を抽出
したところ,標本平均が 1.5 であった.標準正規分布の 97.5% 分位点を 1.96
として,母平均 μ の 95% 信頼区間を求めよ.
- 解答例
-
σ=√9=3,√n=√16=4,より,1.96×σ/ √n=1.96×3/4=1.47
よって,1.5 ± 1.47,つまり, 0.03 < μ < 2.97 が母平均 μ の 95% 信頼区間
となる.
95% の意味
同じ正規母集団から標本抽出を繰り返すと,毎回標本平均として異なる値がえられ,それに
対応して信頼区間も異なる.この信頼区間の 95% が真の平均 μ を含む,という意味である.
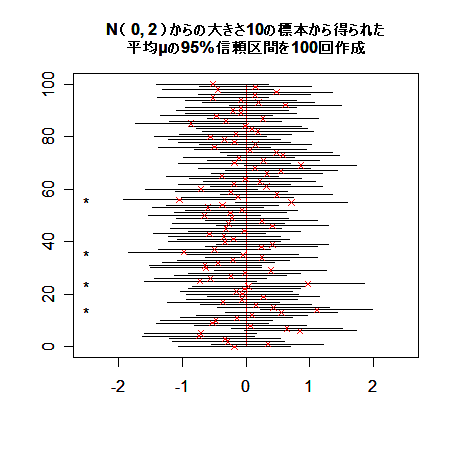
つまり,100回の標本抽出により,100 個の信頼区間を作ったら平均的にみて,95 個の信頼区間が
真の平均 μ を含むことが期待できる.
下の図は,平均 0 分散 2 の正規分布 N( 0, 2 ) から大きさ 10 の標本を取りだし,分散が既知であるとして,
母平均に対する信頼区間を 100 個生成したものである."×" が標本平均を示す.左の "*" は,信頼区間
が母平均の真値 0 を含まなかった場合である.
Copyright (C) 2008, Hiroshi Omori. 最終更新:2011年 6月26日
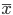 は,
は,
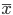 は,
は,
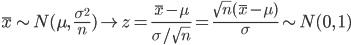
![{\rm Pr}[-1.96<z<1.96]=0.95](images/EXTERN_0002.png)
![{\rm Pr}[-1.96<\frac{\sqrt{n}(\bar{x}-\mu)}{\sigma}<1.96] = 0.95](images/EXTERN_0003.png)
![{\rm Pr}[-1.96\cdot \frac{\sigma}{\sqrt{n}} <\bar{x}-\mu<1.96\cdot \frac{\sigma}{\sqrt{n}} ] = 0.95](images/EXTERN_0004.png)
![{\rm Pr}[-1.96\cdot \frac{\sigma}{\sqrt{n}} <\mu-\bar{x}<1.96\cdot \frac{\sigma}{\sqrt{n}} ] = 0.95](images/EXTERN_0005.png)
![{\rm Pr}[\bar{x}-1.96\cdot \frac{\sigma}{\sqrt{n}}<\mu<\bar{x}+1.96\cdot \frac{\sigma}{\sqrt{n}}]=0.95](images/EXTERN_0006.png)
![{\rm Pr}[\bar{x}-d<\mu<\bar{x}+d]=0.95, \ d=1.96\cdot \frac{\sigma}{\sqrt{n}}](images/EXTERN_0007.png)