2011.07.04
6.仮説検定
6-1.帰無仮説(H0)と対立仮説(H1)
統計的仮説
統計学で扱う仮説とは,母集団に対する断定や推測.たとえば,
- 母集団は正規分布に従っている.
- 母集団平均は 0 である.
- 母集団 A と母集団 B の平均は等しい.
などである.
統計的仮説検定で用いられる仮説は,まず,帰無仮説という形式で与えられる.
帰無仮説は棄却されることに意味がある仮説である.
帰無仮説と反対の仮説を対立仮説という.
上の3番目の例でみると,
帰無仮説:
母集団 A と母集団 B の平均は等しい.
(H0: μA = μB)
対立仮説:
母集団 A と母集団 B の平均は等しくない.
(H1: μA ≠ μB)
母集団 A と母集団 B は異なる処理(薬の投与など)をしているので,実験の目的
は,母集団 A と母集団 B の平均は異なる(処理効果がある)ことを言いたい
(対立仮説が正しいことを望む)のだが,まずは
「等しい(処理効果無し)」と仮定してみようという考え方.
6-2.検定
検定統計量
標本から算出される量で,検定に用いられるもので,z 値,t 値,χ2 値
(後で定義する)などがある.
この値から帰無仮説を受託(採択)するか
棄却(対立仮説の採択)するかを判定する.
有意水準
統計的仮説検定では,たとえば2つの母集団平均が等しいという帰無仮説を考えると,
この帰無仮説のもとで,検定統計量(標本平均の差に基づく t 値など)以上
(もしくは未満)の値が得られる確率を求める.
くだけた言い方をすれば,帰無仮説が正しいとしたときに,標本のようなデータが得られる確率
を求める.
これが十分小さい(ほとんどありえない)ときは,平均が等しいと仮定したことが誤りであったと判断して
帰無仮説を棄却し,2つの母集団平均には差があると結論づける.
この確率がそれほど小さく
ない場合は,このような統計量が得られることもありえると考え,帰無仮説を採択し,平均が等しいと考え
てもよいとする.
棄却か採択かの判断の基準となる確率を有意水準といい,
5 % や 1 % がよく用いられる.
- 例題
- 通常の飼育方式では,鶏の1ヶ月の成長量が平均 100g,標準偏差 10g であることが知られて
いるとする.新方式 A による飼育方法を 25 羽で試したところ,平均成長量が 105g となった.新方式
でも標準偏差は変わらないものとして,新方式 A は通常の飼育方式と成長量が有意に異なるか
検定せよ.ただし,以下の標準正規分布の分位点(パーセント点)を用いよ.
検定に用いられる標準正規分布の
分位(パーセント)点
| 確率 |
0.95 | 0.975 |
0.99 | 0.995 |
| 分位点 |
1.64 | 1.96 |
2.33 | 2.58 |
- 解答例
- 新方式による成長量の母集団平均を μ とおき,通常の飼育方式の成長量の
母集団平均を μ0 = 100 とおく.題意より,新方式での成長量の標準
偏差は,通常の飼育方式と等しい σ = 10 とみなせる.
この問題での帰無仮説(H0)と対立仮説(H1)は,
H0:μ = μ0
H1:μ ≠ μ0
と定式化される.検定に用いる検定統計量は,標本平均を標準化した z 値の絶対値
である.
標本の大きさ n = 25 の標本の標本平均
 = 105より,
である.新方式の標本平均の標準化値の絶対値 |z | = 2.5 は,両側 5 %点(片側 2.5 %点)
の 1.96 よりは
大きく,両側 1 %点(片側 0.5 %点)の 2.58 よりは小さい.
= 105より,
である.新方式の標本平均の標準化値の絶対値 |z | = 2.5 は,両側 5 %点(片側 2.5 %点)
の 1.96 よりは
大きく,両側 1 %点(片側 0.5 %点)の 2.58 よりは小さい.
よって,新方式は通常方式と成長量は 5 %水準で有意に異なると言えるが,1 %水準
では有意でない.つまり,5 %有意である.
検定の結論の書き方
- 有意でない → 5 %で帰無仮説が棄却できないとき.
- 5 %有意 → 5 %で帰無仮説が棄却できたが 1 %では棄却できなかったとき.
- 1 %有意 → 1 %で帰無仮説が棄却できたとき.
片側検定と両側検定
実験状況によっては,薬投与などの処理を行った集団(処理群)平均
μA が,薬を投与しない
集団(対照群)の平均 μB より小さくなることはないことが事前に
わかっているような場合が
ある.このようなとき,
帰無仮説,H0: μA =
μB
対立仮説,H1: μA >
μB
となる.これは,事前情報より,μA < μB となる可能性
をまったく考えない場合である.
このため検定には,片側 5 %点や 1 %点を用いる.
- 例題
- 通常の飼育方式では,鶏の1ヶ月の成長量が平均 100g,標準偏差 10g であることが知られて
いるとする.改良方式 B による飼育方法を25羽で試したところ,平均成長量が 103.5g となった.
改良方式は,通常方式より成長量が減少することがないことが知られている.
改良方式での標準偏差は変わらないものとして,改良方式 B は通常の飼育方式と
成長量が有意に増大したか
検定せよ.ただし,例題の標準正規分布の分位点(パーセント点)を用いよ.
- 解答例
- 改良方式による成長量の母集団平均を μ' とおき,通常方式の成長量の
母集団平均を μ0 =100とおく.題意より,改良方式での成長量の標準
偏差は,通常の飼育方式と等しい σ = 10 とみなせ,また,
改良方式平均 μ' は通常方式平均 μ0 より
下回ることは想定されない.よって,対立仮説は片側となり,
この問題での帰無仮説(H0)と対立仮説(H1)は,
H0:μ' = μ0
H1:μ' > μ0
と定式化される.検定に用いる検定統計量は,標本平均を標準化した z 値
である.
標本の大きさ
n = 25 の標本の標本平均

= 103.5より,
よって,改良方式は通常方式と成長量は 5 %水準で有意に増大したと言えるが,1 %水準
では有意でない.
両側検定であれば,5 %水準でも有意にならなかったことに注意.つまり,改良方式と通常方式
の間には有意な差はみとめられなかった,という結論になった.片側検定の方が有意な結果
が出やすい.
両側検定と信頼区間
母集団平均に対する両側検定は,母集団平均に対する信頼区間と大きな関係がある.
いま,帰無仮説(H0)と対立仮説(H1)が,
H0:μ = μ0
H1:μ ≠ μ0
であり,母分散 σ2 が既知のときを考える.
標本の大きさが
n で,標本平均が

であったとすると,
|
個々の標本 xi は,平均 μ,分散 σ2 の正規分布に従う.
→ xi ~ N(μ, σ2 )
|
標本平均
 は,平均 μ,分散 σ2/n の正規分布に従う.→
は,平均 μ,分散 σ2/n の正規分布に従う.→
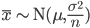
|
これを標準化した z は,標準正規分布に従う.→

|
母平均 μ に対する 95%信頼区間は,
となる.
一方,この検定の検定統計量は,標本平均の標準化値の絶対値
で,有意水準 5 %で帰無仮説を受諾するのは,検定統計量 |z| が両側 5 %点である 1.96 以下のときである.つまり,
|
帰無仮説を受諾 ⇔
|

|
である.この両者の関係より,
帰無仮説を受諾 ⇔ 母平均の信頼区間に μ0 が含まれる.
帰無仮説を棄却 ⇔ 母平均の信頼区間に μ0 が含まれない.
が成り立つ
Copyright (C) 2008, Hiroshi Omori. 最終更新:2011年 7月 3日
 = 105より,
= 105より,

 = 105より,
= 105より,

 = 103.5より,
= 103.5より,
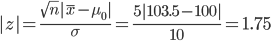
 であったとすると,
であったとすると,
 は,平均 μ,分散 σ2/n の正規分布に従う.→
は,平均 μ,分散 σ2/n の正規分布に従う.→
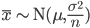

![{\rm Pr} \Bigl[ -1.96 < \frac{\sqrt{n}(\bar{x}-\mu)}{\sigma} < 1.96 \Bigr] = 0.95](images/EXTERN_0005.png)
![{\rm Pr} \bigl[ \bar{x} - 1.96 \cdot\frac{\sigma}{\sqrt{n}} < \mu < \bar{x} + 1.96 \cdot\frac{\sigma}{\sqrt{n}} \Bigr]](images/EXTERN_0006.png)

