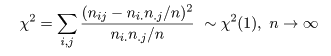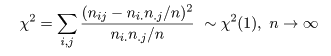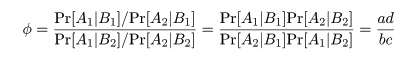2011.10.17
9-2.クロス集計と独立性の検定
n 標本を2つの変数 A,B で分類したとき,2つの変数に関連があるかを調べたい.
変数 A を集団属性(集団1,集団2),変数 B を反応パターン(反応1,反応2)とした
とき,データは以下のようにまとめられる.これをクロス集計と呼ぶ.
2 × 2 分割表データ
| | 反応1 | 反応2 | 計 |
|---|
| 集団1 | n11 |
n12 |
n1・ |
|---|
| 集団2 | n21 |
n22 |
n2・ |
|---|
| 計 | n・1 |
n・2 |
n |
|---|
ここで,nij は,集団 i の標本の中で,反応 j を取った人数(度数)
である.また,ni・ は集団 i の標本の大きさで,
n・j は標本全体(大きさ n)の中で反応 j を取った人数
を表し,それぞれ周辺度数という.
このような表において,集団で反応パターンに違いがなければ,集団 i で反応 j を取る確率は,
集団 i である確率 ni・/n に
集団 j である確率 n・j/n をかけた
ni・n・j/
n2 となることが期待される.これより,
集団 i で反応 j を取る人数(度数)は,
ni・n・j/n
となることが期待される.これを独立性の仮定という.
いま,集団 i の標本の中で,反応 j を取る確率を pij とし,集団 i の周辺確率を pi.,
反応 j の周辺確率を p.j とすると,独立性の仮説は,
帰無仮説,H0: pij = pi.p.j,
対立仮説,H1: pij ≠ pi.p.j,
の検定になる.帰無仮説のもとで,表現は違うが前節とまったく同じ χ2 値が,
と分布するので,独立性の検定を行うことができる.
すなわち,比率の同等性の検定と独立性の検定は,意味が違うが検定のやり方はまったく同じである.
9-3.オッズ比(odds ratio)
変数 A,B 間の関連の強さを測る指標としてオッズ比がある.
たとえば,食中毒事件が起きたとき,
食中毒症状が出たか出なかったか(変数 A)を
出された食材を食べた人と食べなかった人(変数 B)で
分類する.このとき,ある食材に対しての分類は以下のようであったとする.
| | 発症あり(A1) | 発症なし(A2) |
|---|
| 食べた(B1) | a | b |
|---|
| 食べなかった(B2) | c | d |
|---|
食材を食べたときに発症する確率 Pr[A1| B1] の推定値は a/(a + b),
発症しない確率 Pr[A2| B1] の推定値は b/(a + b) である.
これより,その食材を食べたとき食中毒を発症する危険率(オッズ)は,
Pr[A1| B1]/P[A2| B1] = a/b
であり,同様に食べなかったときの発症オッズは,
Pr[A1| B2]/P[A2| B2] = c/d
である.この両者の比,
をオッズ比といい,ある食材を食べたことが食中毒症状発症にどれだけ危険であるかの尺度になる.
危険が同等のときは,オッズ比は 1 となる.なお,どこかのセルデータが 0 であったときは,
セルのすべての値に 0.5 を加えて補正する.
ピアソン χ2 検定は,
帰無仮説 H0:オッズ比 φ = 1
の検定と同等である.
- 例題:食中毒原因食材の χ2 独立性検定とオッズ比
1940 年のNew York 州Oswego の協会の夕食会における胃腸炎異常発生の喫食
調査データによると,出された食材の喫食と食中毒症状で以下の関係があった.これより,
食中毒の原因食材を推定せよ.
| 食品名 | 発症あり | 発症なし |
|---|
| 食べた | 食べない | 食べた | 食べない |
|---|
| ケーキ | 27 | 19 |
13 | 16 |
|---|
| バニラアイス | 43 | 3 |
11 | 18 |
|---|
- 解答
- 表から食材ごとに 2 × 2 分割表つくり,そこから観測度数と期待度数との偏差を出して
ピアソンの χ2 値を計算する.
- ケーキの発症リスクを調べる.
ケーキと食中毒の関係
| | 発症あり | 発症なし |
計 |
|---|
| 食べた | 27 | 13 |
40 |
|---|
| 食べなかった | 19 | 16 |
35 |
|---|
| 計 | 46 | 29 |
75 |
|---|
ピアソンχ2 値の計算
| | 観測度数 | 期待度数 |
偏差の計算 | χ2 値 |
|---|
| 食べて発症 | 27 | 40*46/75 = 24.53 |
(27 - 24.53)2/24.53 | 0.249 |
|---|
| 食べて発症しない | 13 | 40*29/75 = 15.47 |
(13 - 15.47)2/15.47 | 0.394 |
|---|
| 食べないで発症 | 19 | 35*46/75 = 21.47 |
(19 - 21.47)2/21.47 | 0.284 |
|---|
| 食べないで発症しない | 16 | 35*29/75 = 13.53 |
(16 - 13.53)2/13.53 | 0.451 |
|---|
| 計 | 75 | 75 |
| 1.378 |
|---|
- オッズ比 = (27*16)/(13*19) = 1.75
- ケーキの場合,χ2 = 1.37,であり,5 %有意の 3.84 より小さいので,
ケーキの喫食と食中毒発症とは独立であるという帰無仮説は棄却されない.すなわち,ケーキは食中毒
の原因食材ではないと言える.
オッズ比 φ = 1.75 で,ケーキの喫食の食中毒に対するリスクは少し大きい程度である.
- 問題
- バニラアイスの食中毒に対するリスクを分析せよ.
Copyright (C) 2008, Hiroshi Omori. 最終更新:2011年10月17日