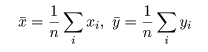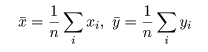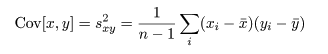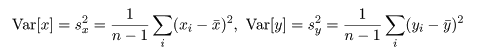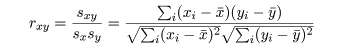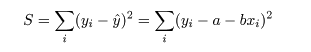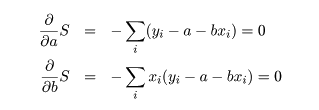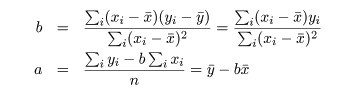統計学の基礎(12.05)

2011.12.05

11．２変量間の関係

11-1．相関

　標本（サンプル）に対し，２つの変数 x，y が測定されているとする．たとえば，x が身長(m)であり，y が体重(kg)である．大きさ n の標本（サンプル）に対し，２つの変数の組のデータが，

（x₁ ，y₁ ），（x₂ ，y₂ ）， …，（x_n ，y_n ）

であったとする．変数間の関連性の強さを測る量として共分散（Covariance），Cov(x ，y ）がある．これは，変数に対する平均を，

として，

と定義される．

　共分散は測定単位により大きさが変わるので，これをおのおのの変数の分散， Var(x)，Var(y)，

で標準化したものが相関係数 r，-1≦r≦1，であり，

と定義される．これは，変数間の線形的関係の強さ，
（x が大きいと y も大きく，x が小さいと y も小さい，）
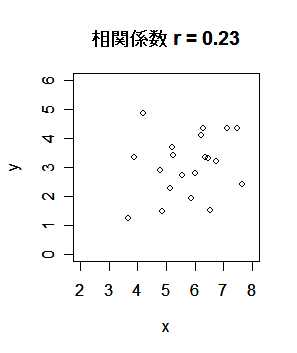
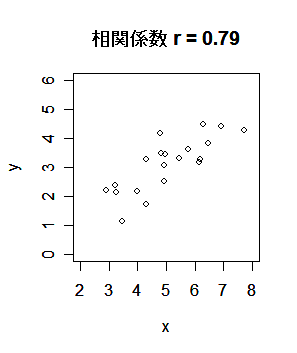
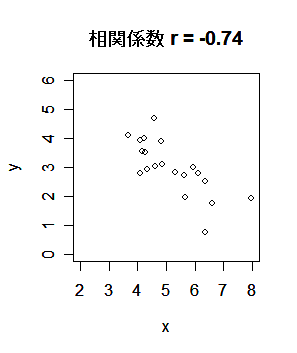
を測る指標で，｜r｜＝1 のときは，変数 x，y は完全な直線関係にあり，r ＝0 のときは，線形的な関係がない．r が 1 に近いときは，正の相関関係があるといい， r が -1 に近いときは，負の相関関係があるという．

データ散布図と相関係数
sokan sokan

sokan sokan

11-2．回帰分析

直線回帰

　２つの変数 x ，y に対し，y の値が x の値の動きにつれて線形的に変化すると仮定される，つまり，

y ＝ a ＋ b x

という関係が成り立っていると考えられる場合である．これを y の x に対する直線回帰といい，a ，b を回帰係数という．また，変数 y を従属変数，目的変数といい，変数 x を独立変数，説明変数という．

最小２乗法

　データに最もよくあてはまる直線回帰式を得るには，データ点（x_i ，y_i ），と回帰による推定点，（x_i ，y^_i ）， y^_i ＝ a ＋ b x_i ，の間の距離の２乗和 S が最小になるような回帰係数 a ，b を求める．つまり，

を最小化する a ，b を求める問題に帰着する．これを最小２乗法という．

　これは，S を a ，b で偏微分して 0 とおくことによって得られる．つまり，

の連立方程式を a ，b で解けばよい．これより，

が得られる．

例題

　下の表はアメリカのあるビジネススクール（MBA）での女子学生の入試得点と初年度成績である．

入試得点（x） 680 500 600 420 480 630 550 590 610 500 640 570 610

初年度成績（y） 332 265 309 253 276 326 299 310 324 327 334 301 336

入試得点（x）	680	500	600	420	480	630	550	590	610	500	640	570	610
初年度成績（y）	332	265	309	253	276	326	299	310	324	327	334	301	336

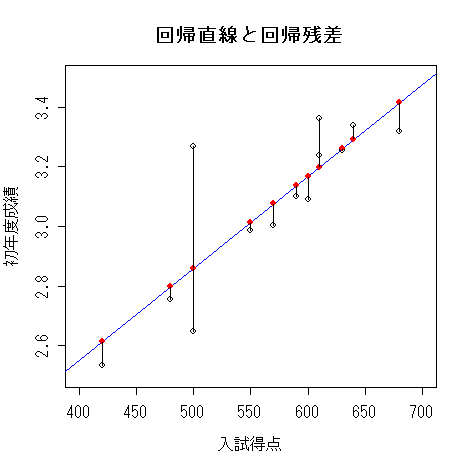
　入試得点を説明変数（x），初年度成績を目的変数（従属変数）（y）として回帰式を求めてみよう．