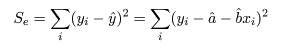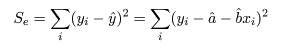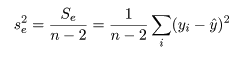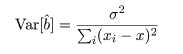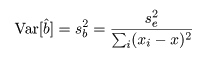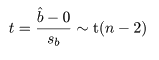統計学の基礎(12.12)

　推定された直線回帰式がどの程度現実のデータに適合しているかを調べるために，回帰式が従う統計モデルを考える．標本の格データ点，（x_i ，y_i ），が，

y_i ＝ a ＋ b x_i ＋ e_i ， e_i ～ N( 0，σ² )

であると仮定する．e_i は誤差（error），あるいは，残差（residual）で，直線回帰式では説明がつかない部分を表し，これが互いに独立に平均 0，分散 σ² の正規分布に従うと仮定する．誤差の大きさが大きいときは，直線回帰式ではデータが説明できないと考える．

　回帰で説明がつかない残差平方和 S_e は，

で求められる．これの自由度は n－2 であるので（２つの回帰係数分の自由度を除く），回帰の残差（誤差）分散は，

で求められる．

　一般に，Var(y_i ) ＝ σ² であるとき，その定数倍の分散は，

Var(ay_i ) ＝ a²σ²， Var(Σ_ia_i y_i ) ＝ Σ_ia_i ² σ²

であり，従属変数 y のデータ y_i は，

y_i ～ N( a ＋ b x_i ，σ² )

と分布するので，回帰係数 b の分散は，

となる．この分散の平方根を回帰係数 b の標準誤差という．

目的変数 y が説明変数 x との回帰関係にないという帰無仮説，

H₀：b ＝ 0，

を考えてみよう．

回帰係数 b の推定値 b^ の分散は，

と推定できるので，b^ の標準誤差は， s _b と推定される．これより，回帰係数をその標準誤差で割った t 値が，帰無仮説のもとで，

のように，自由度 n－2 の t 分布に従うことを利用して回帰係数の検定が行える．すなわち，自由度 n－2 の t 分布の 97.5％点を t₀ とすると，

|t | ＞ t₀ → 帰無仮説を有意水準 5 ％で棄却（回帰関係が有意に認められる）

|t | ≦ t₀ → 帰無仮説を棄却しない（回帰関係が認められない）

と定式化できる．