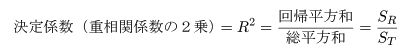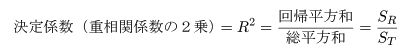2011.12.19
回帰係数の信頼区間
回帰係数の標準誤差 s b を用いて,
回帰係数 b の信頼区間がつくれる.すなわち,
自由度 n−2 の t 分布の 97.5%点を t0 とすると,
回帰係数 b の 95%信頼区間の幅 d は,d = t0
s b となるので, 95%信頼区間は,
b^ − t0
s b < b <
b^ + t0
s b
となる.
例題
女子学生の入試得点(x)と初年度成績(y)のデータにおいて求めた回帰式
y = a + b x
において,x と y は回帰関係に無いという帰無仮説
H0 : b = 0
の検定を行え,また,回帰係数 b の95%信頼区間を求めよ.
平方和分解と分散分析
回帰式により,
従属変数 y のデータ yi は,
yi = y^i
+ (yi −
y^i ) =
回帰値 + 残差
のように分解される.この分解に対応して従属変数データの総平方和 ST は,
ST = Σi
(y i − y- )
2 =
Σi
(y^i − y- )
2 +
Σi
(y i −
y^i )
2 = SR + Se
総平方和 = 回帰平方和 + 残差平方和
のように分解される.これを平方和の分解という.この分解に対応して自由度は,
n−1 = 1 + n−2
と分解される.
データが直線回帰式でよく説明できるのは,回帰平方和が大きく,残差平方和
が小さい場合である.総平方和のうち回帰平方和で説明される割合を決定係数,もしくは
重相関係数の2乗といい,
で定義される.なお,重相関係数 R とは,データ y i
と回帰推定値 y^i との間の相関係数である.これより,
以下の分散分析表ができる.
回帰分析の分散分析表
| 変動因 | 平方和 | 自由度 | 平均平方 | F 値 |
| 回帰 | SR | 1 |
SR |
F = SR/se2 |
| 残差 | Se | n−2 |
se2 = Se/n−2 |
|
| 全体 | ST | n−1 |
|
|
分散分析による F 検定
従属変数 y が説明変数 x の回帰関係にないという
帰無仮説,
H0:b = 0,
を考える.帰無仮説のもとでは,回帰平均平方 SR と残差分散 se2
がともに誤差 σ2 の不偏推定量になるので,
その比 F 値が,
F = SR/se2
〜 F(1,n−2),
という F 分布に従うことを利用して検定ができる.すなわち,分子,分母
自由度が 1,n−2 である F 分布 F(1,n−2)の95%点を F0 とすると,
F > F0 → 帰無仮説を有意水準 5 %で棄却(回帰関係が有意に認められる)
F ≦ F0 → 帰無仮説を棄却しない(回帰関係が認められない)
と定式化できる.
F 分布
U が自由度 m の χ2 分布に従い
(U 〜 χ2(m)),
また,V 〜 χ2(n)と
分布し,U と V が互いに独立であるとする.このとき,
2つの χ2 分布する確率変数をそのおのおのの自由度
で割った量の比を F 値といい,
F = (U/m)/(V/n)
は自由度 m,n の F 分布に従い,F 〜 F(m, n) と表記する.
m を分子の自由度,n を分母の自由度という.
ところで,回帰係数の推定値 b^ をその
標準誤差 sb で割った t 値は,
回帰関係がないという帰無仮説 H0,
H0:b=0
のもとで自由度 n − 2 の t 分布に従う,すなわち,
t = b^/sb 〜 t(n−2)
となる.この関係において,
t 2 〜 F(1, n−2)
が成り立つ.つまり,t 分布をより一般化したのが F 分布である.
この F 分布を用いた F 検定が,回帰分析や分散分析でよく用いられる.
例題
女子学生の入試得点(x)と初年度成績(y)のデータにおいて求めた回帰式
y = a + b x
において,分散分析表を作り,回帰式に意味が無いという帰無仮説の検定を行え.また,この回帰関係の
決定係数(重相関係数の2乗:R2)を求めよ.
ただし,自由度 1,11 の F 分布の 95 %点は 4.84,99%点は 9.65 である.
Copyright (C) 2008, Hiroshi Omori. 最終更新:2011年12月19日