2011.4.25
東京国際大学
統計学の基礎
東京大学大学院農学生命科学研究科 大森宏
講義プリントサイト:http://lbm.ab.a.u-tokyo.ac.jp/~omori/kokusai11/
携帯解答サイト: http://lbm.ab.a.u-tokyo.ac.jp/~omori/k/
QRコード
1. 統計的データはどのように用いられているか
1-1.データの使用例
世論調査,視聴率,政党支持率,株価,売上高,販売シェア…
など多岐にわたる.
主張や意見に説得力をもたせるため.
漢字検定データ例(文献4)
日本漢字能力検定協会が発表したデータに対し,共同通信(2005/08/25)が以下の記事を配信した.
-
大学生は漢字が苦手.高卒程度問題,正答率4割
-
高校卒業程度とされる漢字検定2級の問題で,大学1年生の正答率が39.8%しかなかった
ことが24日,日本漢字能力検定協会(京都市下京区)による初めての調査でわかった.
大学生が高校教育課程の漢字を習得しないまま卒業・進学している実態が浮かんだ.
調査は今年4−5月,首都圏と関西圏,東海地区から無作為に抽出した中学,高校,大学の
新入生と上場企業の新入社員計8356人を対象に実施.漢字検定で過去に出題した問題を使い,
同音・同訓異字,熟語の読み書きなどを記述させた.
大学1年生には,「閑古鳥」「吟味」「醜聞」の読みや「魚のクサミ」「マイゾウ文化財」
「門前のコゾウ」の漢字を書かせる問題などが出題された.
小学校卒業程度(同5級)での中学1年生の正答率は78.5%,中学卒業程度の問題(同3級)での
高校1年生の正答率は59.0%で,同協会は「高学年になるほど漢字学習がおろそか,学習の積み残し
が増えている」と指摘,新入社員も大学生と同じ2級で60.7%の正答率にとどまった.
1-2.データの視覚化
1.表による整理
文章中の数字は,表にまとめるとより見やすくなる(と思う).
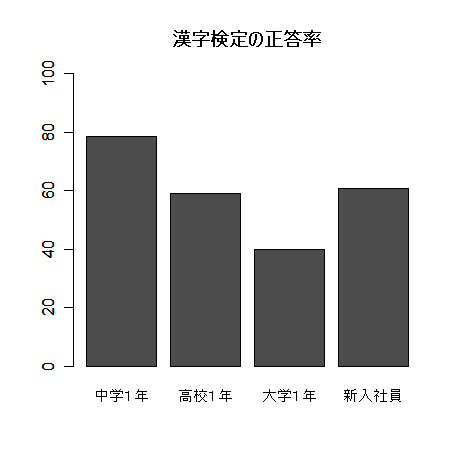
漢字検定の正答率
| 調査対象 | 正答率(%) |
| 中学1年生 | 78.5 |
| 高校1年生 | 59.0 |
| 大学1年生 | 39.8 |
| 新入社員 | 60.7 |
2.グラフ表示
表よりグラフの方がより見やすい(と思う).
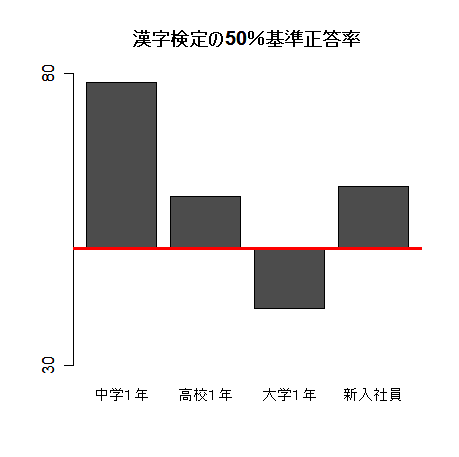
3.グラフ強調表示
基準線を変えると,より主張(大学生は漢字が苦手)が強調される(と思う).
設問
- 問1:共同通信社は「大学生は漢字が苦手」と主張したが,それに対する考えを以下から選び,
選択肢回答テスト第1問に携帯から送信せよ.
- 1.共同通信社の主張に全面的に同意する.
- 2.共同通信社の主張にそういわれればそうだなと感じた.
- 3.共同通信社の主張には納得いかない点がある.
- 4.共同通信社の主張にはまったく納得がいかない.
-
- 問2.問1の回答の理由を掲示板に投稿せよ.
1-3.なにを比較しているかの吟味
1.母集団
調査対象がどのような集団を想定しているのか(これを母集団という)を考える.
漢字検定の例では,標本抽出を「首都圏と関西圏,東海地区」から行っているので,日本の大都市圏の住人である.
また,「無作為」に対象を選らんでいるので,偏り(バイアス)はない.
たとえば,ネット調査の場合,ネットに対する興味などの偏りが生じる恐れがある.
各比較対象ごとに詳しくみると,
- 中学1年:義務教育なので,同世代を完全に代表している.
- 高校1年:進学率98%なので,同世代をほぼ完全に代表している.
- 大学1年:進学率50%なので,同世代の一部を代表するのみであるが,進学するからには漢字などの
学業能力が比較的高いと想定される.
- 上場企業新入社員:同世代の極一部のみを代表するのみ.上場企業で採用されたことにより,漢字などの
学業能力はかなり高いと想定される.
2.比較内容
2つ以上の集団を比較する場合,それぞれの集団に同じ処理をほどこすのが普通である.そうしないと,
処理の効果の集団での違いがわからず,何を比較したのかがわからなくなる.
漢字検定試験では,大学1年生と新入社員は,漢字検定2級(高校卒業程度)で試験を行ったが,
高校1年生は漢字検定3級(中学卒業程度),中学1年生は漢字検定5級(小学校卒業程度)を
行っており,集団全体は同じ処理をほどこしていない.
以上をまとめると,
漢字検定の正答率
| 調査対象 | 対象属性 | 正答率(%) | 試験内容 |
| 中学1年生 | 大都市圏居住同世代を完全に代表 |
78.5 | 漢字検定5級(小学校卒業程度) |
| 高校1年生 | 同世代をほぼ代表 |
59.0 | 漢字検定3級(中学卒業程度) |
| 大学1年生 | 同世代の半数を代表(漢字能力が比較的高い) |
39.8 | 漢字検定2級(高校卒業程度) |
| 新入社員 | 同世代の極一部のみ代表(漢字能力が高い) |
60.7 | 漢字検定2級(高校卒業程度) |
2. 質的データと量的データ
統計学で取り扱う値は,変数という考え方で分類できる.
2-1. 変数
質的変数
- 順序なしカテゴリー:
性別(男女),職業(公務員,会社員,学生,主婦,無職など)
- 順位的変数:
成績(優,良,可,不可),嗜好(好き,嫌い),選考(はい,どちらでもない,いいえ)
量的変数
- 離散的(自然数):
世帯数,交通事故数(場合の数がそれほど多くない)
- 連続的(実数):
長さ,身長,重さ,売り上げ(連続的とみなせる)
2-2. 測定
対象に何らかの標識を与える操作(尺度化).データを取ること.
- 名義尺度:
対象をカテゴリーに分ける(順序なしの質的変数に割り付けること)
- 順序尺度:
対象を順序つきのカテゴリー(順位変数)に分けること.
- 間隔尺度:
年次,温度(セ氏)など.数値間の差(引き算)に意味がある.
- 比例尺度:
0が存在する(意味がある).質量(重さ),長さ,価格,絶対温度.
引き算ばかりでなく,比例(割り算)にも意味がある.
参考文献
- 心理・教育のための統計法(第 2 版),山内光哉,1998,サイエンス社
- 工学のためのデータサイエンス入門−フリーな統計環境Rを用いたデータ解析−,間瀬茂ら,2004,
数理工学社
- 実践生物統計学−分子から生態まで−(第 1 章,第 2 章),
東京大学生物測定学研究室編(大森宏ら),
2004,朝倉書店
- R で学ぶデータマインニング I −データ解析の視点から−,熊谷悦生・船尾暢男,2007,九天社
- R で学ぶデータマインニング II −シミュレーションの視点から−,熊谷悦生・船尾暢男,2007,九天社
Copyright (C) 2008, Hiroshi Omori. 最終更新:2011年 4月24日