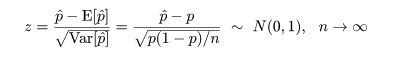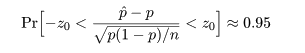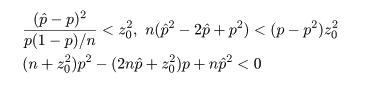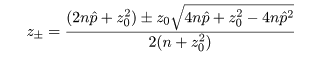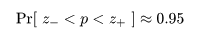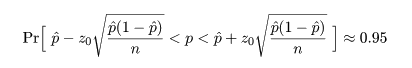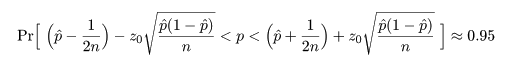統計学の基礎(9.26)

2011.9.26

東京国際大学

統計学の基礎（後期）

東京大学大学院農学生命科学研究科　大森宏

講義プリントサイト：http://lbm.ab.a.u-tokyo.ac.jp/~omori/kokusai11/koki.html

夏休みの宿題

集合知による景観解析

9月22日時点で，119名の提出がありました．ご協力ありがとうございました．現在、整理中です．

７．比率に関する統計的推論

　製品の不良率，政権への支持率，テレビ視聴率などの比率に関する統計的推論を取り扱う．比率に関して基礎となる二項分布を学び，それを正規分布に近似して統計的推論を行うことを学ぶ．
たとえば，今年の大河ドラマ江は初回視聴率23.2％だったが，視聴率は標本調査なので誤差がつきまとう．この標本誤差の取り扱い方を学び，真の視聴率の 95％信頼区間を求める手法を学ぶ．

7-1．二項分布

　成功確率 p の事象を n 回試行したときの成功回数 r の分布
r ～ B(n, p) と書く．
　成功回数が r となる確率 Pr[r ] は，n 回の試行で r 回成功する場合の数が _nC_r 通りで，r 回成功し n－r 回失敗するので，

Pr[r ] ＝ _nC_r p^r (1－p)^n－r

となる．

例題

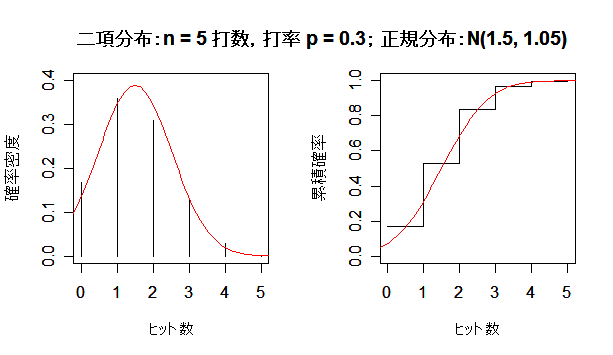
A 選手は 3 割バッターである．ある試合で 5 回打席に立ったときときのヒット数の分布を求める．
この場合，p＝0.3，n＝5である．

5打数ノーヒットの確率：Pr[0]
ヒットが出ない確率は，1－0.3＝0.7なので，求める確率は，Pr[0] ＝ 0.7⁵ ＝ 0.16807
5打数1安打の確率：Pr[1]＝₅C₁ p(1－p)⁴ ＝5×0.3×0.7⁴＝1.5×0.2401＝0.36015
5打数2安打の確率：Pr[2]
解答：Pr[2]＝₅C₂ p²(1－p)³ ＝ (5*4)/(2*1)×0.3²×0.7³＝ 0.3087
5打数3安打の確率：Pr[3]＝₅C₃ p³(1－p)² ＝(5*4*3)/(3*2*1)×0.3³×0.7²＝10×0.027×0.49＝0.1323
5打数4安打の確率：Pr[4]＝₅C₄ p⁴(1－p) ＝5×0.3⁴×0.7＝3.5×0.0081＝0.02835
5打数5安打の確率：Pr[5]＝p⁵＝0.3⁵＝0.00243

　これより，ヒット数の分布は以下の表のように書ける．

ヒット数 0 1 2 3 4 5

確　率 0.16807 0.36015 0.3087 0.1323 0.02835 0.00243

ヒット数	0	1	2	3	4	5
確　率	0.16807	0.36015	0.3087	0.1323	0.02835	0.00243

一般に，二項分布などの離散確率分布は，取ることができる値 x_i ごとに，その値をとる確率 p_i，Σ p_i ＝ 1，が定義されている．つまり，

値 x₁ x₂ … x_n

確　率 p₁ p₂ … p_n

値	x₁	x₂	…	x_n
確　率	p₁	p₂	…	p_n

の形で表現される．このとき，確率分布の平均と分散は，

平均： x^- = x₁p₁ + x₂p₂ + … + x_np_n = Σ_ix_ip_i
分散: s² = (x₁ - x^-)²p₁ + (x₁ - x^-)²p₁ + … + (x_n - x^-)²p_n = Σ_i(x_i - x^-)²p_i

と定義される．

　これより，ヒット数の平均と分散は，

平均： x^- = 0*0.16807 ＋ 1*0.36015 ＋ 2*0.3087 ＋ 3*0.1323 ＋ 4*0.02805 ＋ 5*0.00243 = 1.5
分散： s² = (0－1.5)²*0.16807＋(1－1.5)²*0.36015 ＋(2－1.5)²*0.3087
＋ (3－1.5)²*0.1323＋(4－1.5)²*0.02805 ＋(5－1.5)²*0.00243 = 1.05

と計算される．実は，成功確率 p の事象を n 回行ったときの二項分布 B(n，p) の平均と分散は，

平均： x^- = np = 5*0.3 = 1.5， 分散： s² = np(1 - p) = 5*0.3*0.7 = 1.05

となることがわかる．

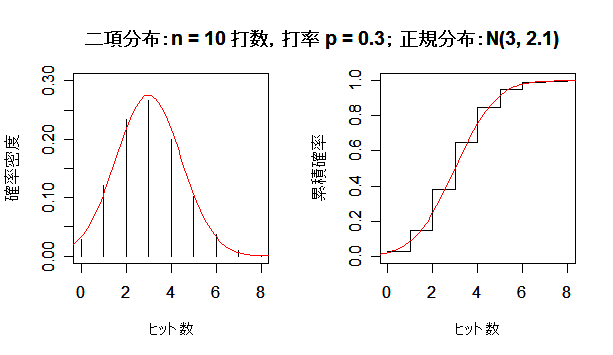
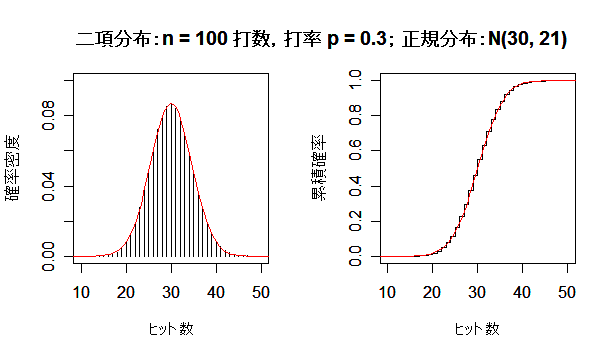
二項分布が正規分布に近づく様子

　成功確率 p の二項分布は，試行回数 n を増やしていくと，平均 np，分散 np(1 - p) の正規分布に近づく．左図が確率分布（密度）で，右図が累積分布である．

7-2．成功確率（比率）の信頼区間

　成功確率 p のベルヌイ試行を n 回行ったとき x 回成功したとすると，成功確率は， p^{^} = x/n，と推定される．
　成功回数 x は二項分布し，その平均は E[x ] = np，分散は Var[x ] = np(1 - p)，であるので，成功確率推定量 p^{^} の平均は E[p^{^} ] = E[x/n] = p，分散は Var[p^{^} ] = Var[x/n] = Var[x ]/n² = p(1 - p)/n，となる．これより，

と漸近的に分布するので，標準正規分布の 97.5％点の z₀ = 1.96 を用いると，近似的に

という不等式が成り立つ．これを整理すると，

という p の２次不等式を解くことに帰着する．いま，p の２次方程式の根を

とすると，この根を用い，p の 95％信頼区間は近似的に

となる．

　試行回数 n が十分大きいと思われるときは，さらに近似を加え，成功確率推定量 p^{^} の分散において，真の成功確率 p の代わりにその推定量 p^{^} に置き換えて，Var[p^{^} ] = p^{^}(1 - p^{^})/n，とみなすと， p の近似的な 95％信頼区間は，

と簡略化される．
　簡略化された信頼区間で連続性の補正を入れるには，

として，信頼区間の幅を拡げる．

　ところで，正規近似による信頼区間の構成では，場合により信頼区間が負になったり 1 を超えることがあるが，このときは，0 と 1 で切り詰める．

例題（テレビ視聴率）: テレビ視聴率は，視聴率の高い番組ほど多くの視聴者が見ているので，広告宣伝の効果が高く影響力が強いと考えられている．このため，視聴率の高さが広告宣伝費用に反映されるので，テレビ会社は高い視聴率を得ようとして番組を製作している．
ある調査会社のデータによると，関東地区では 600 世帯を対象にしているようである． NHK 大河ドラマの関東地区世帯視聴率は26.2％であった．真の世帯視聴率の 95 ％信頼区間を求めよ．
解答：: p の分散推定値は s² = p^{^}(1 - p^{^})/n = 0.262*(1 - 0.262)/600 = 0.262*0.738/600 = 0.00032226
p の標準偏差の推定値（標準誤差）は s = √0.00032226 = 0.01795
95 ％信頼区間の幅は d = z₀s = 1.96*0.01795 = 0.035
下限は，p^{^} - d = 0.262 - 0.035 = 0.227，上限は，p^{^} + d = 0.262 + 0.035 = 0.297
よって，0.227 < p < 0.297 である．