f1 <- function(x){
exp(x)-2
}
#関数のグラフ
x <- seq(-1, 2, by=0.01)
plot(x, f1(x), type="l")
# これでもよい
curve(f1(x), -1,2)
#水平線と垂直線
abline(h=0)
abline(v=0)
#グラフタイトル
title(main="f(x) = exp(x) - 2 のグラフ")
# 0 < x < 1 で根を探す
uniroot(f1, c(0,1))
統計解析ソフトRを用いて,統計解析が自在に行えるスキルを身に着ける.また,解析的証明より, シミュレーションによる数値的な証明(厳密ではないが直感的に理解しやすい)を行い,統計学の 視覚的で直感的な理解をめざす.
| x <- c(2, 3, 5) | #ベクトルの定義 | |
| y <- c(10, 14, -7) | ||
| a <- matrix(1:9, nrow=3) | #行列の定義 | |
| b <- x %*% t(x) | #行列の積 | |
| z <- c(6, -5, 2) | ||
| a1 <- cbind(x,y,z) | #列ベクトル−>行列生成 | |
| solve(a1) | #逆行列 | |
| eigen(a1) | #固有値 | |
| x <- 1:10 | #連続した自然数 | |
| y <- c(3,7,8,6,9,10,6,5,10,7) | ||
| plot(x, y) | #散布図 | |
| plot(x, y, type="l") | #直線でつなぐ | |
| x <-seq(-20, 20, by=0.1) | #等間隔点列 | |
| y <- x^2 | #関数定義 | |
| y <- 3*x^3 - 2*x^2 + 6*x + 5 | ||
| y <- -2*cos(x)+4*sin(x) | ||
| plot(x, y, type="l") | #関数のグラフ | |
| plot(x, y, type="l", xlim=c(-20,20), ylim=c(-20,20)) | #表示部分の指定 | |
|
# 関数の作成 f1 <- function(x){ exp(x)-2 } #関数のグラフ x <- seq(-1, 2, by=0.01) plot(x, f1(x), type="l") # これでもよい curve(f1(x), -1,2) #水平線と垂直線 abline(h=0) abline(v=0) #グラフタイトル title(main="f(x) = exp(x) - 2 のグラフ") # 0 < x < 1 で根を探す uniroot(f1, c(0,1)) |
|
|
|
|
| ||||||||||||||||||||||||
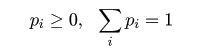
| (1. 1) |
| 変数 X | x1 | x2 | x3 | x4 | x5 |
|---|---|---|---|---|---|
| 確率 P | p1 | p2 | p3 | p4 | p5 |
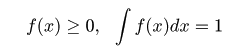
| (1. 2) |
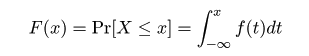
| (1. 3) |
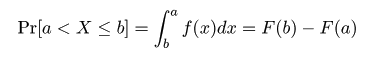
| (1. 4) |
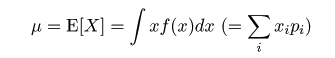
| (2. 1) |
|
|
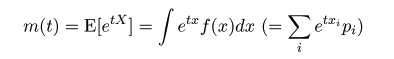
| (2. 3) |
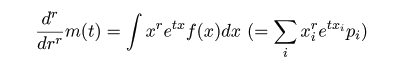
|
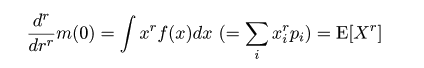
| (2. 4) |
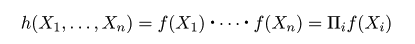
| (3. 2) |
平均が μ である分布をもつ母集団から大きさ n の無作為標本 X1,…,Xn を抽出したときに,
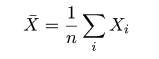
| (3. 3) |
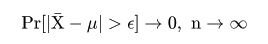
| (3. 4) |
| 変数 X | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 確率 P | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
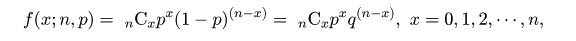
| (4. 1) |
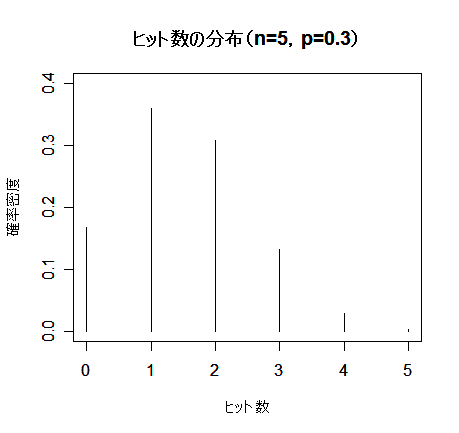
| n <- 5 | #試行回数 |
| x <- 0:n | #回数 |
| p <- 0.3 | #成功確率 |
| hit <- dbinom(x, size=n, prob=0.3) | #二項確率 |
| plot(x, hit, type="h", ylim=c(0,0.4), xlim=c(0,n), cex.lab=0.8, xlab="ヒット数", ylab="確率密度") | |
| title(main="ヒット数の分布(n=5,p=0.3)") | #タイトル |
| sum(x*hit) | #平均(np = 1.5) |
| sum(hit*(x - n*p)^2) | #分散(np(1 - p) = 1.05) |
| 5,6の個数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| 出た回数 | 185 | 1149 | 3265 | 5475 | 6114 | 5194 | 3067 |
| 5,6の個数 | 7 | 8 | 9 | 10 | 11 | 12 | 合計 |
| 出た回数 | 1331 | 403 | 105 | 18 | 0 | 0 | 26306 |
| モデル | 平均 | 分散 |
|---|---|---|
| データ | 4.052 | 2.696 |
| 2項分布(p=0.338) | 4.052 | 2.685 |
| 2項分布(p=0.333) | 4 | 2.667 |
| x <- 0:12 | #個数 |
| dice <- c(185,1149,3265,5475,6114,5194,3067,1331,403,105,18,0,0) | #回数データ |
| sum(dice) | #試行回数 |
| pdice <- dice/sum(dice) | #回数の確率 |
| m <- sum(x*pdice) | #平均 |
| p <- m/12 | #5,6の出る確率 |
| s2 <- sum(pdice*(x-m)^2) | #分散 |
| v <- 12*p*(1-p) | #二項分布のもとでの分散 |
| h1 <- dbinom(x, 12, 1/3) | #正しいサイコロのもとでの二項確率分布 |
| h2 <- dbinom(x, 12, p) | #推定確率からの二項確率分布 |
| dicedis <- rbind(pdice,h2,h1) | #行ベクトル−>行列 |
| colnames(dicedis) <- as.character(0:12) | #列の名前 |
| barplot(dicedis, beside=TRUE, cex.axis=0.8, cex.lab=1.0, xlab="5,6の個数", ylab="確率", legend=c("データ","p=0.338", "p=0.333")) | |
| title(main="Weldon のサイコロ実験の分布") | #グラフタイトル |
| 女児数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| 度数 | 7 | 45 | 181 | 478 | 829 | 1112 | 1343 |
| 女児数 | 7 | 8 | 9 | 10 | 11 | 12 | 合計 |
| 度数 | 1033 | 670 | 286 | 104 | 24 | 3 | 6155 |
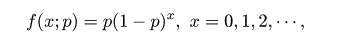
| (4. 2) |
下の負の二項分布で n = 1 とおけば,
m(t) = p/(1 - qet),q = 1 - p
E[X ] = q/p = (1 - p)/p,Var[X ] = q/p2 = (1 - p)/p2
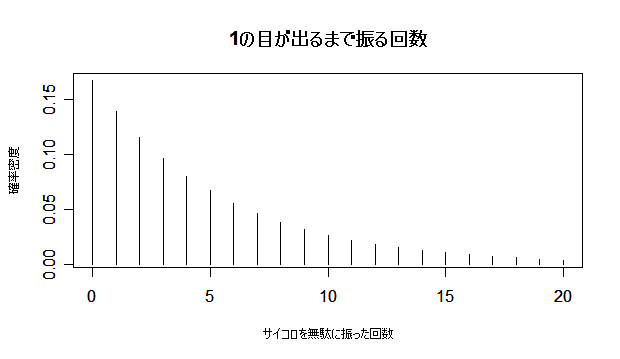
| x <- 0:100 | #本当は無限大まで必要(永遠に1が出ない) |
| p <- 1/6 | #成功確率 |
| y <- dgeom(x, p) | #幾何分布の確率密度) |
| # x は 0 から 20 まで表示 | |
| plot(x, y, type="h", cex.lab=0.8, xlim=c(0,20), xlab="サイコロを無駄に振った回数", ylab="確率密度") | |
| title(main="1 の目が出るまで振る回数の分布") | #タイトル |
| sum(x*y) | #平均((1 - p)/p = (5/6)/(1/6) = 5) |
| sum(y*(x - (1-p)/p)^2) | #分散((1 - p)/p2 = (5/6)/(1/36) = 30) |
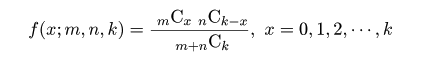
| (4. 3) |
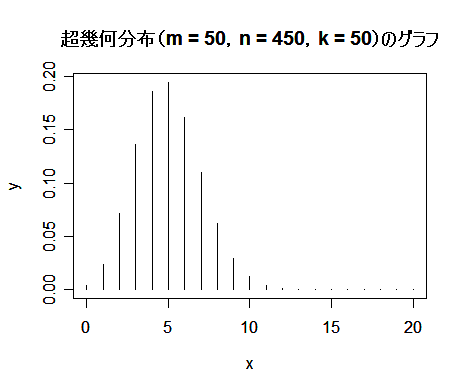
| x <- 0:20 | # 抽出された白石の個数 |
| m <- 50 | # 白石の個数 |
| n <- 450 | # 黒石の個数 |
| k <- 50 | # 抽出回数 |
| y <- dhyper(x, m, n, k) | # 超幾何分布確率分布 |
| plot(x,y,type="h") | # |
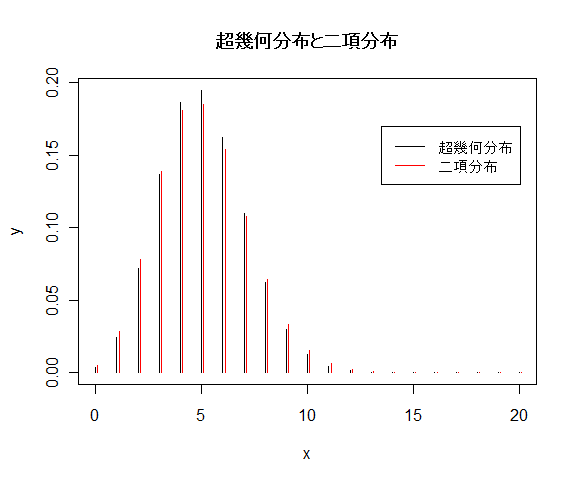
| p <- m/(m+n) | # 白石が選ばれる確率 |
| yd <- dbinom(x, k, p) | # 二項確率 |
| x1 <- x+0.1 | # 0.1 ずらして表示 |
| points(x1, yd, type="h", col="red") | # 二項確率のグラフ |
| title(main="超幾何分布と二項分布") | # |
| legend(locator(1),c("超幾何分布","二項分布"), lty=1, col=c("black", "red")) | |
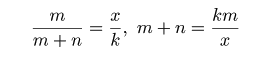
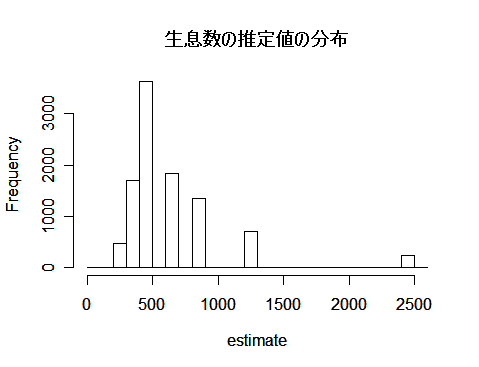
| m <- 50 | # 標識をつけた数 |
| n <- 450 | # 標識をつけられていない数 |
| k <- 50 | # 再捕獲数 |
| estimate <- NULL | # 個体数推定値の定義 |
| for (i in 1:10000) { | # 10000回のシミュレーション |
| x <- rhyper(1, m, n, k) | # 超幾何分布に従う乱数1つ抽出 |
| estimate <- c(estimate, k * m / x) | # 個体数推定値列ベクトル |
| } | # |
| hist(estimate, breaks=seq(0, 2600, by=100), main="") | #推定値のヒストグラム |
| title(main="生息数の推定値の分布") | #タイトル |
| table(estimate) | #推定値の階級分け |
| ord <- order(estimate) | #推定値の順位 |
| estimate[ord[500]] | #小さい方から500番目(5%点) |
| estimate[ord[1000]] | #小さい方から1000番目(10%点) |
| median(estimate) | #メディアン(中央値) |
| estimate[ord[9000]] | #小さい方から9000番目(90%点) |
| estimate[ord[9500]] | #小さい方から9500番目(95%点) |
課題:上の例では捕獲(m = 50),再捕獲(k = 50)合わせて100頭を捕獲している. 捕獲数を半分にした場合の生息数の推定精度はどうなるか.
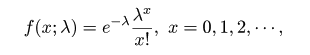
| (4. 4) |
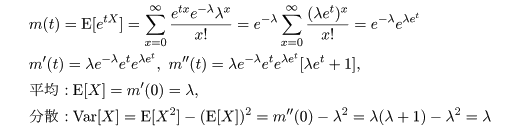
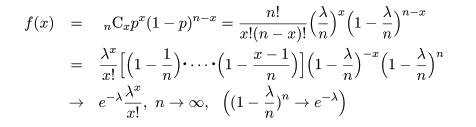
となり,n の極限でこの二項分布は平均 λ のポアソン分布に従うことがわかる.
| x <- 0:8 | #グラフのx軸の範囲 |
| lam <- 2 | #λの定義 |
| yp <- dpois(x,lam) | #ポアソン分布の確率密度 |
| y1 <- dbinom(x, 5, 0.4) | #二項分布(n = 5,p = 0.4)の確率密度 |
| y2 <- dbinom(x, 10, 0.2) | #二項分布(n = 10,p = 0.2)の確率密度 |
| y3 <- dbinom(x, 20, 1/10) | #二項分布(n = 20,p = 0.1)の確率密度 |
| y4 <- dbinom(x, 40, 1/20) | #二項分布(n = 40,p = 0.05)の確率密度 |
| plot(x, y1, type="b", ylab="確率") | #二項分布(n = 5,p = 0.4)のプロット(黒) |
| points(x, y2, type="b", col="green") | #二項分布(n = 10,p = 0.2)のプロット(赤) |
| points(x, y3, type="b", col="blue") | #二項分布(n = 20,p = 0.1)のプロット(青) |
| points(x, y4, type="b", col="purple") | #二項分布(n = 40,p = 0.05)のプロット(紫) |
| points(x, yp, type="b", col="red") | #ポアソン分布のプロット(赤) |
| title(main="二項分布(np = 2)がポアソン分布に近づく様子") | |
| # 凡例の記述(locator(1)は,凡例の記述場所をクリックで指定) | |
| legend(locator(1), c("p=0.4", "p=0.2", "p=0.1", "p=0.05", "ポアソン"), | |
| lty=1, col=c("black", "green", "blue", "purple", "red")) | |
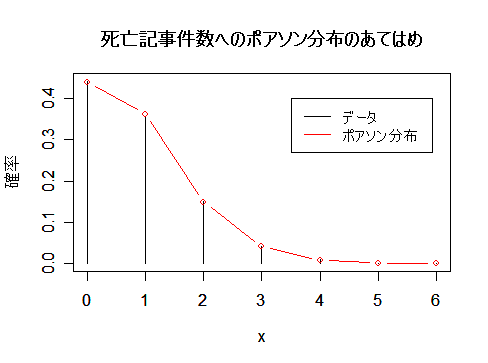
| 死亡記事件数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 以上 |
|---|---|---|---|---|---|---|---|
| 日数 | 484 | 391 | 164 | 45 | 11 | 1 | 0 |
死亡記事件数データの平均は0.8239,分散は0.8294,であった.このデータがポアソン分布に従っている
と考える.ポアソン分布の平均は λ なので,λ = 0.8239 のポアソン分布にあてはめてみたところ,非常によく
一致していた.
また,ポアソン分布は,平均と分散が等しいという特徴がある.データの平均と分散の値が
近いことから,データはポアソン分布によく適合していることを示している.
 |
|
| x <- 0:6 | #グラフのx軸の範囲 |
| y <- c(484, 391, 164, 45, 11, 1, 0) | #死亡記事件数データ |
| s <- sum(y) | #データ総数 |
| m <- sum(x*y/s) | #データ分布の平均 |
| v <- sum((x-m)^2*y/s) | #データ分布の分散 |
| yp <- dpois(x, m) | #平均 m のポアソン分布確率密度 |
| plot(x, y/s, type="h", ylab="確率") | #データの棒グラフ表示 |
| points(x, yp, type="b", col="red") | #ポアソン分布の重ねがき(赤) |
| title(main="死亡記事件数へのポアソン分布のあてはめ") | |
| legend(3.5, 0.4, c("データ", "ポアソン分布"), lty=1, col=c("black","red")) | |
7 日間で売れる商品の個数は,平均 2×7 = 14 のポアソン分布に従うと考えられる.ポアソン分布 の95%(分位)点を求めればよい.これより,必要な在庫は20個とわかる.
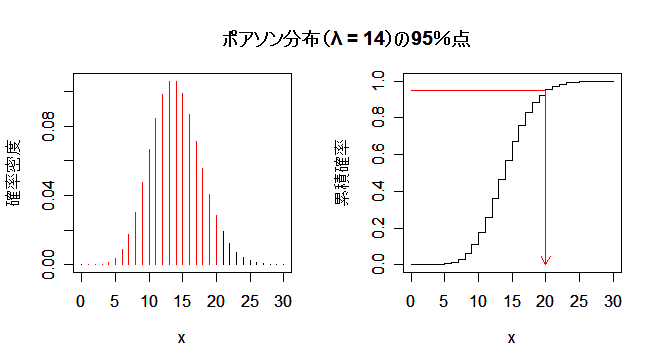
| m <- 14 | # ポアソン分布のパラメータ(平均) |
| x <- 0:30 | # グラフのx軸の範囲 |
| yp <- dpois(x, m) | # ポアソン分布確率密度 |
| cyp <- ppois(x,m) | # ポアソン分布累積確率 |
| stok <- qpois(0.95, m) | # 95%(分位)点 |
| stok | # 答えの表示 |
| op <- par(mfrow = c(1, 2)) | # 横に2つのグラフを並べる |
| plot(x, yp, type="h", ylab="確率密度") | # 確率密度グラフ |
| points(x[2:21],yp[2:21], type="h", col="red") | # x = 20 まで赤色表示 |
| plot(x,cyp,type="s", ylab="累積確率") | # 累積確率グラフ |
| arrows(stok,0.95,stok,0, length=0.1, col="red") | # 赤矢印 |
| segments(0,0.95, stok,0.95, col="red") | # |
| par(op) | # グラフ表示もとに戻す |
| title(main="ポアソン分布(λ = 14)の95%点") | # グラフタイトル |
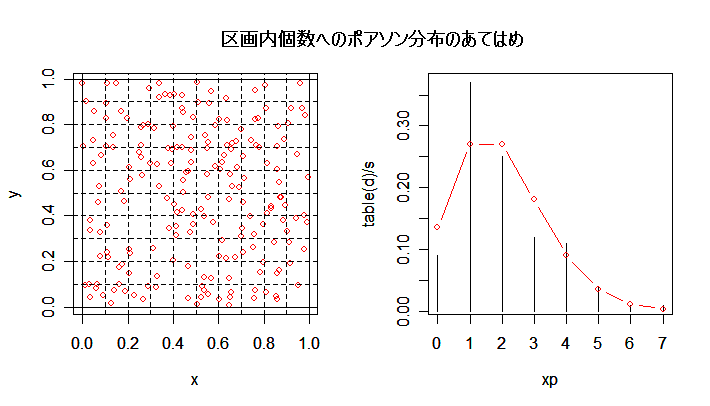
| n <- 200 | # 個体数 |
| m <- 10 | # メッシュ(m2 個) |
| x <- runif(n) | # 一様乱数n個 |
| y <- runif(n) | # 一様乱数n個 |
| # | # |
| count <- NULL | # count の定義 |
| for(i in 1:m){ | # m 回の繰り返し |
| n1 <- (1:n)[x < (i-1)/m] | # (i-1)/m 以下の乱数である番号 |
| n2 <- (1:n)[x < i/m] | # i/m 以下の乱数である番号 |
| nin <- n2[!n2 %in% n1] | # (i-1)/m から i/m の番号 |
| yy <- y[nin] | # 上記 x 座標に対する y 座標 |
| a <- hist(yy, breaks=0:m/m) | # yy を 0 から 1 まで 1/m きざみで区切る |
| count <- c(count, a$counts) | # 区切った領域に入った個体の個数のベクトル |
| } | # 繰り返しここまで |
| mc <- max(count) | # メッシュ内の個数の最大値 |
| xp <- 0:mc | # 個数の定義域 |
| d <- factor(count, levels=xp) | # 個数が 0 の階級も含める |
| table(d) | # メッシュ内個数の区分 |
| s <- sum(table(d)) | # 総個数 |
| m1 <- sum(xp*table(d)/s) | # カウント分布の平均 |
| m2 <- mean(count) | # カウントデータの標本平均 |
| v1 <- sum(table(d)/s*(xp-m1)^2) | # カウント分布の分散 |
| v2 <- var(count) | # カウントデータの標本分散 |
| # | # |
| op <- par(mfrow = c(1, 2)) | # 横に2つのグラフを並べる |
| plot(x,y, col="red") | # 個体分布の表示 |
| abline(h=0, v=0) | # 外枠 |
| abline(h=1, v=1) | # 外枠 |
| for(i in 1:m) abline(h=i/m, v=i/m, lty=2) | # メッシュ区分線 |
| plot(xp, table(d)/s, type="h") | # 区分された分布のグラフ |
| lam <- n/(m*m) | # 平均 |
| yp <- dpois(xp, lam) | # ポアソン分布確率密度 |
| points(xp, yp, type="b", col="red") | # ポアソン分布グラフ表示 |
| par(op) | # グラフ表示もとに戻す |
| title(main="区画内個体数へのポアソン分布のあてはめ(平均:2)") | # タイトル |
| m1 | # カウント分布平均 |
| v1 | # カウント分布分散 |
| (4. 5) |
| 虫歯の数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| 児童の数 | 4 | 9 | 16 | 13 | 9 | 7 | 5 | 4 | 3 |
虫歯数データが負の二項分布に従っていると仮定する.虫歯データの平均は3.3286,分散は4.3063,
であった.負の二項分布は2つのパラメータ n,p を持つのでそれをデータから推定する必要がある.
分布パラメータの推定法は後に詳しく議論するが,ここでは直感的に理解しやすいモーメント法を説明
する.これは,分布の平均や分散などのモーメントがデータの平均や分散と等しい,とおくことでパラメータ
の推定を行う方法である.
課題:負の二項分布の確率密度は dnbinom(x, n, p) で与えられる.モーメント法を用いてパラメータ n,p の値を推定し,この推定値を用いて,児童の虫歯データに負の二項分布をあてはめたグラフ (下図のようなもの)を描け.
モーメント法による推定値を用いて,虫歯数データに負の二項分布をあてはめた.データは分布にまあまあ 適合しているようにみえる.
| x <- 0:10 | #グラフのx軸の範囲 |
| y <- c(4,9,16,13,9,7,5,4,3,0,0) | #虫歯数 |
| s <- sum(y) | #虫歯数の総和 |
| m <- sum(x*y/s) | #平均 |
| v <- sum((x-m)^2*y/s) | #分散 |
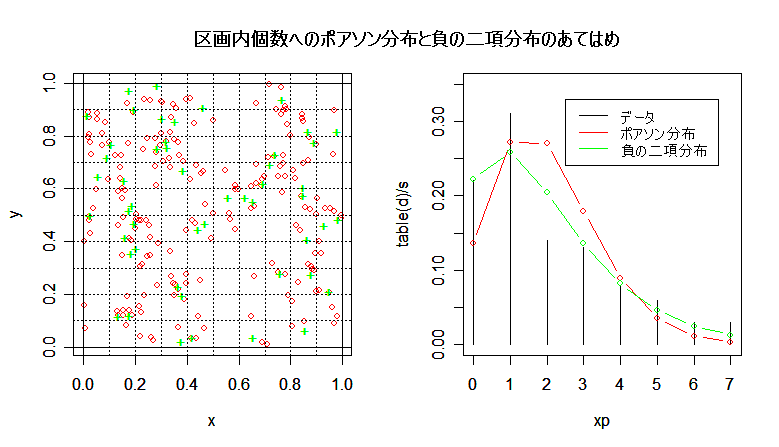
| n <- 200 | # 個体数(予定) |
| m <- 10 | # メッシュ(m2 個) |
| p <- 4 | # 平均子ども数 |
| sig <- 0.05 | # 正規分布標準偏差 |
| xx <- NULL | # xx(子ども座標)の定義 |
| xx0 <- NULL | # xx0(親座標)の定義 |
| np <- round(n/p) | # 親の数(round() は 5 捨 6 入) |
| for(i in 1:np){ | # np 回の繰り返し |
| x0 <- runif(2) | # 親個体の座標を一様乱数で生成 |
| n0 <- rpois(1, p) | # 子どもの数を平均 p のポアソン乱数で生成 |
| for(j in 1:n0){ | # n0 回の繰り返し |
| xd <- rnorm(2, m=x0, sd=sig) | # 子どもの座標を,正規乱数 N(x0, sig2)で生成 |
| if(xd[1] > 1) xd[1] <- xd[1] - 1 | # x 座標が 1 を超えたとき区画の左端に |
| if(xd[1] < 0) xd[1] <- xd[1] + 1 | # x 座標が 0 未満のとき区画の右端に |
| if(xd[2] > 1) xd[2] <- xd[2] - 1 | # y 座標が 1 を超えたとき区画の下辺に |
| if(xd[2] < 0) xd[2] <- xd[2] + 1 | # y 座標が 0 未満のとき区画の上辺に |
| xx <- rbind(xx, xd) | # 個体座標行列の行の追加 |
| xx0 <- rbind(xx0, x0) | # 個体座標行列の行の追加 |
| } | # |
| } | # |
| # 区画内個体数 | # |
| x <- xx[,1]; y <- xx[,2] | # x 座標ベクトル,y 座標ベクトル |
| count <- NULL | # count の定義 |
| for(i in 1:m){ | # m 回の繰り返し |
| n1 <- (1:n)[x < (i-1)/m] | # (i-1)/m 以下の乱数である番号 |
| n2 <- (1:n)[x < i/m] | # i/m 以下の乱数である番号 |
| nin <- n2[!n2 %in% n1] | # (i-1)/m から i/m の番号 |
| yy <- y[nin] | # 上記 x 座標に対する y 座標 |
| a <- hist(yy, breaks=0:m/m) | # yy を 0 から 1 まで 1/m きざみで区切る |
| count <- c(count, a$counts) | # 区切った領域に入った個体の個数のベクトル |
| } | # |
| mc <- max(count) | # メッシュ内の個数の最大値 |
| xp <- 0:mc | # 個数の定義域 |
| d <- factor(count, levels=xp) | # 個数が 0 の階級も含める |
| table(d) | # メッシュ内個数の階級区分 |
| s <- sum(table(d)) | # 総個体数 |
| m1 <- sum(xp*table(d)/s) | # カウント分布の平均 |
| v1 <- sum(table(d)/s*(xp-m1)^2) | # カウント分布の分散 |
| # | # |
| op <- par(mfrow = c(1, 2)) | # 横に2つのグラフを並べる |
| plot(x,y, col="red") | # 個体分布の表示 |
| points(xx0, pch="+", col="green") | # 個体分布の表示 |
| abline(h=0, v=0) | # 外枠 |
| abline(h=1, v=1) | # 外枠 |
| for(i in 1:m) abline(h=i/m, v=i/m, lty=3) | # メッシュ区分線 |
| plot(xp, table(d)/s, type="h", ylim=c(0,0.35)) | # 区分された分布のグラフ |
| yp <- dpois(xp, m1) | # ポアソン分布確率 |
| points(xp, yp, type="b", col="red") | # ポアソン分布表示 |
| nbp <- m1/v1 | # |
| nbn <- m1*nbp/(1-nbp) | # |
| ynb <- dnbinom(xp, nbn, nbp) | # 負の二項分布確率 |
| points(xp, ynb, type="b", col="green") | # 負の二項分布表示 |
| legend(2.5, 0.33, c("データ", "ポアソン分布", "負の二項分布"), lty=1, col=c("black","red","green")) | |
| par(op) | # 個体数 |
| title(main="区画内個数へのポアソン分布と負の二項分布のあてはめ") | |
| m1 | # 平均 |
| v1 | # 分散 |
課題:平均子ども数である p の値を増やすとどうなるか.
| データ | 適応する分布 | 平均 | 分散 |
|---|---|---|---|
| 平均>分散 | 二項分布 | np | np(1 - p) |
| 平均≒分散 | ポアソン分布 | λ | λ |
| 平均<分散 | 負の二項分布 | n(1 - p)/p | n(1 - p)/p2 |
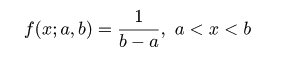
| (4. 6) |
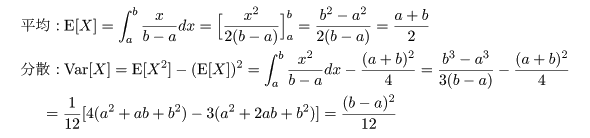
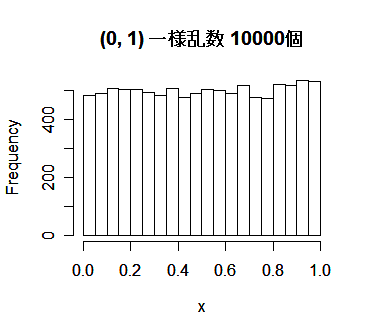
| x <- runif(10000) | #(0,1)一様乱数1000個列 |
| hist(x, main="(0, 1) 一様乱数 10000個") | #ヒストグラム表示 |
| n <- 10000 | #一様乱数の個数 |
| x <- runif(n, -1, 1) | #(-1, 1) の範囲の一様乱数 n 個生成 |
| y <- runif(n, -1, 1) | # |
| r <- x^2 + y^2 | #原点からの距離の2乗 |
| plot(x,y, type="n", xlim=c(-1,1), ylim=c(-1,1)) | #グラフの表示範囲の指定 |
| abline(h=0) | # x 軸の表示 |
| abline(v=0) | # y 軸の表示 |
| segments(-1, 1, 1, 1) | #(-1, 1)から(1, 1)までの直線 |
| segments(1, 1, 1, -1) | # |
| segments(-1, -1, 1, -1) | # |
| segments(-1, -1, -1, 1) | # |
| pin <- (1:n)[r<1] | #乱数のうち単位円内に入る乱数の番号 |
| points(x[-pin], y[-pin], pch=".", col="green") | #単位円の外の乱数を緑点で表示 |
| points(x[pin], y[pin], pch=".", col="red") | #単位円内の乱数を赤い点で表示 |
| s <- 0:360 | # 0 度から 360 度 |
| theta <- s*pi/180 | #度をラジアンに変換 |
| xp = sin(theta) | #単位円の x 座標 |
| yp = cos(theta) | #単位円の y 座標 |
| points(xp,yp, type="l") | #単位円を表示 |
| title(main="(-1,1)一様乱数による点列と単位円") | |
| length(pin) | #単位円内に入った乱数の個数 |
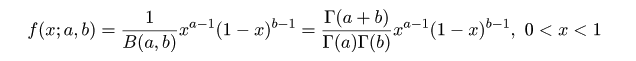
| (4. 7) |
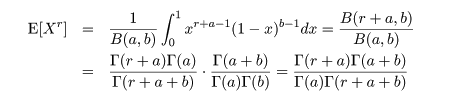
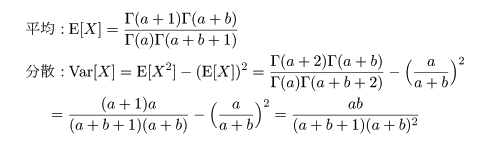
|
|
|
| x <- seq(0,1, by=0.01) | # x の定義 0 から 1 まで 0.01 きざみ |
| y <- dbeta(x, 0.5, 0.5) | # a, b = 0.5, 0.5 のβ分布 |
| plot(x, y, type="l", ylim=c(0,3), col="red") | # y を 0 から 3 に指定(赤) |
| abline(v=0, h=0) | # y 軸と x 軸の表示 |
| curve(dbeta(x, 1, 1), 0, 1, add=T) | # a, b = 1, 1 のβ分布 |
| curve(dbeta(x, 2, 2), 0, 1, add=T, col="blue") | # a, b = 2, 2 のβ分布(青) |
| curve(dbeta(x, 1, 3), 0, 1, add=T, col="green") | # a, b = 1, 3 のβ分布(緑) |
| curve(dbeta(x, 2, 4), 0, 1, add=T, col="purple") | # a, b = 2, 4 のβ分布(紫) |
| title(main="β分布") | # |
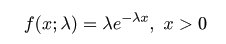
| (4. 8) |
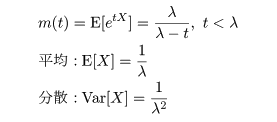
| curve(dexp(x, 1), 0, 10) | #指数分布の密度関数 |
| abline(v=0, h=0) | # y 軸,x 軸表示 |
| title(main="指数分布") | # |
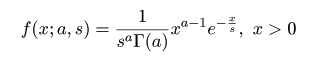
| (4. 9) |
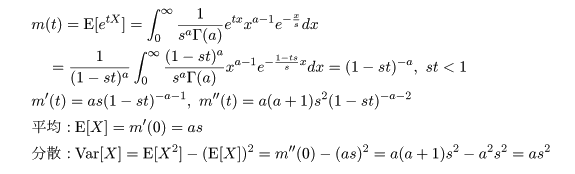
|
|
|
課題: Γ 分布の確率密度は dgamma(x, a, 1/s),もしくは,dgamma(x, shape=a, scale=s) で 与えられる.Γ 分布のパラメータを変えて,上の図のようなグラフを描け.
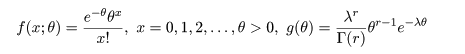
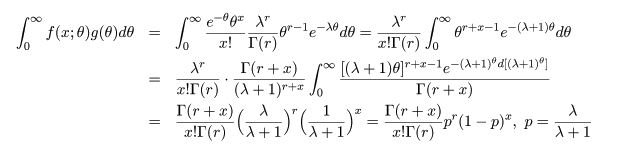
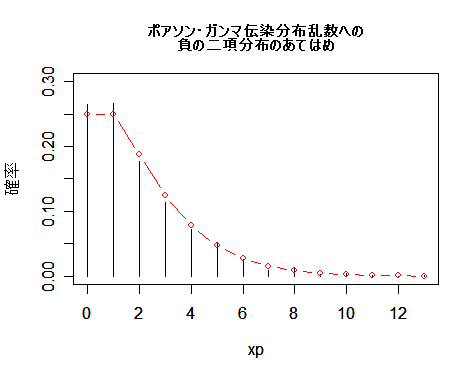
| n <- 1000 | # 伝染分布乱数の個数 |
| count <- NULL | # count の定義 |
| for(i in 1:n){ | # n 回の繰り返し |
| r <- 2 | # ガンマ分布のシェープパラメータ |
| lam <- 1 | # ガンマ分布のレイトパラメータ |
| theta <- rgamma(1, r, lam) | # ガンマ分布乱数1つ生成 |
| count <- c(count, rpois(1, theta)) | # 生成乱数をパラメータにするポアソン乱数列 |
| } | # |
| mc <- max(count) | # ポアソン・ガンマ乱数列の最大値 |
| xp <- 0:mc | # 個数の定義域 |
| d <- factor(count, levels=xp) | # 個数が 0 の階級も含める |
| table(d) | # メッシュ内個数の階級区分 |
| s <- sum(table(d)) | # 総個体数 |
| m1 <- sum(xp*table(d)/s) | # カウント分布の平均 |
| v1 <- sum(table(d)/s*(xp-m1)^2) | # カウント分布の分散 |
| plot(xp, table(d)/s, type="h", ylim=c(0,0.3), ylab="確率") | # ポアソン・ガンマ乱数のグラフ |
| p <- lam/(lam+1) | # 負の二項分布確率パラメータ |
| ynb <- dnbinom(xp, r, p) | # 負の二項分布確率密度 |
| points(xp, ynb, type="b", col="red") | # 負の二項分布のグラフ |
| title(main="ポアソン・ガンマ伝染分布乱数への\n負の二項分布のあてはめ", cex.main=0.8) | |
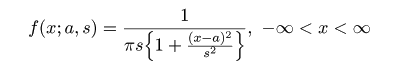
| (4.10) |
| curve(dcauchy(x), -5, 5) | #コーシー分布の密度関数 |
| abline(v=0, h=0) | # y 軸,x 軸表示 |
| title(main="コーシー分布") | # |
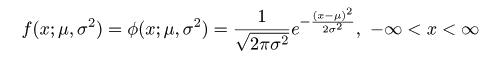
| (4.11) |
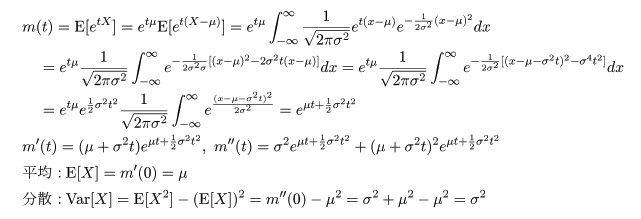
 |
 |
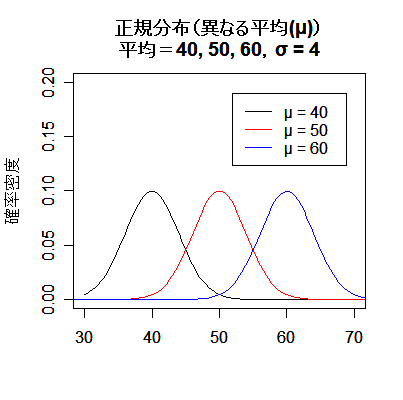
| # 平均の異なる正規分布 | |
| curve(dnorm(x, 40, 4), 30, 70, ylim=c(0,0.2), xlab="",ylab="確率密度") | # 平均:40,標準偏差:4 |
| curve(dnorm(x, 50, 4), add=TRUE, col="red") | # 平均:50,標準偏差:4 |
| curve(dnorm(x, 60, 4), add=TRUE, col="blue") | # 平均:60,標準偏差:4 |
| title(main="正規分布(異なる平均(μ))\n平均=40, 50, 60,σ = 4") | # タイトル |
| legend(52,0.19,c("μ = 40","μ = 50","μ = 60"), lty=1, col=c("black","red","blue")) | # 凡例 |
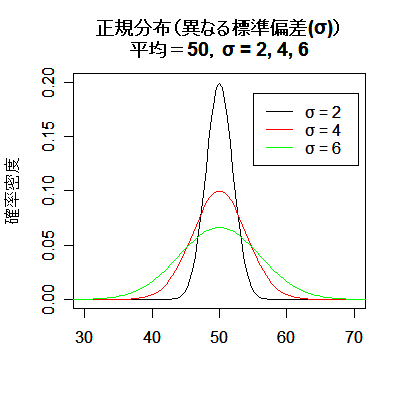
| # 標準偏差(分散)の異なる正規分布 | |
| curve(dnorm(x, 50, sd=2), 30, 70, ylim=c(0,0.2), xlab="",ylab="確率密度") | # 平均:50,標準偏差:2 |
| curve(dnorm(x, mean=50, sd=4), add=TRUE, col="red") | # 平均:50,標準偏差:4 |
| curve(dnorm(x, mean=50, sd=6), add=TRUE, col="green") | # 平均:50,標準偏差:6 |
| title(main="正規分布(異なる標準偏差(σ))\n平均=50,σ = 2, 4, 6") | # タイトル |
| legend(55,0.19,c("σ = 2","σ = 4","σ = 6"), lty=1, col=c("black","red","green")) | # 凡例 |
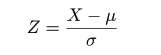
| (4.12) |
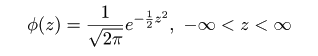
| (4.13) |
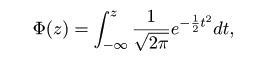
| (4.14) |
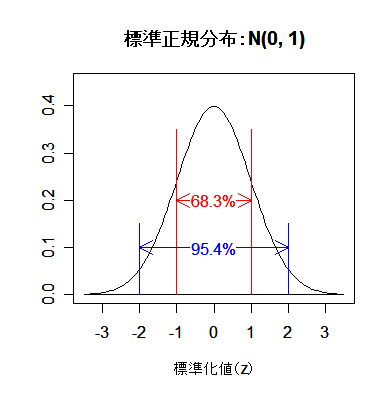 |
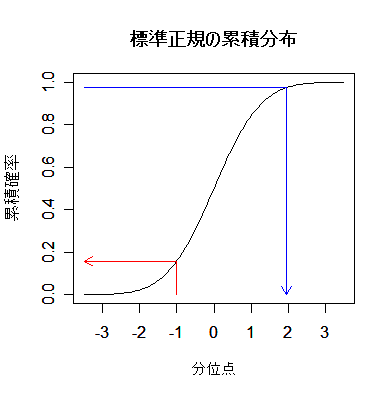 |
| pnorm(-1) | # = 0.16(赤矢印) |
| pnorm(1) - pnorm(-1) | # = 0.683 |
| pnorm(2) - pnorm(-2) | # = 0.954 |
| qnorm(0.975) | # = 1.96(青矢印),両側 5 %点 |
| 身長 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 |
|---|---|---|---|---|---|---|---|---|---|---|
| 人数 | 2 | 4 | 14 | 41 | 83 | 169 | 394 | 669 | 990 | 1223 |
| 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 |
| 1329 | 1230 | 1063 | 646 | 392 | 202 | 79 | 32 | 16 | 5 | 2 |
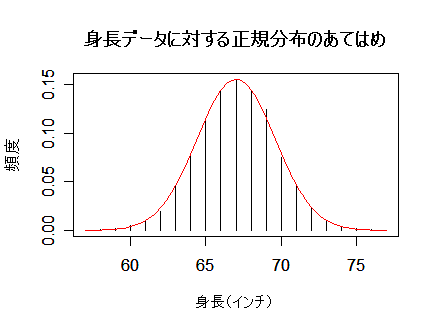
| x <- 57:77 | # 身長(x)の範囲 |
| y <- c(2, 4, 14, 41, 83, 169, 394, 669, 990, 1223, 1329, | # 身長ごとのデータ |
| 1230, 1063, 646, 392, 202, 79, 32, 16, 5, 2) | # |
| s <- sum(y) | # データ総数 |
| m <- sum(x*y/s); m | # データの平均 |
| v <- sum(y/s*(x-m)^2); v | # データの分散 |
| plot(x, y/s, type="h", xlab="身長(インチ)", ylab="頻度") | # データの棒グラフ表示 |
| curve(dnorm(x, m, sqrt(v)), 57, 77, add=T, col="red") | # 正規密度のグラフ表示 |
| title(main="身長データに対する正規分布のあてはめ") | # タイトル |
| m <- 67.02; s <- 2.556 | # 平均と標準偏差の指定 |
| 1 - pnorm(70, mean=m, sd=s) | # 1. 70 までの累積確率を 1 から引く |
| qnorm(0.9, mean=m, sd=s) | # 2. 累積確率が 0.9 となる身長 |
| pnorm(70, mean=m, sd=s) - pnorm(65, mean=m, sd=s) | # 3. (70 までの累積確率) − (60 までの累積確率) |
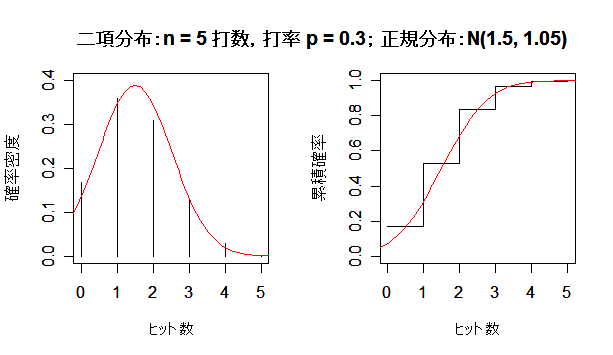
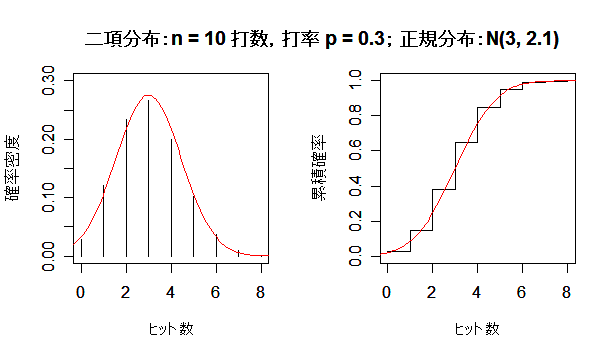
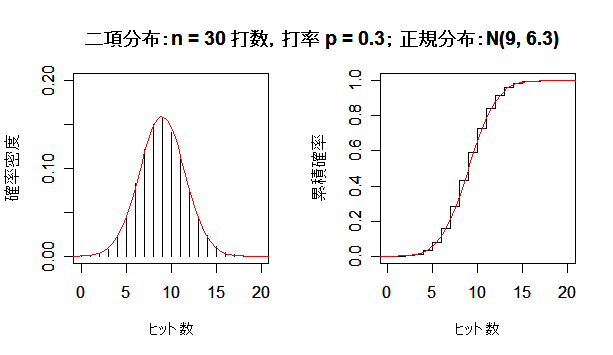
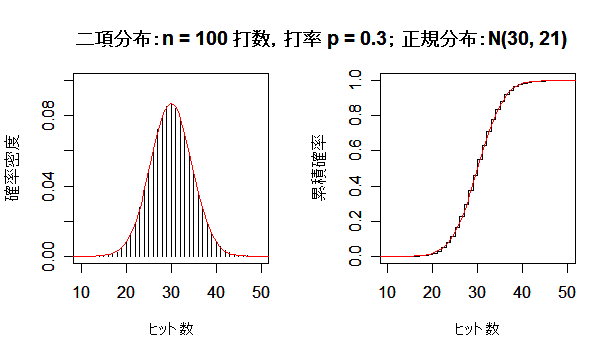
| n <- 5 | # 打数 |
| x <- 0:n | # xの範囲 |
| p <- 0.3 | # 打率 |
| hit <- dbinom(x, size=n, prob=0.3) | # 二項確率 |
| y <- pbinom(x, size=n, prob=0.3) | # 二項累積確率 |
| m <- n*p | # 平均 |
| sd <- sqrt(n*p*(1-p)) | # 標準偏差 |
| op <- par(mfrow = c(1, 2)) | # |
| plot(x, hit, type="h", ylim=c(0,0.4), xlim=c(0,7), xlab="ヒット数", ylab="確率密度") | |
| curve(dnorm(x, mean=m, sd=sd), add=TRUE, col="red") | # 確率密度 |
| plot(x, y, type="s", ylim=c(0,1), xlim=c(0,7), xlab="ヒット数", ylab="累積確率") | |
| curve(pnorm(x, mean=m, sd=sd), add=TRUE, col="red") | # 累積確率 |
| par(op) | # |
| title(main ="二項分布:n = 5 打数,打率 p = 0.3; 正規分布:N(1.5, 1.05) ") | |
課題:打数 n を大きくして,二項分布が正規分布に近づく様子を確かめよ.
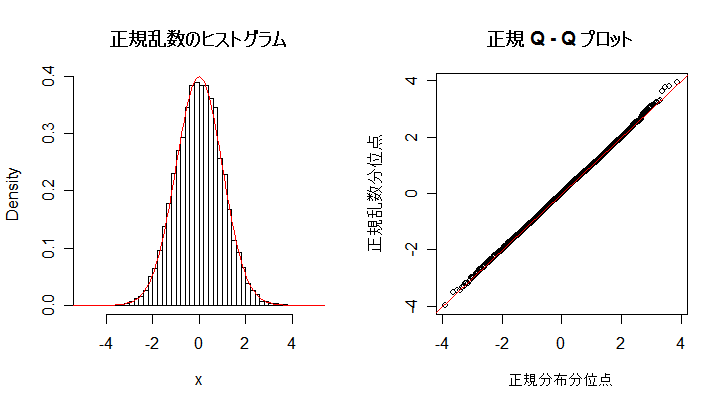
| n <- 10000 | # 乱数列の長さ |
| x <- rnorm(n) | # 標準正規乱数 |
| op <- par(mfrow = c(1, 2)) | # |
| hist(x, breaks=seq(-10,10, by=0.2), xlim=c(-5,5),freq=F, main="") | # 乱数のヒストグラム |
| curve(dnorm(x), add=T, col=2) | # 標準正規分布の重ね合わせ |
| title(main="正規乱数のヒストグラム") | # タイトル |
| qqnorm(x, xlab="正規分布分位点", ylab="正規乱数分位点", main="") | # 正規 Q - Q プロット |
| qqline(x, col=2) | # 正規分布の四分位範囲直線表示 |
| title(main="正規 Q - Q プロット") | # タイトル |
| par(op) | # |
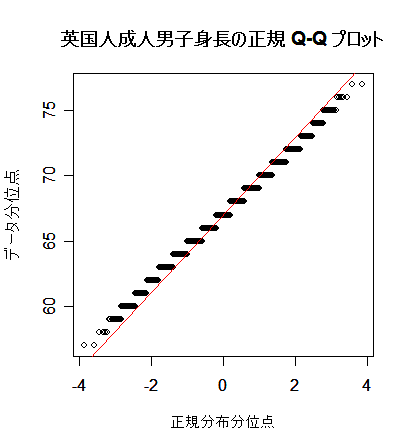
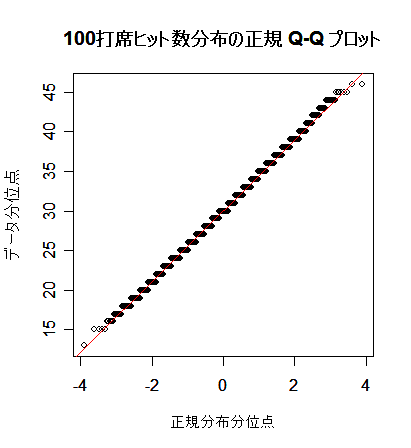
次に, 英国人成人身長データと二項分布を正規分布にあてはめた場合について,正規分布との適合性 を正規 Q - Q プロットでみてみよう.左下図は,身長データの正規 Q - Q プロットで,正規分布から 少しずれている様子がわかる.右下図は,打率 p = 0.3 の選手の n = 100 打席でのヒット数の分布 で,正規分布によくフィットしているのがよくわかる.
 |
 |
 |
 |
 |
| N <- 10000 | # 乱数列の長さ |
| n <- 2 | # 標本平均のサイズ |
| u <- matrix(data=runif(n*N), ncol=n) | # N×n の一様乱数行列 |
| um <- apply(u, 1, mean) | # 行ごとの平均 |
| op <- par(mfrow = c(1, 2)) | # 標本平均のヒストグラム |
| hist(um, breaks=seq(0,1,by=0.02), freq=FALSE, ylim=c(0, 2.5), xlab="", ylab="頻度", main="") | |
| m <- mean(um) | # 標本平均列の平均 |
| s <- sd(um) | # 標本平均列の標準偏差 |
| curve(dnorm(x, m, s), 0, 1, add=TRUE, col="red") | # 正規分布の重ねがき |
| qqnorm(um, xlab="正規分布分位点", ylab="データ分位点", main="") | # 正規 Q - Q プロット |
| qqline(um, col="red") | # 正規分布の四分位範囲直線表示 |
| par(op) | # |
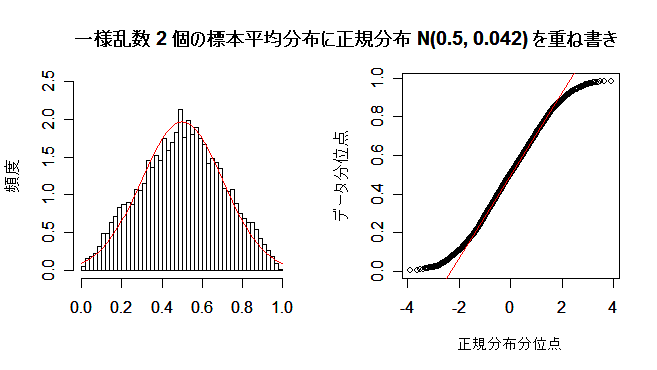
| title(main="一様乱数 2 個の標本平均分布に正規分布 N(0.5, 0.042) を重ね書き") | |
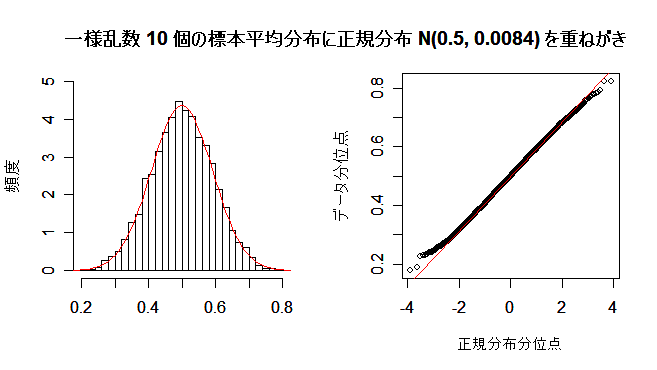
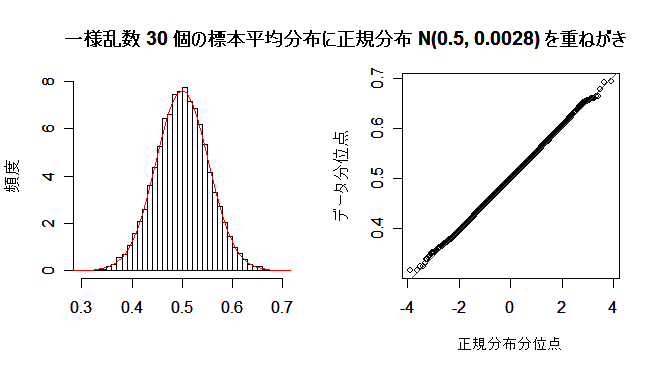
課題:サンプルサイズ n を大きくして,標本平均の分布が正規分布に近づく様子を確かめよ.
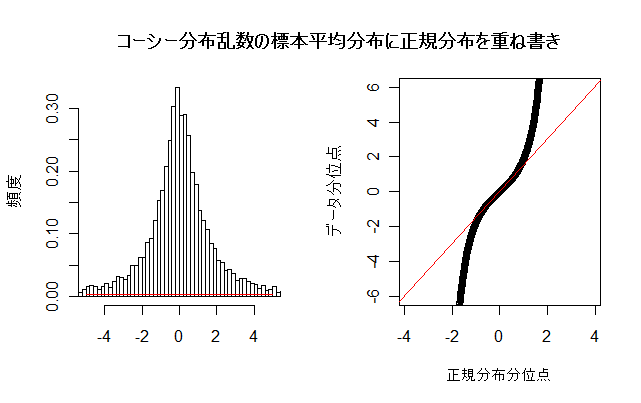
N <- 10000 # 乱数列の長さ n <- 100 # 標本平均のサイズ u <- matrix(data=rcauchy(n*N), ncol=n) # N×n のコーシー分布乱数行列 um <- apply(u, 1, mean) # 行ごとの平均 min(um) # 平均値の最小値 max(um) # 平均値の最大値 uma <- floor(min(um)) umb <- ceiling(max(um)) op <- par(mfrow = c(1, 2)) # 標本平均のヒストグラム hist(um, breaks=seq(uma,umb,by=0.2), xlim=c(-5,5), freq=FALSE, xlab="", ylab="頻度", main="") m <- mean(um); m # 標本平均列の平均 s <- sd(um); s # 標本平均列の標準偏差 curve(dnorm(x, m, s), -5, 5, add=TRUE, col="red") # 正規分布の重ねがき qqnorm(um, xlab="正規分布分位点", ylim=c(-6,6), ylab="データ分位点", main="") # 正規 Q - Q プロット qqline(um, col="red") # 正規分布の四分位範囲直線表示 par(op) title(main="コーシー分布乱数の標本平均分布に正規分布を重ね書き") |
課題:コーシー分布乱数のメデイアンの分布を正規分布にあてはめたときはどうなるか.
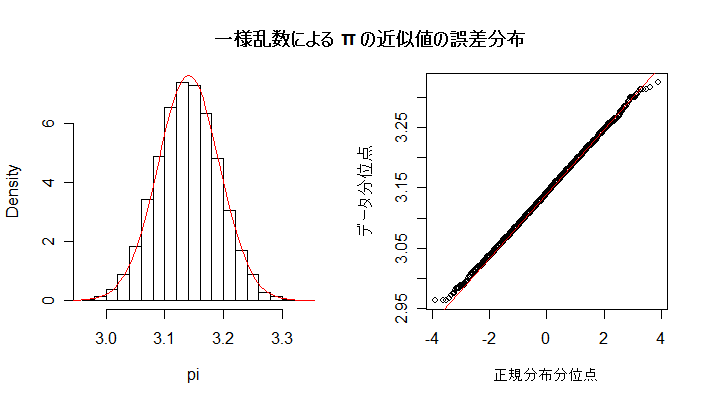
| N <- 10000 | # 点セット列の長さ |
| n <- 1000 | # 乱数点の個数 |
| pi <- NULL | # pi の定義 |
| for(i in 1:N){ | # N 回の繰り返し |
| x <- runif(n, -1, 1) | # (-1, 1) の範囲の一様乱数 n 個生成 |
| y <- runif(n, -1, 1) | # |
| r <- x^2 + y^2 | # 原点からの距離の2乗 |
| pi <- c(pi, 4*length(r[r<1])/n) | # πの近似値ベクトル |
| } | # |
| m = mean(pi) | # 近似値の平均 |
| s = sd(pi) | # 近似値の標準偏差 |
| m | # 平均の表示 |
| s | # 標準偏差の表示 |
| op <- par(mfrow = c(1, 2)) | # |
| hist(pi, freq=F, main="") | # 近似値のヒストグラム |
| curve(dnorm(x, m, s), 2.9, 3.4, add=T, col=2) | # 正規分布の重ね合わせ |
| qqnorm(pi, xlab="正規分布分位点", ylab="データ分位点", main="") | # 正規 Q - Q プロット |
| qqline(pi, col="red") | # 正規分布の直線表示 |
| par(op) | # |
| title(main="一様乱数による π の近似値の誤差分布") | # タイトル |
レポート1:乱数点の個数 n を大きくしたとき,誤差の大きさの減少の程度を n のオーダー で表せ.
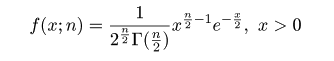
| (4.15) |
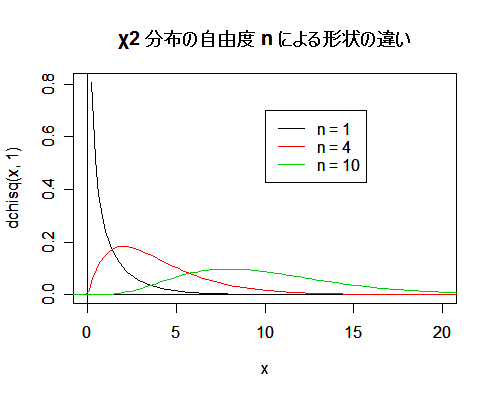
| curve(dchisq(x, 1), 0, 20) | # 自由度 1 の χ2 分布のグラフの表示 |
| abline(v=0, h=0) | # x 軸と y 軸の表示 |
| curve(dchisq(x, 4), add=T, col=2) | # 自由度 4 の χ2 分布のグラフを色 2(赤)で追加 |
| curve(dchisq(x, 10), add=T, col=3) | # 自由度 10 の χ2 分布のグラフを色 3(緑)で追加 |
| legend(10, 0.7, c("n = 1", "n = 4", "n = 10"), lty=1, col=c(1, 2, 3)) | |
| title(main="χ2 分布の自由度 n による形状の違い") | # タイトル |
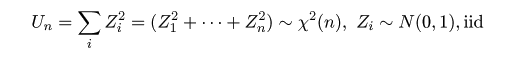
| (4.16) |
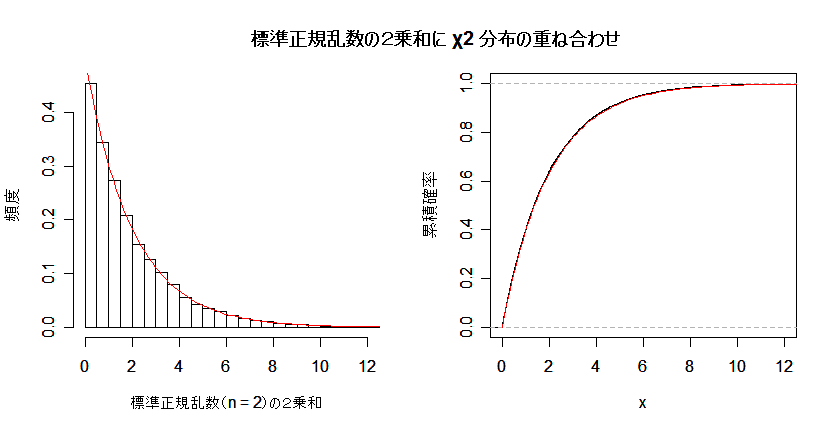
| N <- 10000 | # 乱数列の長さ |
| n <- 2 | # 自由度 |
| u <- matrix(rnorm(n*N), ncol=n) | # N×n の標準正規乱数乱数行列 |
| u2 <- u^2 | # 行列の要素の2乗 |
| un <- apply(u2, 1, sum) | # 行ごとの和 |
| umx <- ceiling(max(un)) | # 最大値を超える整数 |
| op <- par(mfrow = c(1, 2)) | # |
| hist(un, breaks=seq(0,umx,by=0.5), freq=FALSE, xlim=c(0,15), xlab="標準正規乱数(n = 2)の2乗和", ylab="頻度", main="") | |
| curve(dchisq(x, n), 0, 15, add=T, col=2) | # 自由度 2 の χ2 分布の重ね合わせ |
| plot(ecdf(un), do.points=F, verticals=T, xlim=c(0,12), ylab="累積確率", main="") | |
| curve(pchisq(x,2), 0, 15, add=T, col=2) | # 自由度 2 の χ2 累積分布関数の重ね合わせ |
| par(op) | # |
| title(main="標準正規乱数の2乗和に χ2 分布の重ね合わせ") | # タイトル |
課題:2乗和する数 n を大きくした場合も,標準正規乱数の2乗和の分布が 自由度 n の χ2 分布に従うことを確かめよ.
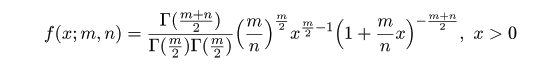
| (4.17) |
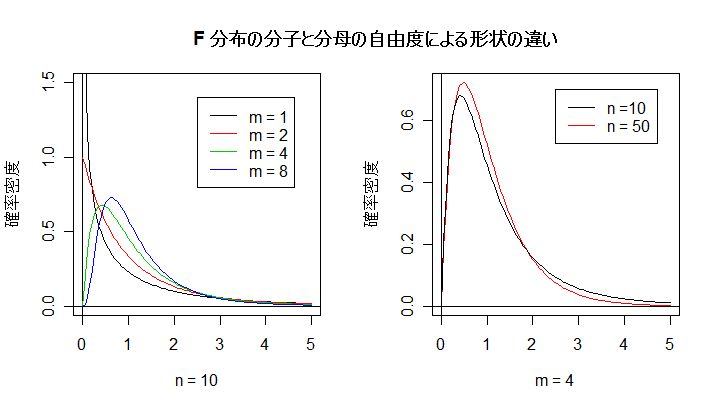
| op <- par(mfrow = c(1, 2)) | # |
| curve(df(x, 1, 10), 0, 5, ylim=c(0,1.5), ylab="確率密度", xlab="n = 10") | # m = 1,n = 10 の F 分布 |
| abline(v=0, h=0) | # x 軸,y 軸 |
| curve(df(x, 2, 10), 0, 5, add=T, col=2) | # m = 2,n = 10 の F 分布 |
| curve(df(x, 4, 10), 0, 5, add=T, col=3) | # m = 4,n = 10 の F 分布 |
| curve(df(x, 8, 10), 0, 5, add=T, col=4) | # m = 8,n = 10 の F 分布 |
| legend(2.5, 1.4, c("m = 1", "m = 2", "m = 4", "m = 8"), lty=1, col=1:4) | # 凡例 |
| curve(df(x, 4, 50), 0, 5, col=2, ylab="確率密度", xlab="m = 4") | # m = 4,n = 50 の F 分布 |
| abline(v=0, h=0) | # x 軸,y 軸 |
| curve(df(x, 4, 10), 0, 5, add=T) | # m = 4,n = 10 の F 分布 |
| legend(2.5, 0.7, c("n =10", "n = 50"), lty=1, col=c("black","red")) | # 凡例 |
| par(op) | # |
| title(main="F 分布の分子と分母の自由度の違いによる形状") | # タイトル |
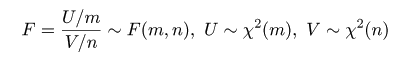
| (4.18) |
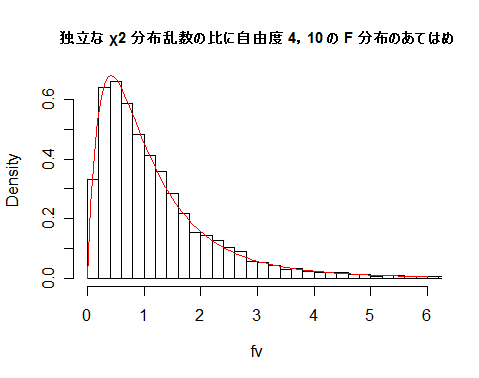
| N <- 10000 | # 乱数列の長さ |
| m <- 4 | # 分子自由度 |
| n <- 10 | # 分母自由度 |
| um0 <- matrix(rnorm(m*N), ncol=m) | # N×m の標準正規乱数乱数行列 |
| um2 <- um0^2 | # 行列の要素の2乗 |
| um <- apply(um2, 1, sum) | # 行ごとの和 |
| um <- um/m | # 自由度で割る |
| un0 <- matrix(rnorm(n*N), ncol=n) | # |
| un2 <- un0^2 | # |
| un <- apply(un2, 1, sum) | # |
| un <- un/n | # |
| fv <- um/un | # χ2 分布乱数の比 |
| fmx <- ceiling(max(fv)) | # fv の最大値を超える整数 |
| hist(fv, breaks=seq(0,fmx,by=0.2), freq=FALSE, xlim=c(0,6), main="") | |
| curve(df(x, m, n), 0, 6, add=T, col=2) | # 自由度 4,10 の F 分布の重ね合わせ |
| title(main="独立な χ2 分布乱数の比に自由度 4,10 の F 分布のあてはめ", cex.main=0.9) | |
課題:分子,分母の自由度を変えて,χ2 分布乱数の比が F 分布に従うことを確かめよ.
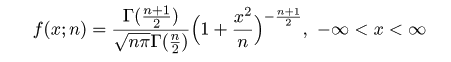
| (4.19) |
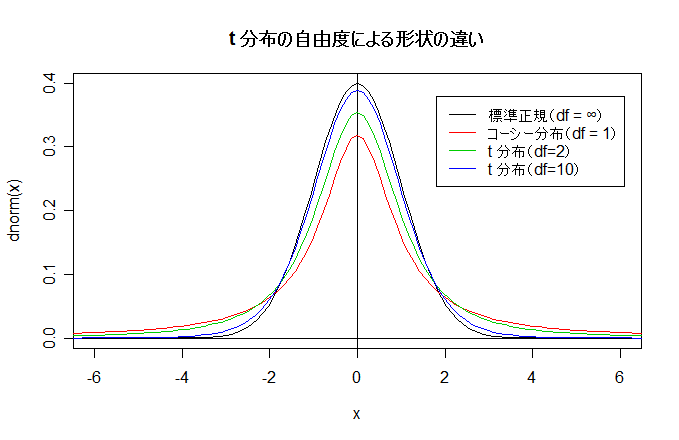
課題: t 分布の確率密度関数は,自由度を n として dt(x, n) で与えられる.n の値を変えることにより, 上の図のようなグラフを描け.
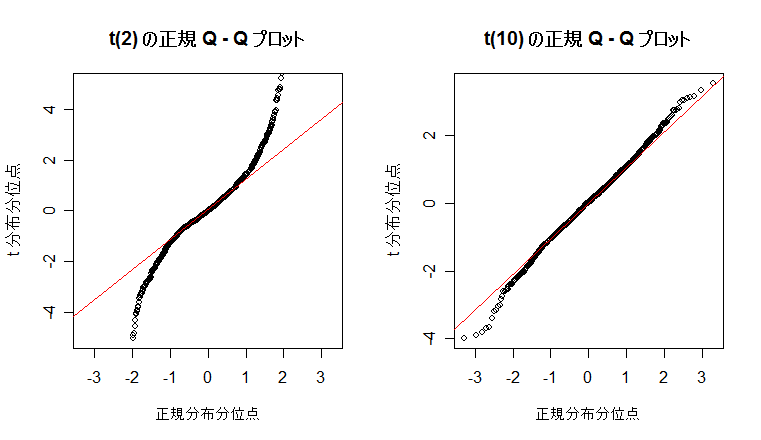
| N <- 10000; n <- 10 | # 乱数列の長さと自由度の設定 |
| y <- rt(N, df=n) | # 自由度 10 の t 分布乱数1000個生成 |
| qqnorm(y, xlab="正規分布分位点", ylab="t 分布分位点", main="") | # 正規 Q - Q プロット |
| qqline(y, col=2) | # 正規分布の四分位範囲直線表示 |
| title(main="t(10) の正規 Q - Q プロット") | # |
課題: 自由度を n の値を変えて,標準正規分布とのずれの様子を正規 Q - Q プロット で確かめよ.
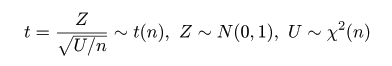
| (4.20) |
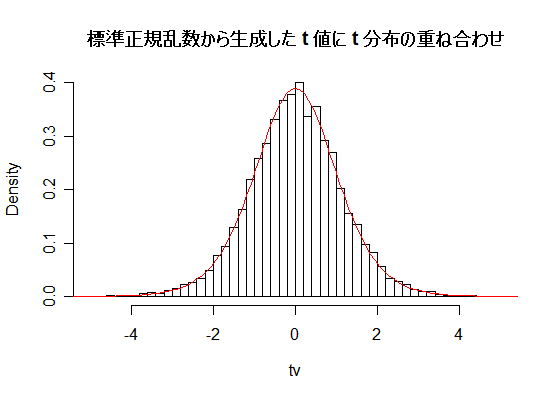
| N <- 10000 | # シミュレーション回数 |
| n <- 10 | # 1回のサンプルサイズ(自由度) |
| un0 <- matrix(rnorm(n*N), ncol=n) | # N×n の標準正規乱数行列 |
| un2 <- un0^2 | # 標準正規乱数行列の要素の2乗 |
| un <- apply(un2, 1, sum) | # 要素の2乗の各行の和(自由度 n の χ2 分布乱数 N 個) |
| unr <- sqrt(un/n) | # 自由度 n の χ2 分布乱数を n で割った平方根 |
| z <- rnorm(N) | # 標準正規乱数 N 個 |
| tv <- z/unr | # t 値 N 個 |
| tmx <- ceiling(max(abs(tv))) | # t 値 の絶対値の最大 |
| hist(tv, breaks=seq(-tmx,tmx,by=0.2), freq=FALSE, xlim=c(-5,5), main="") | |
| curve(dt(x, n), add=T, col=2) | # 自由度 10 の t 分布の重ねがき |
| title(main="標準正規乱数から生成した t 値に t 分布の重ね合わせ") | |