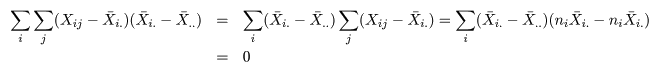
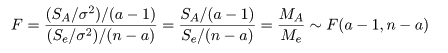
| 変動因 | 自由度(df) | 平方和(S.S.) | 平均平方(M.S.) | F 値 |
|---|---|---|---|---|
| 主効果 | a - 1 | SA | MA = SA/(a - 1) | MA/Me |
| 誤 差 | n - a | Se | Me = Se/(n - a) | |
| 全 体 | n - 1 | ST |
| yy <- read.csv("hinsyu.csv"); yy | # csv データ読み込み |
| n <- nrow(yy) | # 繰り返し数 |
| a <- ncol(yy) | # 処理数 |
| y <- NULL; x <- NULL | # |
| for(i in 1:a){ | # |
| x <- c(x, rep(i, n)) | # 品種番号ベクトル |
| y <- c(y, yy[,i]) | # 収量データベクトル |
| } | # |
| x <- factor(x) | # ラベル化 |
| cbind(y,x) | # ベクトルデータ表示 |
| summary(aov(y ~ x)) | # 一元配置分散分析 |
| anova(lm(y ~ x)) | # 一元配置分散分析(これでもよい) |
| # 分散分析の計算を以下で詳しくみる | |
| nn <- length(y) | # 総データ数 |
| s <- diag(var(yy)*(n-1)) | # 各品種内誤差 |
| se <- sum(s); se | # 誤差平方和 |
| st <- var(y)*(nn-1) | # 総平方和 |
| sa <- st - se; sa | # 処理平方和 |
| va <- sa/(a - 1); va | # 処理平均平方 |
| ve <- se/(nn - a); ve | # 誤差平均平方 |
| fv <- va/ve; fv | # F 値 |
| pv <- 1 - pf(fv, df1=(a-1), df2=(nn-a)); pv | # p 値 |
| # データの品種ごとのちらばりと,品種平均と標準誤差を視覚化する | |
| xm <- 1:9 | # |
| ym <- mean(yy) | # 品種ごとの平均 |
| vm <- ve/n | # 品種平均の分散 |
| svm <- sqrt(vm) | # 品種平均の標準誤差 |
| stripchart(yy, xlab="玄米重(kg/a)") | # 品種ごとの個体分布表示 |
| text(ym, xm,"|", col="red") | # 品種平均 |
| text(ym+svm, xm,"|", col="red") | # 品種平均 + 標準誤差 |
| text(ym-svm, xm,"|", col="red") | # 品種平均 − 標準誤差 |
| segments(ym-svm, xm, ym+svm, xm, col="red") | # 横線 |
| title(main="水稲品種収量個体分布") | # |
| 変動因 | 自由度(df) | 平方和(SS) | 平均平方(MS) | F 値 |
|---|---|---|---|---|
| 主効果 | 8 | 66.17 | 8.27 | 5.99 *** |
| 誤 差 | 45 | 62.09 | 1.38 | |
| 全 体 | 53 | 128.26 |
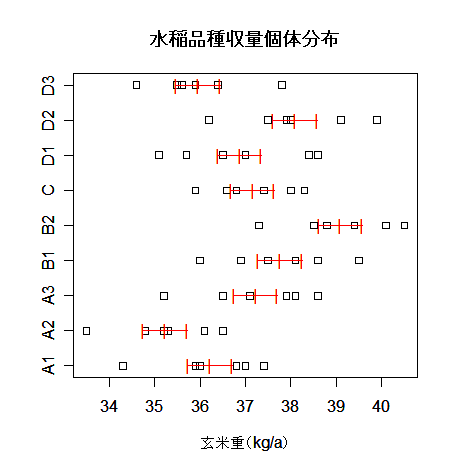
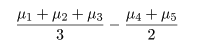
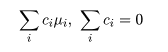
対比 C = Σiciμi は C^ = ΣiciX-i. で推定されるが, 帰無仮説(αi = 0)のもとでは, 対比推定量の平均と分散は,
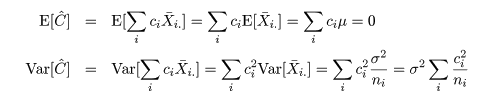
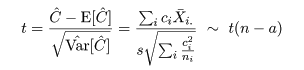
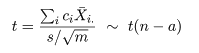
ところで,別の対比 Σidiμi があったときに, Σici di = 0,となるものを直交対比という. 直交対比の組は同時に検定ができる. 事前に比較が決められるときは,後述する多重比較による有意確率の補正を行わないことが多いと思われる.
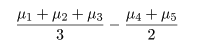
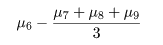
対比の検定の結果,母本 A と B の差は強度に有意(0.1%以下)であり,母本 A からの系統 の方が収量が高いと言える.また,標準品種 C と母本 D の系統では,有意な差が認められなかった.
| c1 <- c(1/3,1/3,1/3,-1/2,-1/2, 0, 0, 0, 0) | # 母本 A と B の平均の差の対比係数ベクトル |
| c2 <- c(0, 0, 0, 0, 0, 1,-1/3,-1/3,-1/3) | # 標準品種 C と母本 D の平均の差の対比係数ベクトル |
| contrasts(x) <- cbind(c1, c2) | # 品種ラベルに対比を定義する. |
| contrasts(x) | # 定義した残りの直交対比は R が勝手につくる |
| fc <- lm(y ~ x) | # 対比つき線形モデル |
| summary(fc) | # 結果表示(最初の2つの対比のみに着目) |
| # 対比の計算を詳しくみる | |
| gm <- tapply(y, x, mean); gm | # 品種平均 |
| cmat <- contrasts(x)[,1:2] | # 対比係数ベクトルの必要部分 |
| mc <- diag(t(cmat) %*% cmat) | # 対比係数ベクトルの長さの2乗 |
| esd <- summary(fc)$sigma | # 誤差標準偏差の推定値 |
| csd <- sqrt(mc)*esd/sqrt(n) | # 対比の標準誤差 |
| ce <- t(cmat) %*% gm | # 対比推定値(母本平均の差) |
| tv <- ce/csd; tv | # 対比 t 値 |
| 2*(1 - pt(abs(tv), df=(nn-a))) | # 対比 p 値 |
| ce <- ce/mc; ce | # 対比係数ベクトルの長さで補正した対比推定値 |
| csd <- csd/mc; csd | # 対比係数ベクトルの長さで補正した対比標準誤差 |
前節の対比でも,考えられる対比を無原則に行うときは多重比較の問題を考慮しなければならないが,この節
では対比の中でも最も単純な対比較(pairwise comparison),すなわち,
個々の処理水準間の比較のみを取り上げる.
いま,処理平均 μi と μj の比較を行う場合を考える.
2 つの処理平均の差 μi - μj は,
dij = X-i. - X-j. で推定される.
帰無仮説(αi = αj = 0)のもとで,dij の平均と分散は,
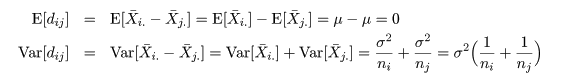
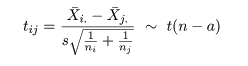
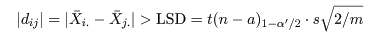
| pth <- pairwise.t.test(y, x); pth | # 対比較ホルム補正 |
| ptb <- pairwise.t.test(y, x, p.adj = "bonf"); ptb | # 対比較ボンフェローニ補正 |
| ptn <- pairwise.t.test(y, x, p.adj = "none"); ptn | # 対比較補正なし |
| showpt.f <- function(x, p){ | # p 値が p 以下の比較を表示する関数 |
| pl <- which(x < p, arr.ind=TRUE) | # 行列 x の要素が p 以下の場所 |
| cbind(pl[,2], x[pl]) | # 場所と p 値の表示 |
| } | # |
| showpt.f(pth$p.value, 0.05) | # 対比較ホルム補正で 5 %有意となった比較 |
| showpt.f(ptb$p.value, 0.05) | # 対比較ボンフェローニ補正で 5 %有意となった比較 |
| showpt.f(ptn$p.value, 0.05) | # 対比較補正なしで 5 %有意となった比較 |
| # 多重比較の計算を詳しくみる(品種1と5の比較) | |
| c15 <- c(1,0,0,0,-1,0,0,0,0) | # 対比ベクトル |
| mc15 <- c15 %*% c15 | # 大きさ |
| c15sd <- sqrt(mc15)*esd/sqrt(n) | # 対比較の標準誤差 |
| c15e <- t(c15) %*% gm | # 対比較推定値 |
| tv15 <- c15e/c15sd; tv15 | # 対比較 t 値 |
| pv15 <- 2*(1 - pt(abs(tv15), df=(nn-a)));pv15 | # 対比較 p 値 |
| k <- a*(a-1)/2 | # 比較の総数 |
| pv15*k | # 対比較 p 値ボンフェローニ補正 |
| hsd <- TukeyHSD(aov(y ~ x)); hsd | # チューキー HSD のすべての組み合わせの結果表示 |
| ph <- hsd$x[,4] | # 各比較の p 値ベクトル |
| sc <- (1:length(ph))[ph<0.05] | # p 値が 0.05 以下の比較 |
| hsd$x[sc,] | # 5 %有意な比較 |
| 多重比較法 | 共通の組み合わせ | 補正なしと HSD | 補正なし |
|---|---|---|---|
| ホルム補正 | 1-5 2-4 2-5 2-8 5-9 |
||
| ボンフェローニ補正 | |||
| 補正なし | 5-7 | 1-4 1-8 2-3 2-6 2-7 3-5 4-9 5-6 8-9 | |
| チューキー HSD |
その結果は以下の表のようになった.また,分散分析の F 検定で有意になったときと
そうでないときで多重比較で有意な組み合わせが見つかったかどうかも分類した.これをみると,
補正なしの多重比較は有意水準 25 %以上で,
明らかにゴーストを拾ってしまうことがわかり,これを使ってはいけないことが
示された.
一方,ホルム補正とボンフェローニ補正は,このシミュレーションでは違いがまったくなかった.
これは,p 値の最小値の補正はどちらも α/r であるからである.
有意水準が 4 %ぐらいであり,問題がないと言える.チューキー HSD の有意水準は約 5 %
で一番よいと言える.
また,分散分析 F 検定との関連をみると,多重比較の有意な組み合わせの有無は F 検定と
大きく関連があると言えるが,まったく一致しているわけではなかった.分散分析 F 検定と多重比較は
違う検定と考えた方がよいと思われる.すなわち,分散分析 F 検定が有意なときだけ多重比較を行うと
有意水準が低下するので,より保守的な検定になってしまうからである.
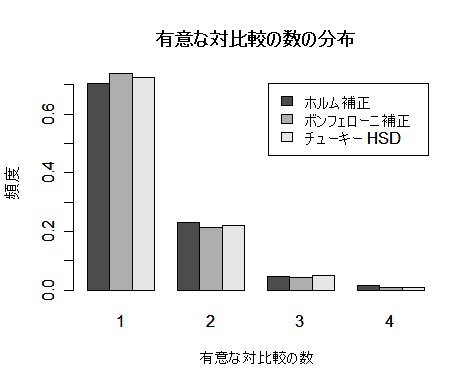
多重比較の方式による違いをより詳しくみるために,p 値の最小値が 0.05 以下であるときに 有意な対比較の個数の分布もみた.これをみると,ホルム補正,ボンフェローニ補正,チューキー HSD いずれも個数分布がよく似ていた.帰無仮説が真であるときは,ホルム補正とボンフェローニ補正では 違いがほとんどないと思われる.
| F 検定 | ホルム補正 | ボンフェローニ補正 | 補正なし | チューキー HSD | |
|---|---|---|---|---|---|
| 有意水準 | 0.0497 | 0.0377 | 0.0377 | 0.2807 | 0.0503 |
| 有意となった組み合わせ があった回数 | 有意なとき(497) | 337 | 337 | 497 | 393 |
| 有意でないとき | 40 | 40 | 2310 | 110 |
| N <- 100 | # シミュレーション回数(時間節約のため減らした) |
| a <- 5; n <- 10 | # 処理水準数 a,処理内標本数 n |
| x <- NULL | # |
| for(i in 1:a) x <- c(x, rep(i, n)) | # グループラベル |
| x <- factor(x) | # ラベル化 |
| pv <- NULL; sn <- NULL | # p 値行列と 5 %有意な個数 |
| for(i in 1:N){ | # |
| y <- rnorm(n*a) | # 標準正規乱数 n*a 個 |
| pth <- pairwise.t.test(y, x) | # 対比較ホルム補正 |
| ptb <- pairwise.t.test(y, x, p.adj = "bonf") | # 対比較ボンフェローニ補正 |
| ptn <- pairwise.t.test(y, x, p.adj = "none") | # 対比較補正なし |
| av <- aov(y ~ x) | # 分散分析 |
| hsd <- TukeyHSD(av) | # チューキー HSD |
| p0 <- summary(av)[[1]][1,5] | # 分散分析 p 値 |
| p1 <- min(pth$p.value, na.rm=TRUE) | # 対比較ホルム補正の p 値の最小値 |
| n1 <- length(which(pth$p.value < 0.05)) | # 対比較ホルム補正の 5 %有意の個数 |
| p2 <- min(ptb$p.value, na.rm=TRUE) | # 対比較ボンフェローニ補正の p 値の最小値 |
| n2 <- length(which(ptb$p.value < 0.05)) | # 対比較ボンフェローニ補正の 5 %有意の個数 |
| p3 <- min(ptn$p.value, na.rm=TRUE) | # 対比較補正なしの p 値の最小値 |
| n3 <- length(which(ptn$p.value < 0.05)) | # 対比較補正なしの 5 %有意の個数 |
| p4 <- min(hsd$x[,4]) | # チューキー HSD の p 値の最小値 |
| n4 <- length(which(hsd$x[,4] < 0.05)) | # チューキー HSD の 5 %有意の個数 |
| pv <- rbind(pv, c(p0, p1,p2,p3,p4)) | # p 値行列に格納 |
| sn <- rbind(sn, c(n1,n2,n3,n4)) | # 有意個数行列に格納 |
| } | # |
| fs <- (1:N)[pv[,1]<0.05] | # 分散分析で 5 %有意となった回の番号 |
| hs <- (1:N)[pv[,2]<0.05] | # 対比較ホルム補正で 5 %有意な組み合わせがあった回の番号 |
| bs <- (1:N)[pv[,3]<0.05] | # 対比較ボンフェローニ補正で 5 %有意な組み合わせがあった回の番号 |
| ns <- (1:N)[pv[,4]<0.05] | # 対比較補正なしで 5 %有意な組み合わせがあった回の番号 |
| ts <- (1:N)[pv[,5]<0.05] | # チューキー HSD で 5 %有意な組み合わせがあった回の番号 |
| num <- c(length(fs), length(hs), length(bs), length(ns), length(ts)) | |
| num/N | # 有意水準 |
| table(hs %in% fs) | # 対比較ホルム補正の番号と分散分析有意の番号とのマッチング |
| table(bs %in% fs) | # 対比較ボンフェローニ補正の番号と分散分析有意の番号とのマッチング |
| table(ns %in% fs) | # 対比較補正なしの番号と分散分析有意の番号とのマッチング |
| table(ts %in% fs) | # チューキー HSD の番号と分散分析有意の番号とのマッチング |
| ths <- table(sn[hs,1]); ths | # 対比較ホルム補正の有意な個数の分布 |
| tbs <- table(sn[bs,2]); tbs | # 対比較ボンフェローニ補正の有意な個数の分布 |
| tns <- table(sn[ns,3]); tns | # 対比較補正なしの有意な個数の分布 |
| tts <- table(sn[ts,4]); tts | # チューキー HSD の有意な個数の分布 |
| ths <- ths/sum(ths); tbs <- tbs/sum(tbs); tts <- tts/sum(tts) | |
| barplot(rbind(ths,tbs,tts), beside=TRUE, xlab="有意な対比較の数", ylab="頻度", legend=c("ホルム補正","ボンフェローニ補正", "チューキー HSD")) | |
| title(main="有意な対比較の数の分布") | # |
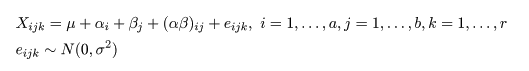
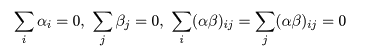
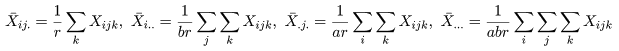
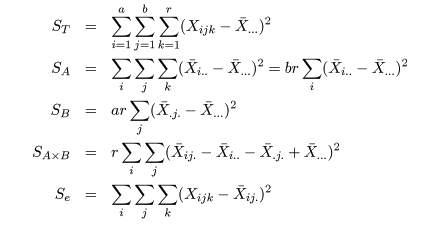
| 変動因 | 自由度(df) | 平方和(S.S.) | 平均平方(M.S.) | F 値 |
|---|---|---|---|---|
| 主効果 A | a - 1 | SA | MA = SA/(a - 1) | MA/Me |
| 主効果 B | b - 1 | SB | MB = SB/(b - 1) | MB/Me |
| 交互作用 | (a - 1)(b - 1) | SA×B | MA×B = SA×B/(a - 1)(b - 1) | MA×B/Me |
| 誤 差 | ab(r - 1) | Se | Me = Se/(n - a) | |
| 全 体 | n - 1 | ST |
| rice <- read.csv("ricecul.csv") | # コメデータ読み込み |
| rice[rice$year==2000,] | # 2000年度データの表示 |
| yield0 <- rice$gy[rice$year==2000] | # 2000年度収量 |
| dens0 <- factor(rice$density[rice$year==2000]) | # 2000年度密度水準のラベル化 |
| fert0 <- factor(rice$fert[rice$year==2000]) | # 2000年度肥料水準のラベル化 |
| blk0 <- factor(rice$rep[rice$year==2000]) | # 2000年度ブロックのラベル化 |
| cbind(yield0, dens0, fert0, blk0) | # データと変数の表示 |
| tapply(yield0, dens0, mean) | # 栽植密度水準ごとの収量平均 |
| tapply(yield0, fert0, mean) | # 施肥量水準ごとの収量平均 |
| x <- tapply(yield0, dens0:fert0, mean); x | # 栽植密度と施肥量組み合わせの収量平均 |
| ry.aov <- aov(yield0 ~ blk0 + dens0 + fert0 + dens0:fert0) | # 2要因乱塊法分散分析 |
| summary(ry.aov) | # 分散分析表表示 |
| plot(1:3, x[1:3], type="b", lwd=2, xaxt="n", xlab="施肥量", ylab="収量", ylim=c(300, 600), pch=0, col="blue") | |
| axis(1, 1:3, labels=c("施肥無","施肥少","施肥多")) | # グラフ表示 |
| points(1:3, x[4:6], type="b", lwd=2, pch=2, col="red") | # |
| legend(locator(1), legend=c("疎植","密植"), pch=c(0,2), col=c("blue","red")) | |
| title(main="栽植密度と施肥量の交互作用(2000年)") | # |
| yield <- rice$gy | # コメ収量データ |
| dens <- factor(rice$density) | # 密度水準のラベル化 |
| fert <- factor(rice$fert) | # 施肥量水準のラベル化 |
| year <- factor(rice$year) | # 年次のラベル化 |
| cbind(yield, dens, fert, year) | # データと変数の表示 |
| rya.aov <- aov(yield ~ dens + fert + year + dens:fert + fert:year + dens:year + dens:fert:year) | |
| summary(rya.aov) | # 3元配置分散分析表 |
| x <- tapply(rice$gy, fert:year, mean) | # 年次と施肥量組み合わせの収量平均 |
| plot(1:4, x[1:4], type="b", lwd=2, xaxt="n", xlab="年次", ylab="収量", ylim=c(300,600), pch=0, lty=1,col="red") | |
| axis(1, 1:4, labels=levels(year)) | # グラフ表示 |
| points(1:4, x[5:8], type="b", lwd=2, pch=2,lty=1, col="blue") | # |
| points(1:4, x[9:12], type="b", lwd=2, pch=3,lty=1, col="green") | # |
| legend(locator(1), legend=c("施肥無","施肥少","施肥多"), pch=c(0,2,3), col=c("red","blue","green")) | |
| title(main="年次と施肥量の交互作用") | # |
標本(サンプル)に対し,2つの変数 x,y が測定されているとする. たとえば,x が身長(m)であり,y が体重(kg)である. 大きさ n の標本(サンプル)に対し,2つの変数の組のデータが,
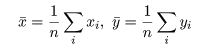
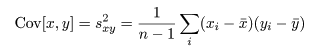
共分散は測定単位により大きさが変わるので,これをおのおのの変数の標本分散, Var[x],Var[y],
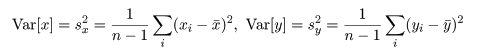
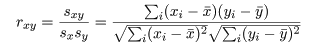
 |
 |
 |
 |
| r <- read.csv("r1.csv") | # csv データ読み込み |
| x <- r[,1]; y <- r[,2] | # |
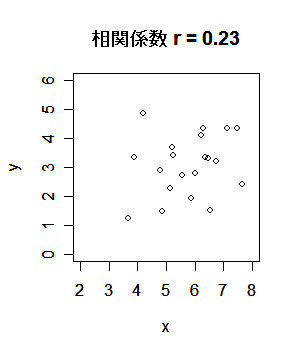
| plot(x,y, xlim=c(2,8), ylim=c(0,6)) | # x,y の散布図 |
| title(main="相関係数 r = 0.23") | # |
| cov(x, y) | # x と y の共分散 |
| cor(x, y) | # x と y の相関係数 |
| x <- 10*x | # |
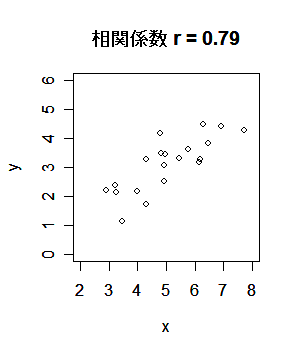
| plot(x,y, xlim=c(2,8), ylim=c(0,6)) | # x,y の散布図 |
| cov(x, y) | # x と y の共分散 |
| cor(x, y) | # x と y の相関係数 |
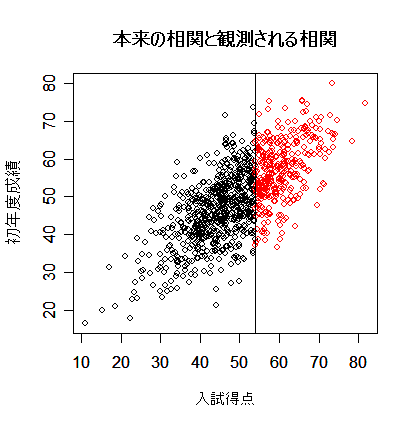
| library(MASS) | # MASS ライブラリーの読み込み |
| s <- matrix(c(100, 70, 70, 100), nrow=2) | # 分散共分散行列の定義 |
| x <- mvrnorm(1000,c(50,50),s) | # 平均 50,分散 s の 2 変量正規分布乱数 1000 個生成 |
| plot(x, xlab="入試得点", ylab="初年度成績") | # 分布全体を表示 |
| points(x[x[,1]>54,], col="red") | # 入学者のみ赤で表示 |
| abline(v=54) | # 合格ライン |
| title(main="本来の相関と観測される相関") | # |
| cor(x)[1,2] | # 本来あるべき相関 |
| cor(x[x[,1]>54,])[1,2] | # 実際に観測される相関 |
データに最もよくあてはまる直線回帰式を得るには,データ点 (xi ,yi ), と回帰による推定点, (xi ,y^i ), y^i = a + b xi , の間の距離の2乗和 S が最小になるような回帰係数 a ,b を求める.つまり,
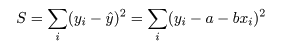
これは,S を a ,b で偏微分して 0 とおくことによって得られる.つまり,
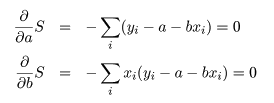
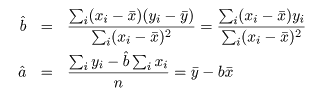
| 入試得点(x) | 680 | 500 | 600 | 420 | 480 | 630 | 550 | 590 | 610 | 500 | 640 | 570 | 610 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 初年度成績(y) | 332 | 265 | 309 | 253 | 276 | 326 | 299 | 310 | 324 | 327 | 334 | 301 | 336 |
mba <- read.csv("mbagrade.csv"); mba # データ読み込み
mbaf <- mba[mba[,1]=="F",] ; mbaf # 女子のみのデータ
mbaf.lm <- lm(Grade1st ~ Entexam, data=mbaf) # 回帰:lm(y ~ x, data=zzz), y = ax + b
summary(mbaf.lm) # 結果表示
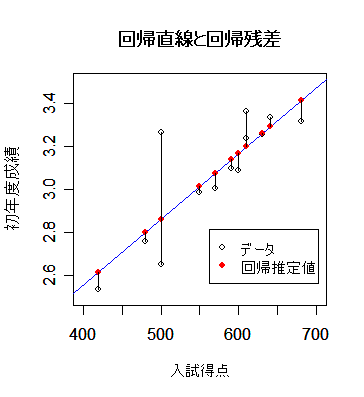
plot(mbaf[,2:3], xlim=c(400,700), ylim=c(2.5,3.5), xlab="入試得点", ylab="初年度成績") # データ散布図
abline(mbaf.lm, col="blue") # 回帰直線表示
points(mbaf[,2], fitted(mbaf.lm), pch=19, col="red") # 回帰推定値
segments(mbaf[,2],mbaf[,3],mbaf[,2], fitted(mbaf.lm)) # 回帰残差
title(main="回帰直線と回帰残差") #
legend(locator(1), legend=c("データ","回帰推定値"), pch=c(1,19), col=c("black","red"))
|
推定された直線回帰式がどの程度現実のデータに適合しているかを調べるために, 回帰式が従う統計モデルを考える.標本の格データ点, (xi ,yi ), が,
回帰で説明がつかない残差平方和 Se は,
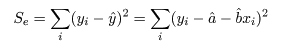
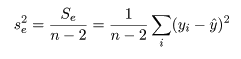
一般に,Var(yi ) = σ2 であるとき,その定数(c) 倍の分散は,
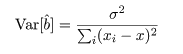
目的変数 y が説明変数 x との回帰関係にないという 帰無仮説,
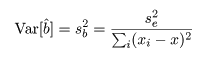
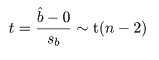
回帰式により, 従属変数 y のデータ yi は,
データが直線回帰式でよく説明できるのは,回帰平方和が大きく,残差平方和 が小さい場合である.総平方和のうち回帰平方和で説明される割合を決定係数,もしくは 重相関係数の2乗といい,
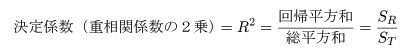
| 変動因 | 平方和 | 自由度 | 平均平方 | F 値 |
|---|---|---|---|---|
| 回帰 | SR | 1 | SR | F = SR/se2 |
| 残差 | Se | n−2 | se2 = Se/n−2 | |
| 全体 | ST | n−1 |
従属変数 y が説明変数 x の回帰関係にないという 帰無仮説,
anova(mbaf.lm) # 分散分析表 n <- nrow(mbaf); n # データ数 st <- var(mbaf[,3])*(n-1); st # 総平方和 sr <- var(fitted(mbaf.lm))*(n-1); sr # 回帰平方和 se <- var(resid(mbaf.lm))*(n-1); se # 残差平方和 s <- sqrt(se/(n-2)); s # 残差標準偏差 sx <- var(mbaf[,2])*(n-1); sx # x の総平方和 b <- cov(mbaf[,2],mbaf[,3])*(n-1)/sx; b # 回帰係数 sb <- s/sqrt(sx); sb # 回帰係数bの標準誤差 r2 <- sr/st; r2 # 重相関係数の2乗 r <- cor(mbaf[,3], fitted(mbaf.lm)); r # 目的変数と回帰推定値の相関 fv <- sr/(se/(n-2)); fv # F値 tv <- b/sb; tv # t値 |
回帰係数の標準誤差 s b を用いて, 回帰係数 b の信頼区間がつくれる.すなわち, 自由度 n−2 の t 分布の 97.5%点を t0 とすると, 回帰係数 b の 95%信頼区間の幅 d は,d = t0 s b となるので, 95%信頼区間は,
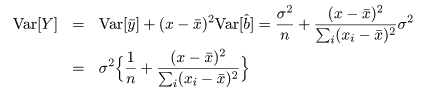
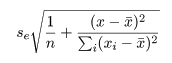
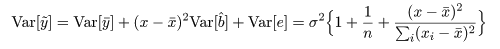
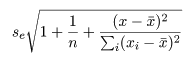
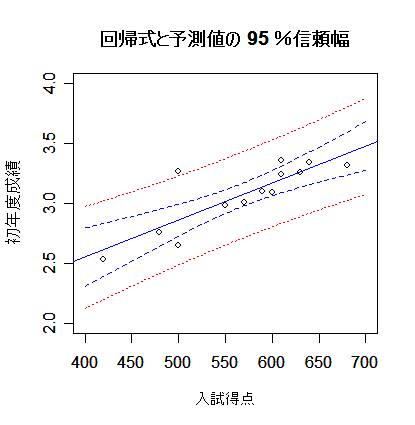
new <- data.frame(Entexam=seq(400,700,by=2)) # 予測したい範囲の定義
Grac <- predict(mbaf.lm, new, interval="confidence", level=0.95) # 回帰推定値(回帰直線)の 95 %信頼幅
Grap <- predict(mbaf.lm, new, interval="prediction", level=0.95) # 回帰予測値の 95 %信頼幅
matplot(new$Entexam, cbind(Grac,Grap[,-1]), lty=c(1,2,2,3,3), type="l",
col=c("blue","blue","blue","red","red"), xlab="入試得点", ylab="初年度成績")
points(mbaf[,2:3]) # データの表示
title(main="回帰式と予測値の 95 %信頼幅") #
|
| # 信頼幅を詳しく計算 |
n <- nrow(mbaf); n # データ数 sx <- var(mbaf$Entexam)*(n-1); sx # x の偏差平方和 se <- summary(mbaf.lm)$sigma; se # 残差標準偏差 b <- coef(mbaf.lm)[2]; b # 回帰係数 mx <- mean(mbaf$Entexam) # x の平均 my <- mean(mbaf$Grade1st) # y の平均 t0 <- qt(0.975, df=(n-2)); t0 # 自由度 n - 2 の t 分布 97.5%点 x11() # 新しいグラフウィンドウで表示 plot(mbaf[,2:3], xlim=c(400,700), ylim=c(2,4)) # データ散布図 abline(mbaf.lm, col="blue") # 回帰直線 sr <- 1/n + (new$Entexam-mx)^2/sx # y1 <- my + b*(new$Entexam-mx) + t0*se*sqrt(sr) # 回帰直線 95%信頼幅上限 y2 <- my + b*(new$Entexam-mx) - t0*se*sqrt(sr) # 回帰直線 95%信頼幅下限 points(new$Entexam, y1, type="l", lty=2, col="blue") # points(new$Entexam, y2, type="l", lty=2, col="blue") # yp1 <- my + b*(new$Entexam-mx) + t0*se*sqrt(sr+1) # 回帰予測値 95%信頼幅上限 yp2 <- my + b*(new$Entexam-mx) - t0*se*sqrt(sr+1) # 回帰予測値 95%信頼幅下限 points(new$Entexam, yp1, type="l", lty=3, col="red") # points(new$Entexam, yp2, type="l", lty=3, col="red") # title(main="回帰式と予測値の 95 %信頼幅") |
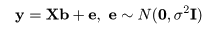
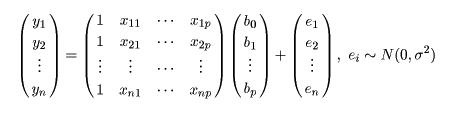
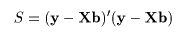
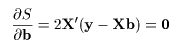
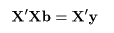
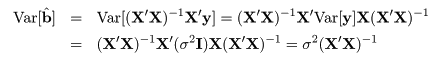
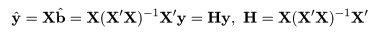
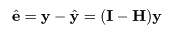
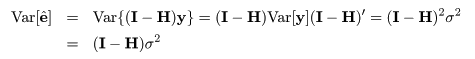
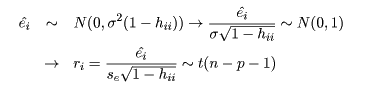
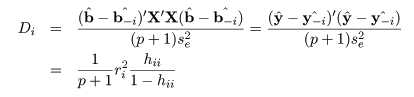
 |
 |
 |
 |
mba <- read.csv("mbagrade.csv") # データ読み込み
mbaf <- mba[mba[,1]=="F",] # 女性データのみ抽出
mbaf.lm <- lm(Grade1st ~ Entexam, data=mbaf) # 回帰
summary(mbaf.lm) # 結果表示
plot(mbaf.lm) # 回帰診断はたったこれだけ.(4枚のグラフが出てくる)
#
# 回帰診断を詳しくみる
# てこ比
lev <- hatvalues(mbaf.lm); lev # てこ比
X <- model.matrix(mbaf.lm) # 説明変数行列
H <- X %*% solve(t(X) %*% X) %*% t(X) # ハット行列
diag(H) # てこ比の計算による導出
# 標準化残差
rstd <- rstandard(mbaf.lm); rstd # 標準化残差
se <- summary(mbaf.lm)$sigma # 残差標準偏差
resid(mbaf.lm)/(se*sqrt(1-lev)) # 標準化残差の計算による導出
# Cook 距離
cookd <- cooks.distance(mbaf.lm); cookd # Cook 距離
b <- coef(mbaf.lm); b # 回帰係数
lm1 <- lm(Grade1st[-1] ~ Entexam[-1], data=mbaf)
b1 <- coef(lm1); b1 # 1番目のデータを除いた回帰係数
t(b-b1) %*% t(X) %*% X %*% (b-b1)/se^2/2 # 1番目のデータの Cook 距離
rstd^2*lev/(1-lev)/2 # Cook 距離の計算による導出
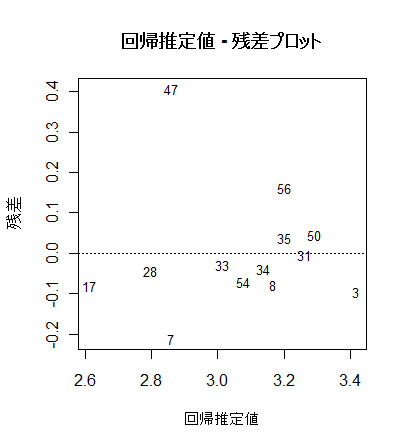
# 回帰推定値 - 残差プロット
x0 <- fitted(mbaf.lm) # 回帰推定値
y0 <- resid(mbaf.lm) # 回帰残差
plot(x0, y0, type="n", xlab="回帰推定値", ylab="残差") #
text(x0, y0, rownames(mbaf), cex=0.8)
abline(h=0, lty=3)
title(main="回帰推定値 - 残差プロット")
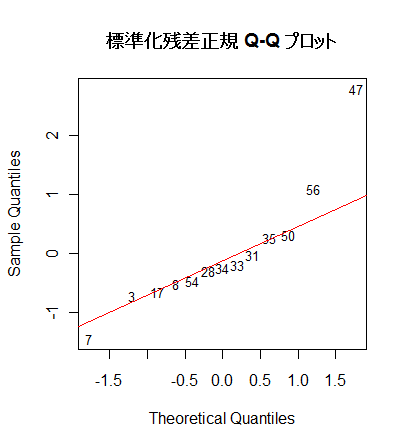
# 標準化残差 Q - Q プロット
a <- qqnorm(rstd, type="n", main="") # 標準化残差の Q - Q プロット(正規分布からのずれ)
text(a, rownames(mbaf), cex=0.8)
qqline(rstd, col="red")
title("標準化残差正規 Q-Q プロット")
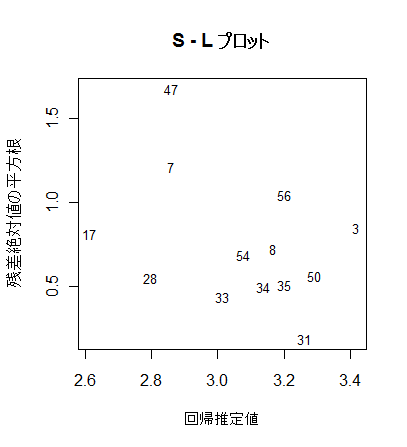
# S - L プロット
yr <- sqrt(abs(rstd)) # 標準化残差絶対値の平方根
plot(x0, yr, type="n", xlab="回帰推定値", ylab="残差絶対値の平方根") #
text(x0, yr, rownames(mbaf), cex=0.8)
title(main="S - L プロット")
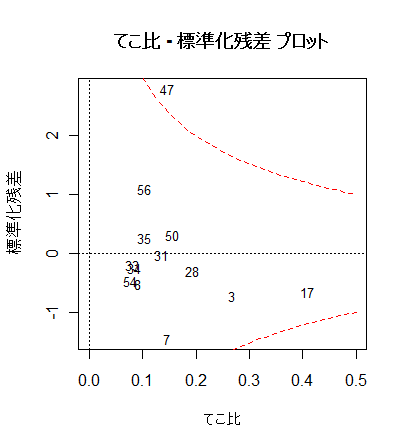
# てこ比 - 標準化残差 プロット
plot(lev, rstd, type="n", xlim=c(0,0.5), xlab="てこ比", ylab="標準化残差")
text(lev, rstd, rownames(mbaf), cex=0.8)
abline(h=0, lty=3)
abline(v=0, lty=3)
title(main="てこ比 - 標準化残差 プロット")
xx <- seq(0, 0.5, by=0.01)
yc <- .5*2*(1-xx)/xx # Cook 距離 0.5 となる標準化残差
yc1 <- sqrt(yc)
yc2 <- -yc1
points(xx, yc1, type="l", lty=2, col="red") # Cook 距離 0.5 線
points(xx, -yc1, type="l", lty=2, col="red")
|
mba <- read.csv("mbagrade.csv") # データ読み込み
nf <- which(mba[,1]=="F") # 女子データの番号
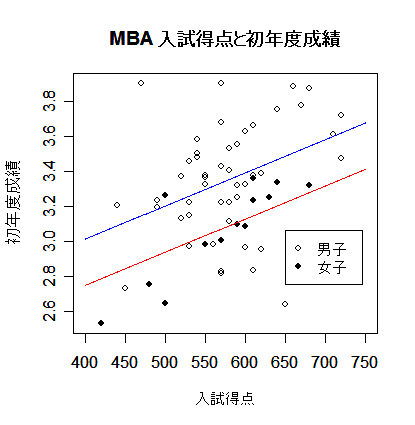
mba.lm <- lm(Grade1st ~ Sex + Entexam, data=mba) # 重回帰分析
summary(mba.lm) # 結果表示
anova(mba.lm) # 分散分析表示
#
# グラフ表示
plot(mba[,2:3], type="n", xlim=c(400,750), xlab="入試得点", ylab="初年度成績") #
points(mba[-nf,2:3], pch=21) # 男子データ(白丸)
points(mba[nf,2:3], pch=19) # 女子データ(黒丸)
b <- coef(mba.lm) # 回帰係数
x <- seq(400,750,by=1) #
ym <- b[1] + b[2] + b[3]*x # 男子回帰式
yf <- b[1] + b[3]*x # 女子回帰式
lines(x, ym, type="l", col="blue") #
lines(x, yf, type="l", col="red") #
legend(locator(1), c("男子","女子"), pch=c(21,19)) #
title(main="MBA 入試得点と初年度成績") #
|
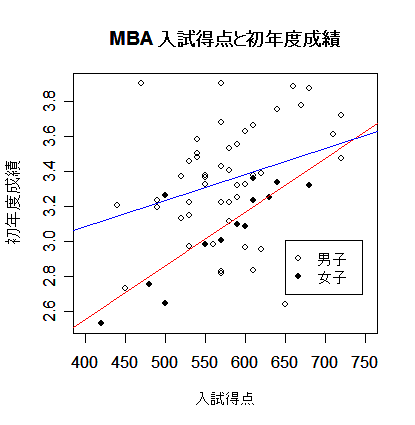
| mba2.lm <- lm(Grade1st ~ Sex + Sex:Entexam, data=mba) # 重回帰分析 summary(mba2.lm) # 結果表示 anova(mba2.lm) # plot(mba[,2:3], type="n", xlim=c(400,750), xlab="入試得点", ylab="初年度成績") # points(mba[-nf,2:3], pch=21) # 男子データ(白丸) points(mba[nf,2:3], pch=19) # 女子データ(黒丸) b <- coef(mba2.lm) # 回帰係数 x <- seq(400,750,by=1) # ym <- b[1] + b[2] + b[4]*x # 男子回帰式 yf <- b[1] + b[3]*x # 女子回帰式 lines(x, ym, type="l", col="blue") # lines(x, yf, type="l", col="red") # legend(locator(1), c("男子","女子"), pch=c(21,19)) # title(main="MBA 入試得点と初年度成績") # # |
k 個のパラメータ θ を持つ回帰モデル
| anova(mba.lm) | # 性別,入試得点重回帰の分散分析表 |
| AIC(mba.lm) | # 性別,入試得点重回帰モデルの AIC |
| n <- nrow(mba) | # 総データ数 |
| v2 <- anova(mba.lm)[3,2]/n | # 残差分散の最尤推定値(n で割る) |
| aic <- n*log(2*pi) + n*log(v2) + n + 2*4; aic | # 自由パラメータ数 4 の AIC |
| anova(mba2.lm) | # 男女別々回帰,残差分散共通の分散分析表 |
| AIC(mba.lm) | # 男女別々回帰,残差分散共通モデルの AIC |
| anova(mbaf.lm) | # 男子単回帰分散分析表 |
| anova(mbam.lm) | # 女子単回帰分散分析表 |
| AIC(mbaf.lm)+AIC(mbam.lm) | # 男女完全別々モデルの AIC |
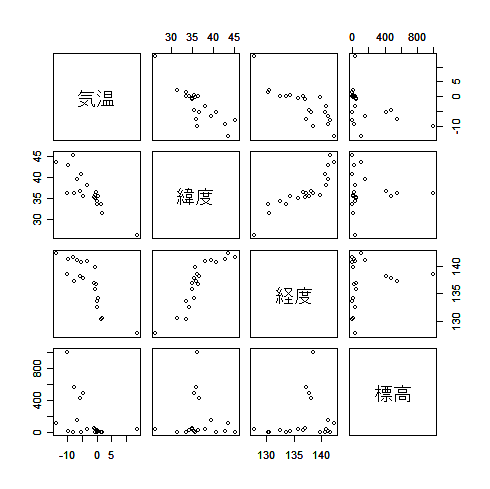
| kion <- read.csv("kion.csv") | # 気温データ読み込み |
| pairs(kion[,2:5]) | # 変数間散布図一覧 |
| cor(kion[,2:5]) | # 変数間相関 |
| kion1.lm <- lm(気温 ~ 緯度 + 経度 + 標高, data=kion) | # 3 変数重回帰 |
| summary(kion1.lm) | # 結果表示 |
| anova(kion1.lm) | # 分散分析表示 |
| n <- nrow(kion) | # データ数 |
| x0 <- rep(1,n) | # |
| x <- as.matrix(cbind(x0, kion[,3:5])) | # 説明変数行列 |
| se2 <- anova(kion1.lm)[4,3] | # 残差分散 |
| v <- se2 * solve(t(x) %*% x) | # 回帰係数の分散共分散行列 |
| sqrt(diag(v)) | # 回帰係数の標準誤差 |
| kion0.lm <- lm(気温 ~ 1, data=kion) | # 説明変数無し回帰 |
| anova(kion0.lm) | # |
| kion11.lm <- lm(気温 ~ 緯度, data=kion) | # 説明変数:緯度,回帰 |
| anova(kion11.lm) | # |
| kion12.lm <- lm(気温 ~ 経度, data=kion) | # 説明変数:経度,回帰 |
| anova(kion12.lm) | # |
| kion13.lm <- lm(気温 ~ 標高, data=kion) | # 説明変数:標高,回帰 |
| anova(kion13.lm) | # |
| kion21.lm <- lm(気温 ~ 緯度 + 経度, data=kion) | # 説明変数:緯度,経度,回帰 |
| anova(kion21.lm) | # |
| kion22.lm <- lm(気温 ~ 経度 + 標高, data=kion) | # 説明変数:経度,標高,回帰 |
| anova(kion22.lm) | # |
| kion23.lm <- lm(気温 ~ 緯度 + 標高, data=kion) | # 説明変数:緯度,標高,回帰 |
| anova(kion23.lm) | # |
| kion3.lm <- lm(気温 ~ 緯度 + 経度 + 標高, data=kion) | # 説明変数:緯度,経度,標高,回帰 |
| anova(kion3.lm) | # |
| AIC(kion0.lm) | # 説明変数無し回帰 AIC |
| AIC(kion11.lm) | # 説明変数:緯度,回帰 AIC |
| AIC(kion12.lm) | # 説明変数:経度,回帰 AIC |
| AIC(kion13.lm) | # 説明変数:標高,回帰 AIC |
| AIC(kion21.lm) | # 説明変数:緯度,経度,回帰 AIC |
| AIC(kion22.lm) | # 説明変数:経度,標高,回帰 AIC |
| AIC(kion23.lm) | # 説明変数:緯度,標高,回帰 AIC |
| AIC(kion3.lm) | # 説明変数:緯度,経度,標高,回帰 AIC |
| library(MASS) | # MASS ライブラリィー読み込み |
| null <- lm(気温 ~ 1, kion) | # 説明変数無し |
| full <- lm(気温 ~ 緯度 + 経度 + 標高, kion) | # 説明変数3つ |
| result <- stepAIC(null, scope=list(lower=null, upper=full), data=kion) | # 変数増減法 |
| summary(result) | # 結果表示 |
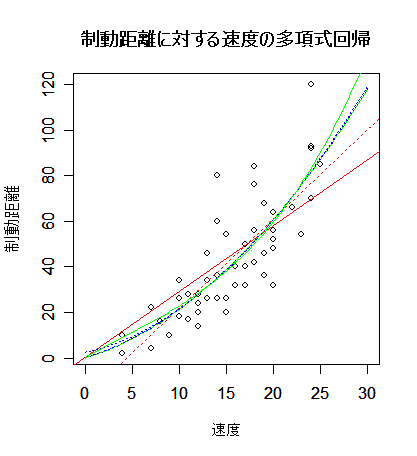
| cars | # R 付属データ 'cars' の呼び出し |
| plot(cars, xlim=c(0,30), xlab="速度", ylab="制動距離") | # cars の散布図 |
| title(main="制動距離に対する速度の多項式回帰") | # |
| y <- cars$dist | # 目的変数(制動距離) |
| x <- cars$speed | # 説明変数(速度) |
| car1.lm <- lm(y ~ x) | # 1次回帰 |
| abline(car1.lm, lty=3, col="red") | # 赤点線で表示 |
| summary(car1.lm) | # |
| car10.lm <- lm(y ~ 0 + x) | # 原点を通る1次回帰 |
| abline(car10.lm, col="red") | # 赤実線で表示 |
| summary(car10.lm) | # |
| x2 <- x^2 | # x の2乗を新しい変数で定義 |
| car2.lm <- lm(y ~ x + x2) | # 重回帰(2次式回帰) |
| b <- car2.lm$coefficients | # 回帰係数 |
| xv <- seq(0, 30, by=0.2) | # x の点列の定義 |
| yv <- b[1] + b[2]*xv + b[3]*xv^2 | # x の点列に対する2次回帰推定値 |
| lines(xv, yv, lty=3, col="blue") | # 青点線で表示 |
| summary(car2.lm) | # |
| car20.lm <- lm(y ~ 0 + x + x2) | # 原点を通る2次式回帰 |
| b <- car20.lm$coefficients | # 回帰係数 |
| yv <- b[1]*xv + b[2]*xv^2 | # x の点列に対する2次回帰推定値 |
| lines(xv, yv, col="blue") | # 青実線で表示 |
| summary(car20.lm) | # |
| x3 <- x^3 | # x の3乗を新しい変数で定義 |
| car3.lm <- lm(y ~ x + x2 + x3) | # 3変数重回帰(3次式回帰) |
| b <- car3.lm$coefficients | # 回帰係数 |
| yv <- b[1] + b[2]*xv + b[3]*xv^2 + b[4]*xv^3 | # x の点列に対する3次回帰推定値 |
| lines(xv, yv, lty=3, col="green") | # 緑点線で表示 |
| summary(car3.lm) | # |
| car30.lm <- lm(y ~ 0 + x + x2 + x3) | # |
| b <- car30.lm$coefficients | # 回帰係数 |
| yv <- b[1]*xv + b[2]*xv^2 + b[3]*xv^3 | # x の点列に対する3次回帰推定値 |
| lines(xv, yv, col="green") | # 緑実線で表示 |
| summary(car30.lm) | # |
| AIC(car1.lm) | # 1次回帰の AIC |
| AIC(car10.lm) | # 原点を通る1次回帰の AIC |
| AIC(car2.lm) | # 2次式回帰の AIC |
| AIC(car20.lm) | # 原点を通る2次式回帰の AIC |
| AIC(car3.lm) | # 3次式回帰の AIC |
| AIC(car30.lm) | # 原点を通る3次式回帰の AIC |
| cars | # R 付属データ 'cars' の呼び出し |
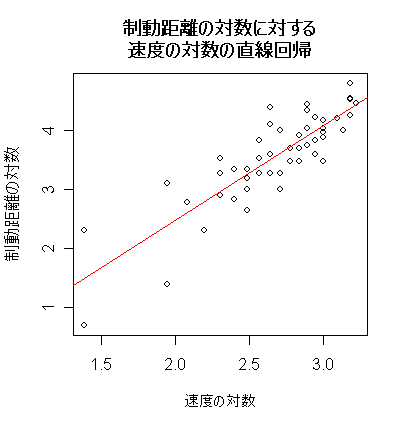
| y <- log(cars$dist) | # 目的変数(制動距離)の対数 |
| x <- log(cars$speed) | # 説明変数(速度)の対数 |
| plot(x, y, xlab="速度の対数", ylab="制動距離の対数") | # cars の散布図 |
| title(main="制動距離の対数に対する\n速度の対数の直線回帰") | # |
| car.lm <- lm(y ~ x) | # 1次回帰 |
| abline(car.lm, col="red") | # 赤線で表示 |
| summary(car.lm) | # |
| n <- length(y) | #データ数(サンプルサイズ) |
| nx <- sample(1:n, replace=TRUE) | #B1:ブートストラップサンプル |
| cb.lm <- lm(y[nx] ~ x[nx]) | #B2 |
| plot(x[nx], y[nx], xlab="速度の対数", ylab="制動距離の対数") | # cars の散布図 |
| title(main="ブートストラップサンプルの直線回帰") | # |
| abline(cb.lm, col="red") | # 赤線で表示 |
| M <- 1000 | #ブートストラップの回数 |
| coeff.vec <- numeric(M) | #長さ M の 0 ベクトル |
| for(i in 1:M){ # { } 内 M 回繰り返し | |
| nx <- sample(1:n, replace=TRUE) | |
| coeff.vec[i] <- (lm(y[nx] ~ x[nx]))$coefficients[2] | |
| } | |
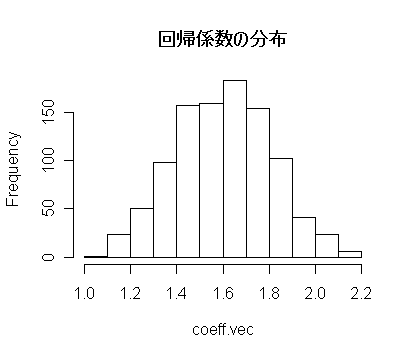
| hist(coeff.vec, main="回帰係数の分布") | #ブートストラップ回帰係数のヒストグラム |
| ord <- order(coeff.vec) | #回帰係数の順序 |
| LB1 <- coeff.vec[ord][25] | #下側2.5%点の推定値 |
| LB2 <- coeff.vec[ord][975] | #上側97.5%点の推定値 |
| cat("L1 = ", LB1, ", L2 = ",LB2 ,", delta = ", LB2-LB1,"\n") | #ブートストラップによる95%信頼区間 |
成長段階の異なる 47 頭のミヤマクワガタのパーツ別の重量データ(g).パーツは, 頭部(WHEAD),前胸部(WTHORAX),中胸〜腹部(WABDOM),交尾器(WGENI)からなる.
形態形質 x,y に対して,初期成長指数を a,成長比を b と したときの生物形態の相対成長式,