統計特論1
東京大学大学院農学生命科学研究科 大森宏
この講義の目的
統計解析ソフトRを用いて,統計解析が自在に行えるスキルを身に着ける.また,解析的証明より,
シミュレーションによる数値的な証明(厳密ではないが直感的に理解しやすい)を行い,統計学の
視覚的で直感的な理解をめざす.
Rの基本的使い方を学ぶ.
今日のスクリプト
| x <- c(2, 3, 5) | | #ベクトルの定義 |
| y <- c(10, 14, -7) | | |
| a <- matrix(1:9, nrow=3) | | #行列の定義 |
| b <- x %*% t(x) | | #行列の積 |
| z <- c(6, -5, 2) | | |
| a1 <- cbind(x,y,z) | | #列ベクトル->行列生成 |
| solve(a1) | | #逆行列 |
| eigen(a1) | | #固有値 |
| x <- 1:10 | | #連続した自然数 |
| y <- c(3,7,8,6,9,10,6,5,10,7) | | |
| plot(x, y) | | #散布図 |
| plot(x, y, type="l") | | #直線でつなぐ |
| x <-seq(-20, 20, by=0.1) | | #等間隔点列 |
| y <- x^2 | | #関数定義 |
| y <- 3*x^3 - 2*x^2 + 6*x + 5 | | |
| y <- -2*cos(x)+4*sin(x) | | |
| plot(x, y, type="l") | | #関数のグラフ |
| plot(x, y, type="l", xlim=c(-20,20), ylim=c(-20,20)) | | #表示部分の指定 |
0.R でできる関数解析
ニュートン法
Rでは,ニュートン法により方程式の根を求めることができる.
|
R による方程式の解法のスクリプト
# 関数の作成
f1 <- function(x){
exp(x)-2
}
#関数のグラフ
x <- seq(-1, 2, by=0.01)
plot(x, f1(x), type="l")
# これでもよい
curve(f1(x), -1,2)
#水平線と垂直線
abline(h=0)
abline(v=0)
#グラフタイトル
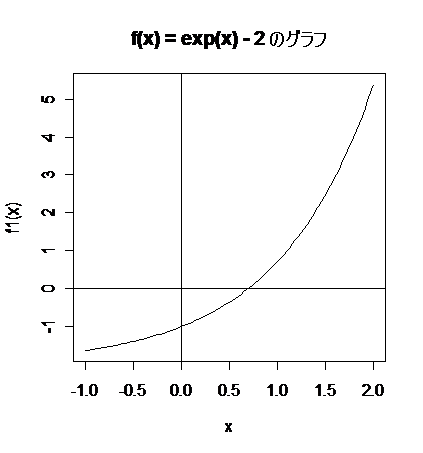
title(main="f(x) = exp(x) - 2 のグラフ")
# 0 < x < 1 で根を探す
uniroot(f1, c(0,1))
|
|
方程式,exp(x) - 2 = 0,の根は,x = log(2) = 0.6931472,で,ニュートン法による近似解は,
x = 0.6931457,であり,四捨五入した値で比較すると,小数第4位まで正確であった.
ニュートン法の R の出力
|
> uniroot(f1, c(0,1)) | | #根を探すコマンド |
|
$root | | |
|
[1] 0.6931457 | | 方程式の根 |
|
$f.root | | |
|
[1] -2.943424e-06 | | |
|
$iter | | |
|
[1] 5 | | ニュートン法の反復回数 |
|
$estim.prec | | 根の有効数字 |
|
[1] 6.103516e-05 | | 正確さの桁数は小数点4位まで |
|
> log(2) | | #Rのコマンド |
|
[1] 0.6931472 | | 正確な根 |
|
多項式方程式の根
# R による方程式の解法のスクリプト
# 2次方程式
# (x + 1)(x + 2) = 2 + 3x + x^2 = 0 の根
polyroot(c(2, 3, 1))
# 3次関数のグラフ
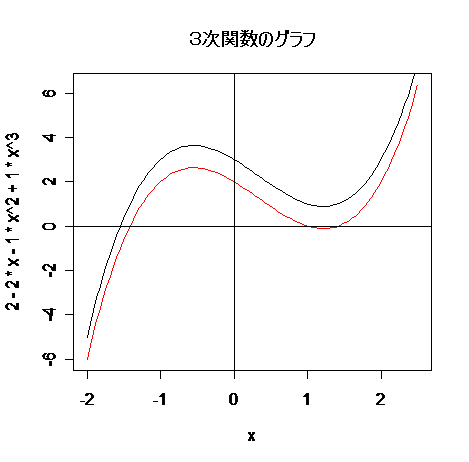
# f(x) = x3 - x2 - 2x + 2,のグラフ(赤色)
curve(2 - 2*x - 1*x^2 + 1*x^3, -2, 2.5, col="red")
# f(x) = x3 - x2 - 2x + 3,のグラフ(黒色)の重ね書き
curve(3 - 2*x - x^2 + x^3, -2, 2.5, add=TRUE)
#水平線と垂直線
abline(h=0)
abline(v=0)
title(main="3次関数のグラフ")
# 3次方程式
# (x^2 - 2)(x - 1) = 2 - 2*x - 1*x^2 + 1*x^3 = 0
# 3つの実数根
polyroot(c(2, -2, -1, 1))
# 3 - 2*x - 1*x^2 + 1*x^3 = 0
# 虚数解もでる.
polyroot(c(3, -2, -1, 1))
|
|
|
多項式方程式の R の出力
|
> polyroot(c(2, 3, 1)) | |
# 2 + 3x + x^2 = 0 の根 |
|
[1] -1+0i -2-0i | |
"0i" なので,実数解,x = -1,-2 である. |
|
> polyroot(c(2, -2, -1, 1)) | |
# 2 - 2*x - 1*x^2 + 1*x^3 = 0,の根 |
|
[1] 1.000000-0i -1.414214+0i 1.414214+0i
|
| |
"0i" なので,実数解,x = 1, -1.414214(≒-√2),1.414214,である. |
|
> polyroot(c(3, -2, -1, 1)) | |
# 3 - 2*x - 1*x^2 + 1*x^3 = 0,の根 |
|
[1] 1.273409+0.563821i -1.546818-0.000000i 1.273409-0.563821i |
| |
実数解:x = -1.546818,虚数解:x = 1.273409 ± 0.563821i |
|
最大最小
R では,関数の最大最小を求めることができる.
|
# R による最大最小問題のスクリプト
# 関数定義
f2 <- function(x){
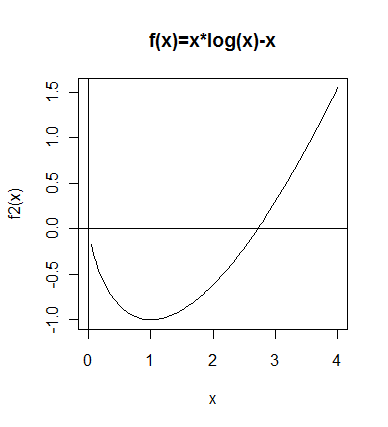
x*log(x)-x
}
# グラフ表示
curve(f2(x),0,4)
abline(h=0)
abline(v=0)
# 最大最小を探索する関数
optimize(f2, c(0.1, 2), maximum=F)
# 探索範囲(0.1 < x < 2),
# 最大値(maximum=T),最小値(maximum=F)
最大最小 R の出力
$minimum # 最小となる x
[1] 1.000019
$objective # 最小値
[1] -1
|
|
|
1.確率分布
離散確率分布
ある量の集まり 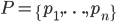 の中で,
の中で,
という性質をもつものを離散(discrete)確率分布(probability distribution)という.
各 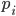 を確率密度(probability density)という.なお,
を確率密度(probability density)という.なお,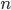 は可算無限(自然数と対応づけられる)であるならば離散的である.
は可算無限(自然数と対応づけられる)であるならば離散的である.
離散確率変数
離散的な変数 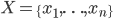 のおのおのの値に対し,それが生起する確率
のおのおのの値に対し,それが生起する確率 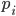 が与えられているとき,
が与えられているとき,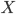 を離散確率変数(discrete random variable)という.これは,
を離散確率変数(discrete random variable)という.これは,
表 1 :離散確率変数(n = 5)
|
変数 X
|
x1
|
x2
|
x3
|
x4
|
x5
|
|
確率 P
|
p1
|
p2
|
p3
|
p4
|
p5
|
と表せる.
連続型確率分布
関数 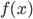 が,
が,
という性質を持つとき,これを連続型確率分布(continuous distribution)という.また,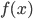 を確率密度関数(probability density function)とも呼ぶ.なお,確率密度関数
を確率密度関数(probability density function)とも呼ぶ.なお,確率密度関数 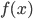 が,パラメータ
が,パラメータ 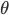 を持つとき,
を持つとき,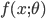 と表記することもある.
と表記することもある.
連続型確率変数
連続な変数 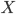 が分布
が分布 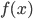 をもつとき,連続型確率変数(continuous random variable)もしくは変量(variate)という.本稿では,
をもつとき,連続型確率変数(continuous random variable)もしくは変量(variate)という.本稿では,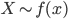 ,と表記する.
,と表記する.
累積分布関数
Pr[A] を事象 A が生起する確率とする.連続型確率変数 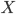 に対し,
に対し,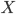 が
が 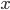 以下である確率,
以下である確率,
で定義される関数 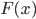 を累積分布関数(cumulative distribution function)という.この関数を用いると,確率変数
を累積分布関数(cumulative distribution function)という.この関数を用いると,確率変数 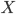 が区間
が区間 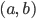 に落ちる確率は,
に落ちる確率は,
で表せる.なお,離散型確率変数でも積分を和に変えることにより,同様に階段型の累積分布関数が定義できる.
2.分布の代表値
平均
平均(mean)μ は,分布の中心的な位置(location)座標を表す.確率変数
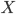
に対しては,
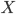
の期待値(expectation) E[
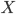
] とも表記し,
![\mu={\rm E}[X] = \int xf(x) dx \ \bigl(=\sum_ix_ip_i \bigr)](images/EXTERN_0017.png)
と定義される.離散確率変数では,積分を総和に変えることにより括弧内のように定義できる.
分散
分散(variance)
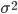
は,分布の拡がり(dispersion)の程度を表す.確率変数
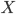
に対しては,Var[
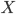
] と表記する.確率変数
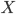
の関数
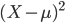
の期待値でもあり,
![\sigma^2 = {\rm Var}[X] ={\rm E}[(X-{\rm E}[X])^2] ={\rm E}[X^2] -({\rm E}[X])^2](images/EXTERN_0020.png)
![= {\rm E}[(X-\mu)^2] =\int (x-\mu)^2 f(x) dx \ \bigl( = \sum_i(x_i-\mu)^2p_i \bigr)](images/EXTERN_0021.png)
と定義される.
また,σ を標準偏差(SD : Standard Deviation)といい,平均と同じ次元で分布の拡がりの大きさを表す量である.
積率母関数
確率変数 X の関数 exp(tX ) の期待値
![m(t) ={\rm E}[ e^{tX}] = \int e^{tx} f(x) dx \ \bigl( = \sum_i e^{tx_i}p_i \bigr)](images/EXTERN_0022.png)
を積率母関数(moment generating function)という.積率母関数を t で r 回微分すると,
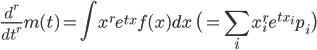
となるので,t → 0,とすれば,
![\frac{d^r}{dt^r}m(0)=\int x^r f(x) dx \ \bigl( = \sum_i x_i^r p_i \bigr) = {\rm E}[X^r]](images/EXTERN_0024.png)
となり,確率変数 X の r 次の積率(moment)E[X r] が比較的簡単に求まる.
2.統計的独立
独立
2つの確率変数
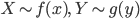
に対し,その同時分布(joint distribution)の密度関数を
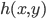
とする.
X と
Y が互いに独立(independent)であるのは,同時分布が
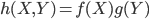
と変数分離される場合である.
独立な確率変数の平均と分散
2つの独立な確率変数 X,Y の平均と分散がそれぞれ,
であるとき,
![{\rm E}[X + Y] = {\rm E}[X] + {\rm E}[Y] = \mu_x + \mu_y, \ {\rm Var}[X+Y] ={\rm Var}[X] +{\rm Var}[Y] = \sigma^2_x +\sigma^2_y](images/EXTERN_0028.png)
![{\rm E}[X - Y] = {\rm E}[X] - {\rm E}[Y] = \mu_x + \mu_y, \ {\rm Var}[X-Y] ={\rm Var}[X] +{\rm Var}[Y] = \sigma^2_x +\sigma^2_y](images/EXTERN_0029.png)
である.一般に,スカラー a,b に対して
![{\rm E}[aX+bY]=a{\rm E}[X] + b{\rm E}[Y]=a\mu_x + b\mu_y, \ {\rm Var}[aX+bY]=a^2{\rm Var}[X] + b^2{\rm Var}[Y]=a^2 \sigma^2_x + b^2\sigma^2_y](images/EXTERN_0030.png)
である.
無作為標本
分布
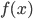
から大きさ n の標本
X1,…,
Xn を抽出したとき,それらが互いに独立であればその同時分布は
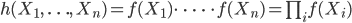
と因数分解される.このような標本を無作為標本(random sample)という. また,標本全体を母集団(population)といい,
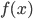
を母集団分布ともいう.母集団分布の平均や分散などを母集団母数(parameter)という.
大数の法則
平均が μ である分布をもつ母集団から大きさ n の無作為標本 X1,…,Xn を抽出したときに,
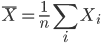
を標本平均(sample mean)という.このとき,標本の大きさ(サンプルサイズ(sample size))n を大きくしていくと,標本平均
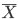
は母集団平均 μ に近づく(確率収束する).すなわち,どんな小さな正の数 ε に対して,
![{\rm Pr}[ | \bar{X} - \mu| \ > \ \epsilon ] \to 0, \ n \to \infty](images/EXTERN_0034.png)
が成り立つ.これを大数の法則(law of large numbers)という.
大数の法則は,母集団からたくさんの標本を取れば取るほど,より正確に母集団分布についての推論が行えることを保証している.また,母集団分布に従う乱数が正しく生成できるならば,コンピュータシミュレーションにより母集団母数ははぼ正確に求めることができる.さらに,母集団分布に従う乱数で生成される経験分布関数は,母集団分布関数に近づいていく.



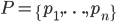 の中で,
の中で,
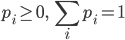
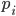 を確率密度(probability density)という.なお,
を確率密度(probability density)という.なお,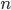 は可算無限(自然数と対応づけられる)であるならば離散的である.
は可算無限(自然数と対応づけられる)であるならば離散的である.
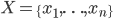 のおのおのの値に対し,それが生起する確率
のおのおのの値に対し,それが生起する確率 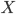 を離散確率変数(discrete random variable)という.これは,
を離散確率変数(discrete random variable)という.これは,
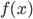 が,
が,
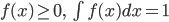
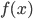 を確率密度関数(probability density function)とも呼ぶ.なお,確率密度関数
を確率密度関数(probability density function)とも呼ぶ.なお,確率密度関数 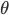 を持つとき,
を持つとき,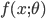 と表記することもある.
と表記することもある.
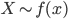 ,と表記する.
,と表記する.
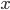 以下である確率,
以下である確率,
![F(x) = {\rm Pr}[X \le x] =\int_{-\infty}^x f(t)dt](images/EXTERN_0013.png)
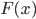 を累積分布関数(cumulative distribution function)という.この関数を用いると,確率変数
を累積分布関数(cumulative distribution function)という.この関数を用いると,確率変数 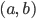 に落ちる確率は,
に落ちる確率は,
![{\rm Pr}[a <X\le b]=\int^a_b f(x)dx = F(b)-F(a)](images/EXTERN_0016.png)
![\mu={\rm E}[X] = \int xf(x) dx \ \bigl(=\sum_ix_ip_i \bigr)](images/EXTERN_0017.png)
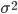 は,分布の拡がり(dispersion)の程度を表す.確率変数
は,分布の拡がり(dispersion)の程度を表す.確率変数 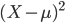 の期待値でもあり,
の期待値でもあり,
![\sigma^2 = {\rm Var}[X] ={\rm E}[(X-{\rm E}[X])^2] ={\rm E}[X^2] -({\rm E}[X])^2](images/EXTERN_0020.png)
![= {\rm E}[(X-\mu)^2] =\int (x-\mu)^2 f(x) dx \ \bigl( = \sum_i(x_i-\mu)^2p_i \bigr)](images/EXTERN_0021.png)
![m(t) ={\rm E}[ e^{tX}] = \int e^{tx} f(x) dx \ \bigl( = \sum_i e^{tx_i}p_i \bigr)](images/EXTERN_0022.png)
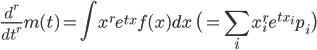
![\frac{d^r}{dt^r}m(0)=\int x^r f(x) dx \ \bigl( = \sum_i x_i^r p_i \bigr) = {\rm E}[X^r]](images/EXTERN_0024.png)
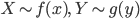 に対し,その同時分布(joint distribution)の密度関数を
に対し,その同時分布(joint distribution)の密度関数を 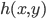 とする. X と Y が互いに独立(independent)であるのは,同時分布が
とする. X と Y が互いに独立(independent)であるのは,同時分布が
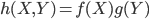
![{\rm E}[X + Y] = {\rm E}[X] + {\rm E}[Y] = \mu_x + \mu_y, \ {\rm Var}[X+Y] ={\rm Var}[X] +{\rm Var}[Y] = \sigma^2_x +\sigma^2_y](images/EXTERN_0028.png)
![{\rm E}[X - Y] = {\rm E}[X] - {\rm E}[Y] = \mu_x + \mu_y, \ {\rm Var}[X-Y] ={\rm Var}[X] +{\rm Var}[Y] = \sigma^2_x +\sigma^2_y](images/EXTERN_0029.png)
![{\rm E}[aX+bY]=a{\rm E}[X] + b{\rm E}[Y]=a\mu_x + b\mu_y, \ {\rm Var}[aX+bY]=a^2{\rm Var}[X] + b^2{\rm Var}[Y]=a^2 \sigma^2_x + b^2\sigma^2_y](images/EXTERN_0030.png)
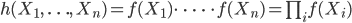
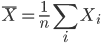
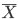 は母集団平均 μ に近づく(確率収束する).すなわち,どんな小さな正の数 ε に対して,
は母集団平均 μ に近づく(確率収束する).すなわち,どんな小さな正の数 ε に対して,
![{\rm Pr}[ | \bar{X} - \mu| \ > \ \epsilon ] \to 0, \ n \to \infty](images/EXTERN_0034.png)