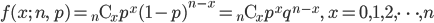
| 変数 X | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 確率 P | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
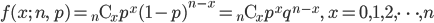
![m(t) ={\rm E}[e^{tX}]=\sum_x e^{tx} {}_n {\rm C}_x p^xq^{n-x} =\sum_x {}_n {\rm C}_x (pe^t )^xq^{n-x}=(pe^t + q)^n](images/EXTERN_0001.png)
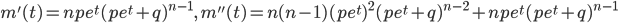
![{\rm E}[X]=m'(0)=np](images/EXTERN_0003.png) ,分散:
,分散:![{\rm Var}[X]=m''(0)-(np)^2=n(n-1)p^2+np-(np)^2=np(1-p)=npq](images/EXTERN_0004.png)
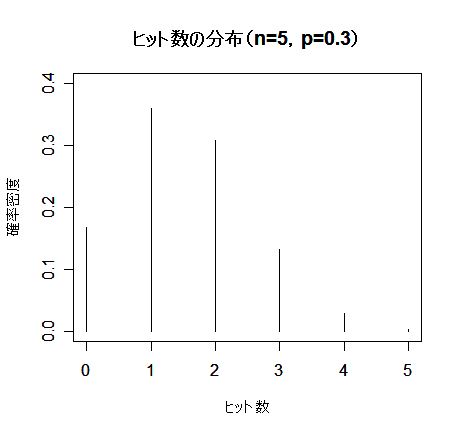
| n <- 5 | #試行回数 |
| x <- 0:n | #回数 |
| p <- 0.3 | #成功確率 |
| hit <- dbinom(x, size=n, prob=0.3) | #二項確率 |
| plot(x, hit, type="h", ylim=c(0,0.4), xlim=c(0,n), cex.lab=0.8, xlab="ヒット数", ylab="確率密度") | |
| title(main="ヒット数の分布(n=5,p=0.3)") | #タイトル |
| sum(x*hit) | #平均(np = 1.5) |
| sum(hit*(x - n*p)^2) | #分散(np(1 - p) = 1.05) |
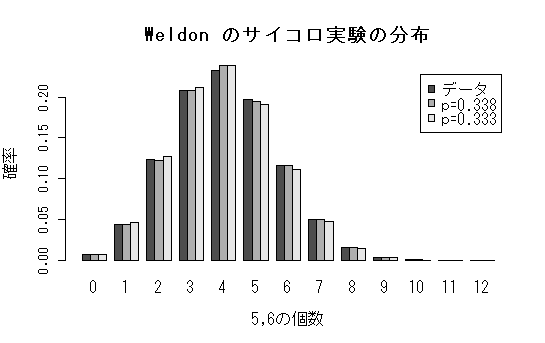
| 5,6の個数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| 出た回数 | 185 | 1149 | 3265 | 5475 | 6114 | 5194 | 3067 |
| 5,6の個数 | 7 | 8 | 9 | 10 | 11 | 12 | 合計 |
| 出た回数 | 1331 | 403 | 105 | 18 | 0 | 0 | 26306 |
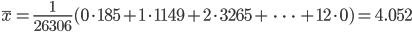 ,
,
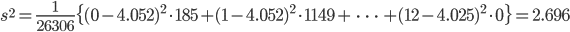
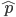 は,データの平均値を用いて,
は,データの平均値を用いて,
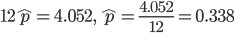
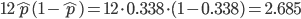
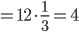 ,分散
,分散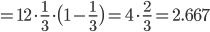
| モデル | 平均 | 分散 |
|---|---|---|
| データ | 4.052 | 2.696 |
| 二項分布(p=0.338) | 4.052 | 2.685 |
| 二項分布(p=0.333) | 4 | 2.667 |
| x <- 0:12 | #個数 |
| dice <- c(185,1149,3265,5475,6114,5194,3067,1331,403,105,18,0,0) | #回数データ |
| sum(dice) | #試行回数 |
| pdice <- dice/sum(dice) | #回数の確率 |
| m <- sum(x*pdice) | #平均 |
| p <- m/12 | #5,6の出る確率 |
| s2 <- sum(pdice*(x-m)^2) | #分散 |
| v <- 12*p*(1-p) | #二項分布のもとでの分散 |
| h1 <- dbinom(x, 12, 1/3) | #正しいサイコロのもとでの二項確率分布 |
| h2 <- dbinom(x, 12, p) | #推定確率からの二項確率分布 |
| dicedis <- rbind(pdice,h2,h1) | #行ベクトル->行列 |
| colnames(dicedis) <- as.character(0:12) | #列の名前 |
| barplot(dicedis, beside=TRUE, cex.axis=0.8, cex.lab=1.0, xlab="5,6の個数", ylab="確率", legend=c("データ","p=0.338", "p=0.333")) | |
| title(main="Weldon のサイコロ実験の分布") | #グラフタイトル |
| 女児数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| 度数 | 7 | 45 | 181 | 478 | 829 | 1112 | 1343 |
| 女児数 | 7 | 8 | 9 | 10 | 11 | 12 | 合計 |
| 度数 | 1033 | 670 | 286 | 104 | 24 | 3 | 6155 |
成功確率を p とし,0 以上の整数 X に対し,確率密度が,
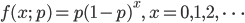
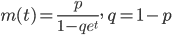
![{\rm E}[X] = \frac{q}{p} = \frac{1-p}{p}, \ {\rm Var}[X] = \frac{q}{p^2}=\frac{1-p}{p^2}](images/EXTERN_0014.png)
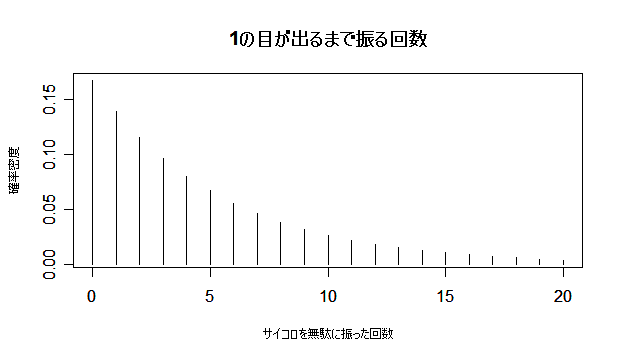
| x <- 0:100 | #本当は無限大まで必要(永遠に1が出ない) |
| p <- 1/6 | #成功確率 |
| y <- dgeom(x, p) | #幾何分布の確率密度) |
| # x は 0 から 20 まで表示 | |
| plot(x, y, type="h", cex.lab=0.8, xlim=c(0,20), xlab="サイコロを無駄に振った回数", ylab="確率密度") | |
| title(main="1 の目が出るまで振る回数の分布") | #タイトル |
| sum(x*y) | #平均((1 - p)/p = (5/6)/(1/6) = 5) |
| sum(y*(x - (1-p)/p)^2) | #分散((1 - p)/p2 = (5/6)/(1/36) = 30) |
m 個の白石と n 個の黒石が入った袋から k 個の石を無作為に取り出したとき,
白石の個数 X の従う確率密度は,
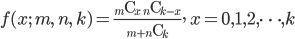
![{\rm E}[X]=kp](images/EXTERN_0016.png) ,分散:
,分散:![{\rm Var}[X]=kp(1-p)(m+n-k), \ p=\frac{m}{m+n}](images/EXTERN_0017.png)
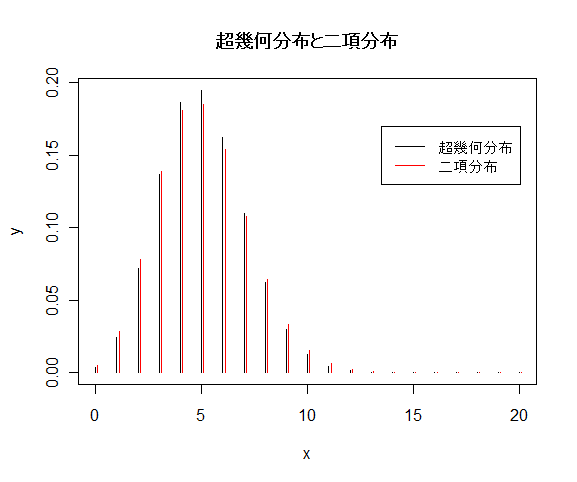
| x <- 0:20 | # 抽出された白石の個数 |
| m <- 50 | # 白石の個数 |
| n <- 450 | # 黒石の個数 |
| k <- 50 | # 抽出回数 |
| y <- dhyper(x, m, n, k) | # 超幾何分布確率分布 |
| plot(x,y,type="h") | # |
| p <- m/(m+n) | # 白石が選ばれる確率 |
| yd <- dbinom(x, k, p) | # 二項確率 |
| x1 <- x+0.1 | # 0.1 ずらして表示 |
| points(x1, yd, type="h", col="red") | # 二項確率のグラフ |
| title(main="超幾何分布と二項分布") | # |
| legend(locator(1),c("超幾何分布","二項分布"), lty=1, col=c("black", "red")) | |
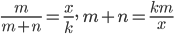
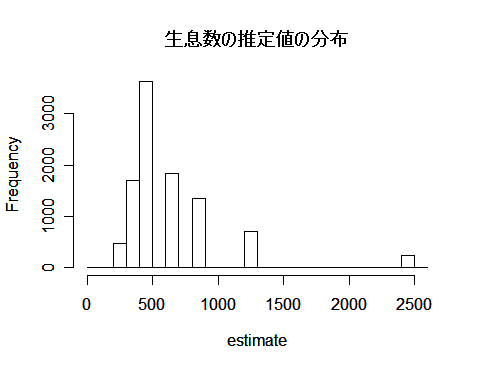
m <- 50 # 標識をつけた数
n <- 450 # 標識をつけられていない数
k <- 50 # 再捕獲数
estimate <- NULL # 個体数推定値の定義
for (i in 1:10000) { # 10000回のシミュレーション
x <- rhyper(1, m, n, k) # 超幾何分布に従う乱数1つ抽出
estimate <- c(estimate, k * m / x) # 個体数推定値列ベクトル
} #
hist(estimate, breaks=seq(0, 2600, by=100), main="") #推定値のヒストグラム
title(main="生息数の推定値の分布") #タイトル
table(estimate) #推定値の階級分け
quantile(estimate, c(0.05, 0.1, 0.5, 0.9, 0.95)) # 分位点(パーセンタイル)
|
課題:上の例では捕獲(m = 50),再捕獲(k = 50)合わせて 100頭を捕獲している. 捕獲数を半分にした場合の生息数の推定精度はどうなるか.m や k を適当に動かしてみて調べよ.
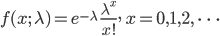
![m(t)={\rm E}[e^{tX}]= \sum^\infty_{x=0} \frac{e^{tx}e^{-\lambda}\lambda^x}{x!} = e^{-\lambda} \sum^\infty_{x=0} \frac{(\lambda e^t)^x}{x!} = e^{-\lambda} e^{\lambda e^t}](images/EXTERN_0020.png)
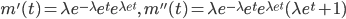
![{\rm E}[X] = m'(0)=\lambda](images/EXTERN_0022.png) ,
,
![{\rm Var}[X]={\rm E}[X^2] - ({\rm E}[X] )^2 = m''(0)-\lambda^2 = \lambda(\lambda+1)-\lambda^2=\lambda](images/EXTERN_0023.png)
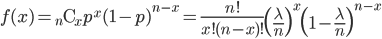
![= \frac{\lambda^x}{x!} \Bigl[ \bigl(1- \frac{1}{n} \big) \cdot \ \cdots \ \cdot \bigl( 1- \frac{n-1}{n} \bigr) \Bigr] \bigl(1-\frac{\lambda}{n} \bigr)^{-x} \bigl(1-\frac{\lambda}{n} \bigr)^n](images/EXTERN_0025.png)
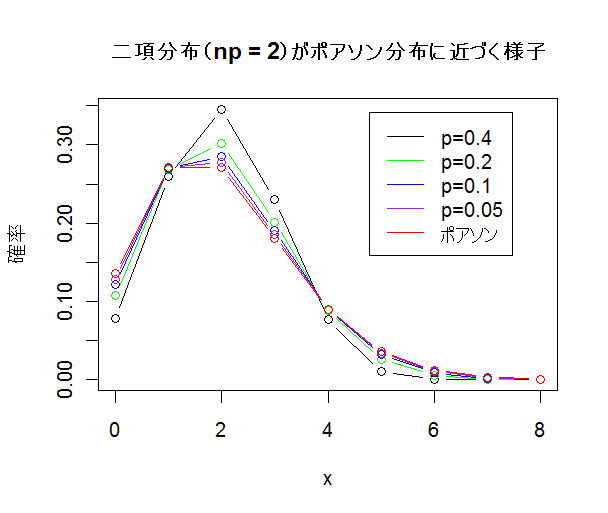
| x <- 0:8 | #グラフのx軸の範囲 |
| lam <- 2 | #λの定義 |
| yp <- dpois(x,lam) | #ポアソン分布の確率密度 |
| y1 <- dbinom(x, 5, 0.4) | #二項分布(n = 5,p = 0.4)の確率密度 |
| y2 <- dbinom(x, 10, 0.2) | #二項分布(n = 10,p = 0.2)の確率密度 |
| y3 <- dbinom(x, 20, 1/10) | #二項分布(n = 20,p = 0.1)の確率密度 |
| y4 <- dbinom(x, 40, 1/20) | #二項分布(n = 40,p = 0.05)の確率密度 |
| plot(x, y1, type="b", ylab="確率") | #二項分布(n = 5,p = 0.4)のプロット(黒) |
| points(x, y2, type="b", col="green") | #二項分布(n = 10,p = 0.2)のプロット(赤) |
| points(x, y3, type="b", col="blue") | #二項分布(n = 20,p = 0.1)のプロット(青) |
| points(x, y4, type="b", col="purple") | #二項分布(n = 40,p = 0.05)のプロット(紫) |
| points(x, yp, type="b", col="red") | #ポアソン分布のプロット(赤) |
| title(main="二項分布(np = 2)がポアソン分布に近づく様子") | |
| # 凡例の記述(locator(1)は,凡例の記述場所をクリックで指定) | |
| legend(locator(1), c("p=0.4", "p=0.2", "p=0.1", "p=0.05", "ポアソン"), | |
| lty=1, col=c("black", "green", "blue", "purple", "red")) | |
| 死亡記事件数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 以上 |
|---|---|---|---|---|---|---|---|
| 日数 | 484 | 391 | 164 | 45 | 11 | 1 | 0 |
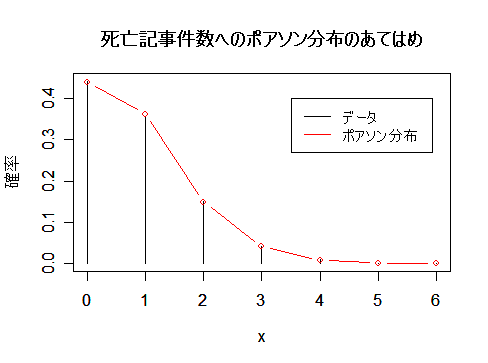
死亡記事件数データの平均は0.8239,分散は0.8294,であった.このデータがポアソン分布に従っている
と考える.ポアソン分布の平均は λ なので,λ = 0.8239 のポアソン分布にあてはめてみたところ,非常によく
一致していた.
また,ポアソン分布は,平均と分散が等しいという特徴がある.データの平均と分散の値が
近いことから,データはポアソン分布によく適合していることを示している.
 |
|
| x <- 0:6 | #グラフのx軸の範囲 |
| y <- c(484, 391, 164, 45, 11, 1, 0) | #死亡記事件数データ |
| s <- sum(y) | #データ総数 |
| m <- sum(x*y/s) | #データ分布の平均 |
| v <- sum((x-m)^2*y/s) | #データ分布の分散 |
| yp <- dpois(x, m) | #平均 m のポアソン分布確率密度 |
| plot(x, y/s, type="h", ylab="確率") | #データの棒グラフ表示 |
| points(x, yp, type="b", col="red") | #ポアソン分布の重ねがき(赤) |
| title(main="死亡記事件数へのポアソン分布のあてはめ") | |
| legend(3.5, 0.4, c("データ", "ポアソン分布"), lty=1, col=c("black","red")) | |
7 日間で売れる商品の個数は,平均 2×7 = 14 のポアソン分布に従うと考えられる.ポアソン分布 の95%(分位)点を求めればよい.これより,必要な在庫は20個とわかる.
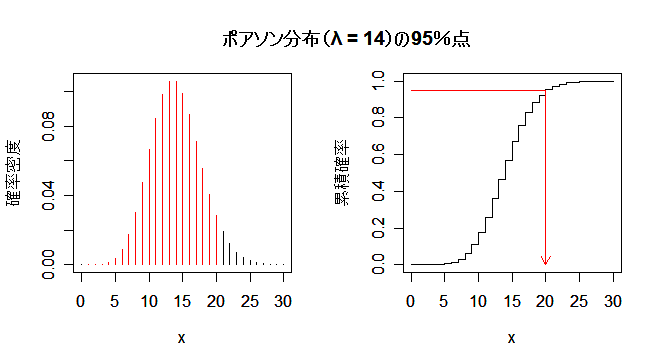
| m <- 14 | # ポアソン分布のパラメータ(平均) |
| x <- 0:30 | # グラフのx軸の範囲 |
| yp <- dpois(x, m) | # ポアソン分布確率密度 |
| cyp <- ppois(x,m) | # ポアソン分布累積確率 |
| stok <- qpois(0.95, m) | # 95%(分位)点 |
| stok | # 答えの表示 |
| op <- par(mfrow = c(1, 2)) | # 横に2つのグラフを並べる |
| plot(x, yp, type="h", ylab="確率密度") | # 確率密度グラフ |
| points(x[2:21],yp[2:21], type="h", col="red") | # x = 20 まで赤色表示 |
| plot(x,cyp,type="s", ylab="累積確率") | # 累積確率グラフ |
| arrows(stok,0.95,stok,0, length=0.1, col="red") | # 赤矢印 |
| segments(0,0.95, stok,0.95, col="red") | # |
| par(op) | # グラフ表示もとに戻す |
| title(main="ポアソン分布(λ = 14)の95%点") | # グラフタイトル |
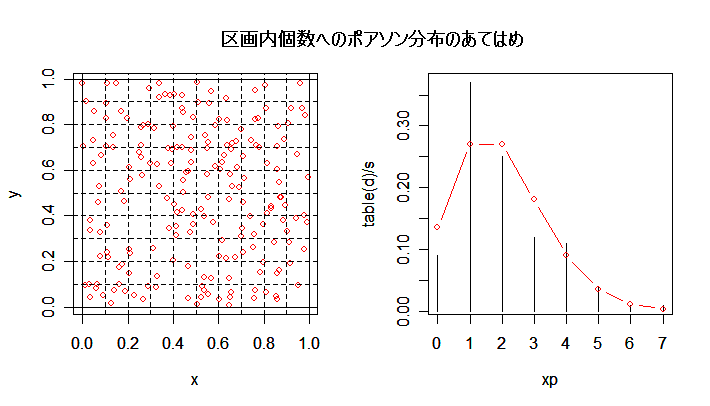
| n <- 200 | # 個体数 |
| m <- 10 | # メッシュ(m2 個) |
| x <- runif(n) | # 一様乱数n個 |
| y <- runif(n) | # 一様乱数n個 |
| # | # |
| count <- NULL | # count の定義 |
| for(i in 1:m){ | # m 回の繰り返し |
| n1 <- (1:n)[x < (i-1)/m] | # (i-1)/m 以下の乱数である番号 |
| n2 <- (1:n)[x < i/m] | # i/m 以下の乱数である番号 |
| nin <- n2[!n2 %in% n1] | # (i-1)/m から i/m の番号 |
| yy <- y[nin] | # 上記 x 座標に対する y 座標 |
| a <- hist(yy, breaks=0:m/m) | # yy を 0 から 1 まで 1/m きざみで区切る |
| count <- c(count, a$counts) | # 区切った領域に入った個体の個数のベクトル |
| } | # 繰り返しここまで |
| mc <- max(count) | # メッシュ内の個数の最大値 |
| xp <- 0:mc | # 個数の定義域 |
| d <- factor(count, levels=xp) | # 個数が 0 の階級も含める |
| table(d) | # メッシュ内個数の区分 |
| s <- sum(table(d)) | # 総個数 |
| m1 <- sum(xp*table(d)/s) | # カウント分布の平均 |
| m2 <- mean(count) | # カウントデータの標本平均 |
| v1 <- sum(table(d)/s*(xp-m1)^2) | # カウント分布の分散 |
| v2 <- var(count) | # カウントデータの標本分散 |
| # | # |
| op <- par(mfrow = c(1, 2)) | # 横に2つのグラフを並べる |
| plot(x,y, col="red") | # 個体分布の表示 |
| abline(h=0, v=0) | # 外枠 |
| abline(h=1, v=1) | # 外枠 |
| for(i in 1:m) abline(h=i/m, v=i/m, lty=2) | # メッシュ区分線 |
| plot(xp, table(d)/s, type="h") | # 区分された分布のグラフ |
| lam <- n/(m*m) | # 平均 |
| yp <- dpois(xp, lam) | # ポアソン分布確率密度 |
| points(xp, yp, type="b", col="red") | # ポアソン分布グラフ表示 |
| par(op) | # グラフ表示もとに戻す |
| title(main="区画内個体数へのポアソン分布のあてはめ(平均:2)") | # タイトル |
| m1 | # カウント分布平均 |
| v1 | # カウント分布分散 |
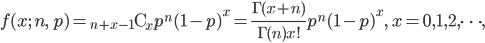
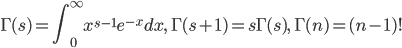
![m(t) = {\rm E}[e^{tX}] = \sum_{x=0}^{\infty} e^{tx} {-r \choose x}p^n(-q)^x = \sum_{x=0}^{\infty} {-r \choose x}p^n(-qe^t)^x = \left(\frac{p}{1-qe^t} \right)^n](images/EXTERN_0029.png)
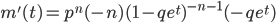
![m''(t)=nqp^n [q(n+1)e^{2t}(1-qe^t)^{-n-2} + e^t (1-qe^t)^{-n-1} ]](images/EXTERN_0031.png)
![{\rm E}[X] = m'(0) = \frac{nq}{p}](images/EXTERN_0032.png)
![{\rm Var}[X] = {\rm E}[X^2] -({\rm E}[X])^2 = m''(0)-\Bigl( \frac{nq}{p} \Bigr)^2](images/EXTERN_0033.png)
![=nqp^n[qp^{-n-2}(n+1)+p^{-n-1}] - \Bigl(\frac{nq}{p} \Bigr)^2 = \frac{nq^2}{p^2} + \frac{nq}{p} = \frac{nq}{p^2}](images/EXTERN_0034.png)
| 虫歯の数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| 児童の数 | 4 | 9 | 16 | 13 | 9 | 7 | 5 | 4 | 3 |
虫歯数データが負の二項分布に従っていると仮定する.虫歯データの平均は3.3286,分散は4.3063,
であった.負の二項分布は2つのパラメータ n,p を持つのでそれをデータから推定する必要がある.
分布パラメータの推定法は後に詳しく議論するが,ここでは直感的に理解しやすいモーメント法を説明
する.これは,分布の平均や分散などのモーメントがデータの平均や分散と等しい,とおくことでパラメータ
の推定を行う方法である.
課題:負の二項分布の確率密度は dnbinom(x, n, p) で与えられる.モーメント法を用いてパラメータ n,p の値を推定し,この推定値を用いて,児童の虫歯データに負の二項分布をあてはめたグラフ (下図のようなもの)を描け.
モーメント法による推定値を用いて,虫歯数データに負の二項分布をあてはめた.データは分布にまあまあ 適合しているようにみえる.
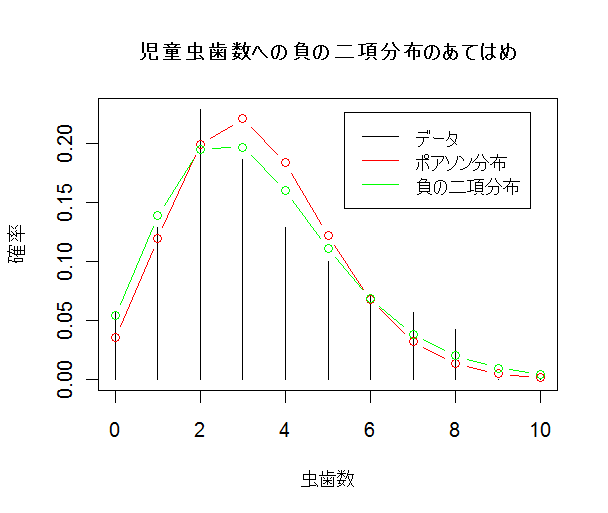
| x <- 0:10 | #グラフのx軸の範囲 |
| y <- c(4,9,16,13,9,7,5,4,3,0,0) | #虫歯数 |
| s <- sum(y) | #虫歯数の総和 |
| m <- sum(x*y/s) | #平均 |
| v <- sum((x-m)^2*y/s) | #分散 |
nbp <- m/v #
nbn <- m*nbp/(1-nbp)
plot(x, y/s, type="h", xlab="虫歯数", ylab="確率")
yp <- dpois(x, m)
points(x, yp, type="b", col="red")
ynb <- dnbinom(x, nbn, nbp)
points(x, ynb, type="b", col="green") # 負の二項分布表示
legend(locator(1), c("データ", "ポアソン分布", "負の二項分布"),
lty=1, col=c("black","red","green"))
title(main="児童虫歯数への負の二項分布のあてはめ")
|
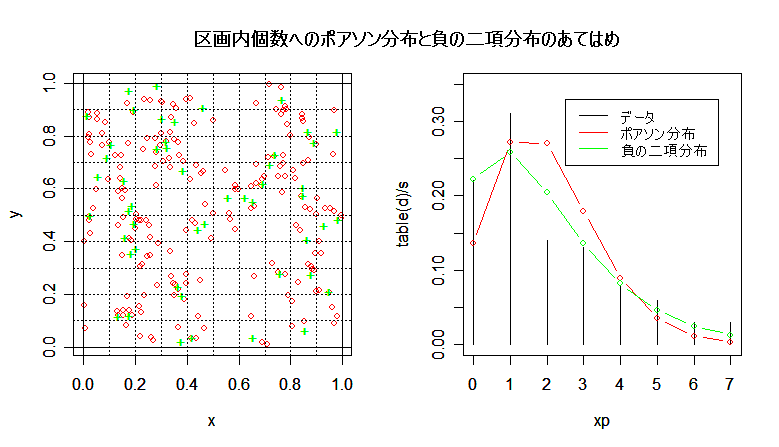
| n <- 200 | # 個体数(予定) |
| m <- 10 | # メッシュ(m2 個) |
| p <- 4 | # 平均子ども数 |
| sig <- 0.05 | # 正規分布標準偏差 |
| xx <- NULL | # xx(子ども座標)の定義 |
| xx0 <- NULL | # xx0(親座標)の定義 |
| np <- round(n/p) | # 親の数(round() は 5 捨 6 入) |
| for(i in 1:np){ | # np 回の繰り返し |
| x0 <- runif(2) | # 親個体の座標を一様乱数で生成 |
| n0 <- rpois(1, p) | # 子どもの数を平均 p のポアソン乱数で生成 |
| for(j in 1:n0){ | # n0 回の繰り返し |
| xd <- rnorm(2, m=x0, sd=sig) | # 子どもの座標を,正規乱数 N(x0, sig2)で生成 |
| if(xd[1] > 1) xd[1] <- xd[1] - 1 | # x 座標が 1 を超えたとき区画の左端に |
| if(xd[1] < 0) xd[1] <- xd[1] + 1 | # x 座標が 0 未満のとき区画の右端に |
| if(xd[2] > 1) xd[2] <- xd[2] - 1 | # y 座標が 1 を超えたとき区画の下辺に |
| if(xd[2] < 0) xd[2] <- xd[2] + 1 | # y 座標が 0 未満のとき区画の上辺に |
| xx <- rbind(xx, xd) | # 個体座標行列の行の追加 |
| xx0 <- rbind(xx0, x0) | # 個体座標行列の行の追加 |
| } | # |
| } | # |
| # 区画内個体数 | # |
| x <- xx[,1]; y <- xx[,2] | # x 座標ベクトル,y 座標ベクトル |
| count <- NULL | # count の定義 |
| for(i in 1:m){ | # m 回の繰り返し |
| n1 <- (1:n)[x < (i-1)/m] | # (i-1)/m 以下の乱数である番号 |
| n2 <- (1:n)[x < i/m] | # i/m 以下の乱数である番号 |
| nin <- n2[!n2 %in% n1] | # (i-1)/m から i/m の番号 |
| yy <- y[nin] | # 上記 x 座標に対する y 座標 |
| a <- hist(yy, breaks=0:m/m) | # yy を 0 から 1 まで 1/m きざみで区切る |
| count <- c(count, a$counts) | # 区切った領域に入った個体の個数のベクトル |
| } | # |
| mc <- max(count) | # メッシュ内の個数の最大値 |
| xp <- 0:mc | # 個数の定義域 |
| d <- factor(count, levels=xp) | # 個数が 0 の階級も含める |
| table(d) | # メッシュ内個数の階級区分 |
| s <- sum(table(d)) | # 総個体数 |
| m1 <- sum(xp*table(d)/s) | # カウント分布の平均 |
| v1 <- sum(table(d)/s*(xp-m1)^2) | # カウント分布の分散 |
| # | # |
| op <- par(mfrow = c(1, 2)) | # 横に2つのグラフを並べる |
| plot(x,y, col="red") | # 個体分布の表示 |
| points(xx0, pch="+", col="green") | # 個体分布の表示 |
| abline(h=0, v=0) | # 外枠 |
| abline(h=1, v=1) | # 外枠 |
| for(i in 1:m) abline(h=i/m, v=i/m, lty=3) | # メッシュ区分線 |
| plot(xp, table(d)/s, type="h", ylim=c(0,0.35)) | # 区分された分布のグラフ |
| yp <- dpois(xp, m1) | # ポアソン分布確率 |
| points(xp, yp, type="b", col="red") | # ポアソン分布表示 |
| nbp <- m1/v1 | # |
| nbn <- m1*nbp/(1-nbp) | # |
| ynb <- dnbinom(xp, nbn, nbp) | # 負の二項分布確率 |
| points(xp, ynb, type="b", col="green") | # 負の二項分布表示 |
| legend(2.5, 0.33, c("データ", "ポアソン分布", "負の二項分布"), lty=1, col=c("black","red","green")) | |
| par(op) | # 個体数 |
| title(main="区画内個数へのポアソン分布と負の二項分布のあてはめ") | |
| m1 | # 平均 |
| v1 | # 分散 |
| データ | 適応する分布 | 平均 | 分散 |
|---|---|---|---|
| 平均>分散 | 二項分布 | np | np(1 - p) |
| 平均≒分散 | ポアソン分布 | λ | λ |
| 平均<分散 | 負の二項分布 | n(1 - p)/p | n(1 - p)/p2 |